1.2: The Nature of Time

Spacetime Events

We now embark on deriving the consequences of the relativity principle in the same way that Einstein did – using a tool he called Gedankenexperiment (thought experiment). in order to keep everything straight in our discussions, we begin by defining a spacetime event.

In the context of special relativity, a spacetime event is an instantaneous occurrence at a specific point in space and at a specific moment in time. A single point on a stationary light bulb as it dims defines a specified location, but it is not an event because the dimming process does not occur at a single instant in time. A baseball bat at exactly 12:01pm occurs at a single instant in time, but it is not an event, because the position is not specified at a single point. An easy way to visualize a spacetime event is to picture it as a very quick flash of light from a point source. The position of the point source and the instant in time the flash occurs define the space and time “coordinates” of the spacetime event.

It is much easier to define what a spacetime event is than it is to put physical quantities in terms of the spacetime coordinates, but as we will see, this is exactly what we will have to do to make sense of what is to come. We begin with one of most startling results, which is ironically one of the easiest to derive.

Time Dilation

Our first thought experiment involves turning the function of a clock into a series of spacetime events. This clock functions as follows: Light bounces back-and-forth between two mirrors, and every time it strikes one of the mirrors, the clock "ticks." We begin with Ann's perspective on what is happening with this clock. She happens to be in the same frame as the two mirrors, so to her they are at rest, and the light is bouncing parallel to her \(y\)-axis. The two spacetime events we will look at are two consecutive ticks of the clock.

Figure 1.2.1 – Ann's Perspective of the Light Clock

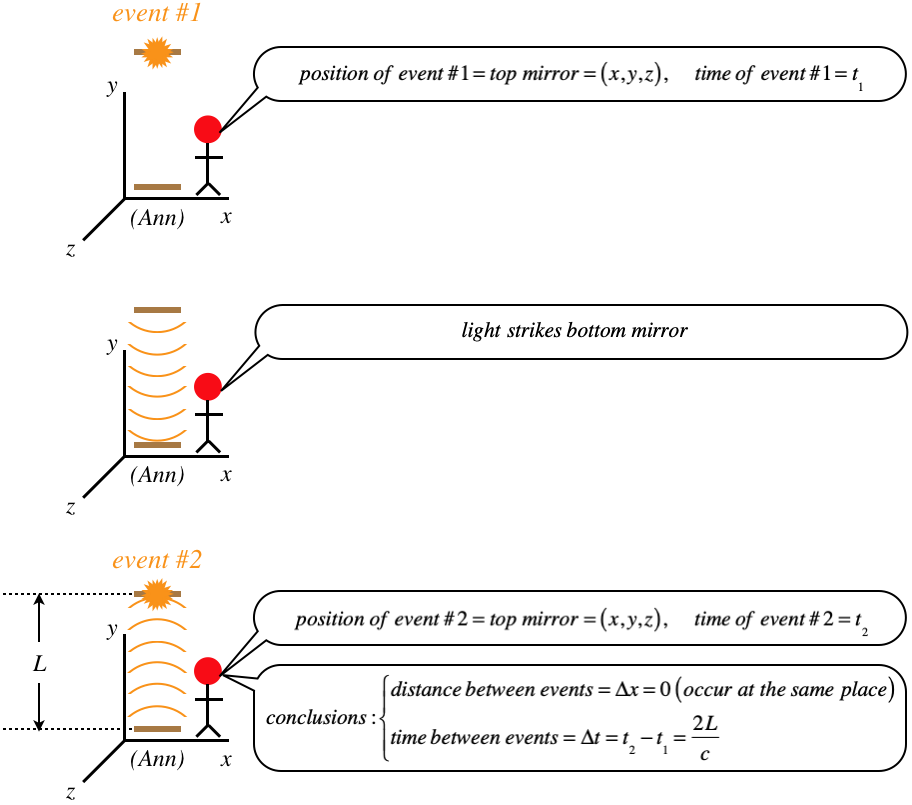
Okay, so we have used the two events to determine the time span between them according to Ann. The goal of relativity is to describe what a second observer measures for a physical process given what the first observer measured. So now we introduce Bob, who is in what we call the primed inertial frame, moving at a constant speed \(v\) in the \(+x\)-direction relative to Ann. One might interject, "Wait, this is time we are talking about! Won't both of them measure the same amount of time between ticks of the clock?" Don't assume anything in relativity – just use the spacetime events and the postulate(s), and see where it leads.

Looking from Bob's perspective means that not only is Ann moving in the \(-x\)-direction, as we noted previously, but the two events (which both occur at the top mirror) don't occur at the same position in space, since the mirror moves:

Figure 1.2.2 – Bob's Perspective of the Light Clock

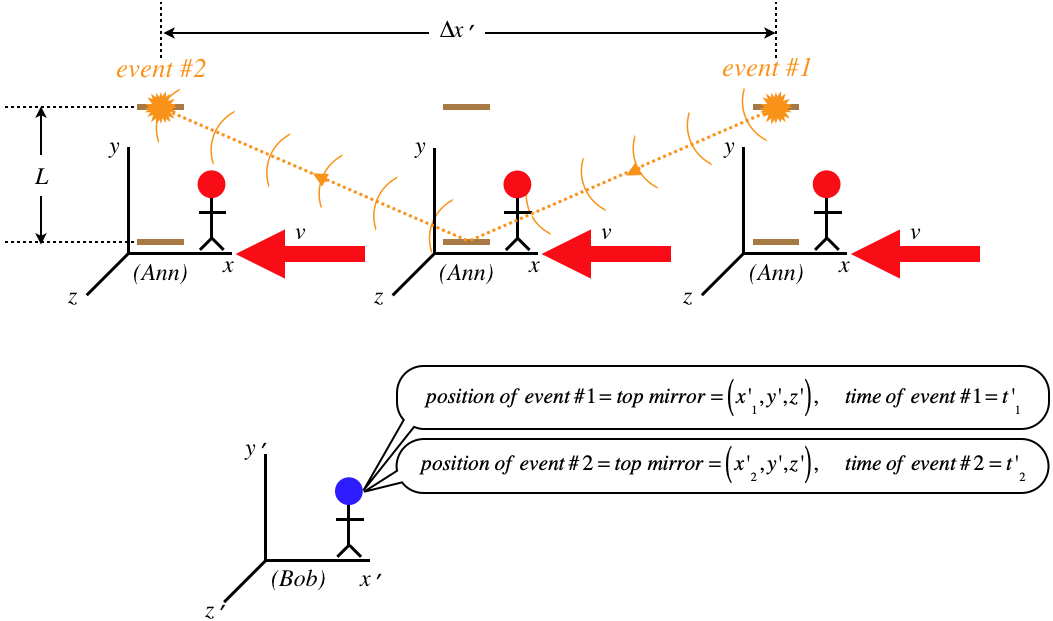
Now we calculate the time between the two events, as we did for Ann. From Bob's perspective, the light travels a longer distance than Ann measures, and very importantly, both Ann and Bob measure the speed of light to be the same (postulate of relativity), so Bob must measure a longer time period than Ann measures between the same ticks of the light clock! According to Bob, the light travels diagonally from the top mirror to the bottom one, and the length of this half of the trip can be written in terms of the speed of light, and in terms of the Pythagorean Theorem:

\[\begin{array}{l} \Delta x' = x'_2 - x'_1 = v\Delta t' \\ c\Delta t' = 2\sqrt{L^2+\left(\frac{\Delta x'}{2}\right)^2} \end{array}\]

We can eliminate \(\Delta x'\) from these two equations to relate the time span measured by Bob to the time span measured by Ann:

\[\Delta t' = \dfrac{1}{\sqrt{1-\frac{v^2}{c^2}}} \left(\dfrac{2L}{c}\right) = \gamma_v \Delta t \;,\;\;\; \gamma_v \equiv \dfrac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]

The time between ticks for Bob is greater than the time between ticks for Ann by a factor of \(\gamma_v\) (which is clearly a constant greater than 1). Just to clarify, this is not an optical illusion for Bob – he doesn't just "see the clock ticking slower than it really is," it is actually ticking slower. Also, it is important to note that while we used light to achieve this answer, it doesn't just apply to light phenomena, it applies to time flow in all its manifestations. If Ann measures her own pulse to be 60 beats per second (one second between each beat), and \(\gamma_v=2\), the Bob would measure Ann's heart rate to be 30 beats per second (2 seconds between each beat).

It's worth taking a moment to review what the source of this result is. It comes from the fact that the light in the light clock travels farther for Bob than it does for Ann, but they agree on the speed of that light, which means that the time between the two events must be greater for Bob than it is for Ann.

As startling as this result is, it gets weirder. Suppose Bob has a light clock exactly like Ann's. What does Ann observe when she looks at Bob's clock? She sees exactly the same thing happening with Bob's clock as he sees with her clock! Therefore Ann claims that time is passing slower for Bob than it is for her, even as Bob says that Ann's time is passing slower than his own. Which one of them is correct? Is Ann's time passing slower, or is Bob's? They are both in inertial frames, so according to the principle of relativity, each has an equal right to declare themselves to be "stationary." Therefore they are both right. The reason it seems like it is impossible that this can be true is that we cling to the incorrect notion that time is universal. The time span between two events is a relative quantity that depends upon who measures it.

Recording Spacetime Coordinates

While the calculation above is correct, it does require an assumption that we need to briefly address. Both Ann and Bob noted the positions and times of the events in their frames. Given the importance of both position and time in relativity, we need to be specific about how these numbers are recorded. What is observed is a spacetime event, which we have modeled as a flash of light that occurs in an instant at a specific position. So let's imagine constructing a massive lattice of labeled positions throughout all of space, and the position of any possible flash must coincide with one of those positions, giving us our spatial label. Note that every inertial observer can create such a lattice independent of every other observer, because according to the relativity principle, everyone has an equally valid claim to being "stationary."  It is true that Bob's lattice of position labels is moving according to Ann, but Ann and Bob only use their own stationary labels to describe the positions of events they see.

To get a complete reckoning of an event, we need to record not only its position, but the time at which it occurs.  Given what we know about the rate of time flow for moving clocks, we have to be very careful about how we measure the time at which an event occurs.  The one way to be safe is to have the clock that reads the time be positioned at the same place in space as the event. So whenever an event occurs, one simply reads the label of the lattice point at which it occurs, and the value indicated by a clock located at that lattice point when the event occurs.

Two Different Time Measurements

Now that we have a plan for recording data for events in spacetime, we need to give a little more thought to how we plan to have a clock that is properly positioned to measure the time.  It turns out that there are two fundamentally different ways to achieve this.

coordinate time

The first way that comes to mind for measuring the time of any given event is to simply place a separate clock at every lattice point. While this is a simple way to get a measurement for any event, we will be interested the time intervals between two events, which means that all of our clocks positioned throughout space need to be synchronized.  How do we do this?  If we bring all our clocks together in one place, set them the same, and then move them out to their assigned locations, then the weird effects that come from relative motion of clocks make un-synchronize them when they are moved. Instead what we can do is this

1. Distribute all of the clocks throughout space.
2. Set the clock at the origin to a time of 0:00.
3. Using the lattice positions of the clocks, compute the time it will take a spherical wave pulse of light that starts at the origin to reach all the other clocks, add this time to 0:00, and set the clock at this time.
4. Start the clock at the origin while starting the spherical pulse of light from the origin.
5. When the light wave reaches a clock, start it running.

Figure 1.2.3 – Synchronizing Clocks Distributed in Space

By anticipating what the time on the origin clock must be when the light arrives, we can assure that the spherical wave propagates clock synchronization throughout space.  This measurement of the time of an event is called coordinate time \(t\).

In the example above, both Ann and Bob measured the time between ticks in their own coordinate time. For Ann, the coordinate time span between the two spacetime events was \(\Delta t = t_2 - t_1\), while for Bob it was \(\Delta t' = t'_2 - t'_1\). As we found in the thought experiment, these values are not equal, which is to say that this manner of measuring a time span between two events is relative. Whenever the value of a physical quantity is different when measured from different inertial frames, we say that such a quantity is frame-dependent. We therefore declare:

Coordinate time spans are frame-dependent.

proper time

We certainly are not required to measure time between events by placing synchronized clocks at all the lattice points in our frame. Another way would be to use a single clock that is moved from the lattice point of the first event to the lattice point of the second. As before, a clock records the time of the event while it is at the same point in the lattice as the event, but this time it is the same clock, which means we do not need to rely upon our synchronization method above. A time interval measured in this manner is called a proper time \(\Delta \tau\) between the spacetime events.

Alert

The name "proper time" dates back to the early days of relativity, and is still used today, but it is dangerously misleading for those new to the subject. The word "proper" can easily be misconstrued to mean "correct," and hopefully this section is making it clear that this is cannot be the case. We are in the process of defining two different ways of measuring the time between two events (which can give different answers), and neither of these is any more correct than the other. The sooner the reader purges from their thoughts the notion that time is absolute and that there must be one correct value for the time between two events, the better.

It might seem like both the coordinate and proper time methods of measuring time intervals between events should produce the same result, but in fact they do not. The figures below demonstrates these two measurements for the same two spacetime events.

Figure 1.2.4 – Spacetime Events

Here we have just two spacetime events viewed from a particular reference frame.

Figure 1.2.5 – Coordinate Time Interval

These are the same two events, viewed from the same reference frame, but the coordinate time clocks placed at the positions of the events are in place to measure the times at which the events occur.

Figure 1.2.6 – Proper Time Interval

Again we have the same two spacetime events, viewed in the same frame, but a clock at rest in a different frame is now visible, and it measures the time interval between the two spacetime events, but in that frame the events occur at the same position (at the nose of the rocket ship).

Our example with Ann and Bob earlier shows why these time measurements come out different, if the postulate of special relativity about the constancy of the speed of light is accurate.  The two flashes occur at the same lattice point in Ann's frame (the top mirror remains at the same place in Ann's labeled lattice), so she measures the time interval using the proper time method.  Meanwhile, the top mirror moves from one lattice point in Bob's frame to another, so he relies upon the synchronized clocks positioned at those points for the time interval. The thought experiment demonstrates through the postulates of relativity that these two time intervals are not equal.

Example \(\PageIndex{1}\)

In the figures above that depict two spacetime events and a spaceship moving between them, we are observing from an inertial frame. How fast is the spaceship moving relative to this frame?

Solution

The two events occur at the same position in space in the ship's frame (at its nose - remember that the people on the ship can claim that the ship is not moving, so the two flashes occur at the same place). Therefore the ship measures the proper time interval between the two flashes, just as Ann measured the proper time interval of the two flashes at the top mirror.  Using the formula we derived to express the relationship between the time intervals, we find:

\[\Delta t= \gamma_v \Delta \tau \;\;\;\Rightarrow\;\;\; \sqrt{1-\frac{v^2}{c^2}}=\frac{\Delta \tau}{\Delta t}=\frac{12s}{15s}=0.8\;\;\;\Rightarrow\;\;\; v=0.6c\nonumber\]

The feature that best distinguishes proper time from coordinate time is the fact that a coordinate system is not needed to measure proper time. For example, we could introduce several other inertial frames of reference to look at the time interval between those top mirror flashes, but only Ann's clock will measure the time interval as the the one where the flashes occur at the same position in space – every frame other than Ann's will be similar to Bob's, in that the flashes occur at different lattice positions for their frame. All of the observers will agree on one thing – that Ann's measurement of the time interval is somehow "special", and this gives them a way to all agree upon a time interval.  Put another way, the measurement of proper time (essentially asking Ann what answer she got, as she was the only observer in an inertial frame to have both events occur at the same position) gives the same result for all reference frames. That is: 

Proper time is frame-independent.

Besides "frame-independent," a word typically used to describe a physical quantity like proper time that doesn't vary from one frame to another, is invariant.

Note that it is possible for a proper time measurement to be equal to a coordinate time measurement. For example, in the case discussed above, Ann sees the two events occur at the same lattice point in her frame, so if she looks at the clock placed there, it is the same clock measuring the time for both events, which means it also records the proper time. Bob's measurement of coordinate time, on the other hand, is not the proper time, since he reads the numbers off two different clocks – one placed at the lattice point of the first spacetime event, and one placed at the second. From the light clock example, it should be clear that the shortest distance the light has to travel between the two mirrors occurs in Ann's frame. That is, every frame other than the "proper frame" that measures coordinate time is going to measure a longer time interval between the events than the proper time.

two important notes

There are two details that have not been tied-up above that we will mention here and address in a future section:

1. The proper time between two events may not be definable as a real number, if the events are separated by a distance that is too great for the spaceship to cross in the interval between their occurrences.  For example, if the two events viewed in the frame of the figure above occurred simultaneously in that frame, then there is no way for the spaceship to traverse the distance between the events fast enough to allow both events to both occur at the nose of the ship.  We will see later that there is another invariant quantity that applies to any two events, and that the proper time interval is a special case of this invariant when an inertial frame exists that can measure the events at the same position in space.
2. We have defined the proper time here as being measured in an inertial frame, but the spaceship could also have both events occur at its nose when it accelerates between the two events.  This will come out to a different result than the inertial frame case, so it is important when declaring (as we did above) that the "proper time is frame-independent", that we keep in mind that this is restricted to the specific history of the clock that measures it.  That is, every observer will agree on the proper time measured by a single clock that is present at the positions of both events. "Invariance" pertains to different observers, not different clocks.  A second clock that is present at the positions of both events will not necessarily measure the same proper time interval as the first clock.  The way that each clock gets from the first event to the second (namely, its acceleration during the trip) determines how these two proper time measurements may differ.

Cosmic Speed Limit and the Spacetime Interval

When we look back at the time dilation result we obtained above, an obvious question comes to mind: If we observe a clock in a moving frame to tick more slowly than one in our rest frame by a factor of \(\sqrt{1-\frac{v^2}{c^2}}\), then what happens when the relative speed of the two inertial frames reaches or exceeds \(v=c\)? Clearly the result gives a nonsense answer, and while this is far from "proof," we will take this moment to make a declaration that we will later see to be true in many other cases...

Two inertial frames can never have a relative speed that exceeds the speed of light, and this cosmic speed limit can only be attained for light itself.

Technically, there are other phenomena besides light that can propagate at light's eponymous speed, and the criterion for this is a simple one, but we will save that discussion for later. For now, we will generalize the "cosmic speed limit" to state that no "influence" or "information" can be passed from one point in space to another at a speed faster than light can traverse the same distance.

This speed limit gives us a new perspective on time intervals between two events. We said above that there was no way to measure the proper time interval between events that are separated in space and are simultaneous, because there is no way for a single clock to get from one event to the other in time. Now we see that the two events don't need to be simultaneous for this to be true. Because of the cosmic speed limit, there is no way for the proper time interval between two events to be measured if they are separated by enough distance that light cannot travel from the earlier spacetime event to the later one.  If light can't make it in time, then neither can a clock, and the proper time cannot be measured.

Let's say that the events occur at positions \(\left(x_1,y_1,z_1\right)\) and \(\left(x_2,y_2,z_2\right)\), and times \(t_1\) and \(t_2\) (with \(t_2>t_1\)), as measured in some arbitrary inertial frame, respectively. Then there will be a well-defined proper time measurable by a moving clock if the distance between them is less than the distance that light can travel in the time interval \(\Delta t = t_2 - t_1\):

\[\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}<c\Delta t\]

We can therefore invent a sort of "discriminant" that tells us whether two events can be connected in this way:

\[\Delta s^2\equiv c^2\Delta t^2 - \left(\Delta x^2+\Delta y^2+\Delta z^2\right)\]

When \(\Delta s^2>0\), it is possible to move a clock from the earlier event to the later one, so that the clock measures the proper time, otherwise one cannot do this. This quantity \(\Delta s^2\) is called the spacetime interval between the two events.

We said that the quantities \(\Delta t\), \(\Delta x\), \(\Delta y\), and \(\Delta z\) are measured in any arbitrary inertial reference frame, but for a moment let's suppose that the events are sufficiently close together, and look at the value of the spacetime interval in the frame where the events are at the same position (i.e. the frame with the clock that, when viewed by someone else, is moved from the earlier event to the later one).  In this frame, \(\Delta x = \Delta y = \Delta z = 0\) and \(\Delta t\) is the proper time, which means:

\[\Delta s = c\Delta \tau\]

So the spacetime interval between two events is just proportional to the square of the proper time interval between those events. We stated earlier that the value of \(\Delta \tau\) is an invariant – it is the same when measured in any reference frame.  This means that all observers will agree on the spacetime interval between two events that allow for a proper time.  But now that we are talking about an abstract mathematical quantity instead of a span of time, we can make the more general statement for all pairs of events:

The spacetime interval between any two events is an invariant.

Yes, sometimes this interval is positive (allowing for a measurable proper time interval), sometimes it is negative (not allowing this - the proper time interval is imaginary, whatever that means), and sometimes it is zero (making the proper time interval zero). But whatever it comes out to, the value of \(\Delta s^2\) is measured to be the same quantity in all frames of reference.  Let's be clear about what this means: The values of \(\Delta t\), \(\Delta x\), \(\Delta y\), and \(\Delta z\) are all different for various reference frames, but the special combination of these quantities that equals \(\Delta s^2\) comes out to be the same in every frame, provided the same two events are involved.

There is one last observation we should make about the spacetime interval between two events.  Suppose we consider two events that are separated by infinitesimal differences in distance and time.  Then we have:

\[ds^2=c^2dt^2-\left(dx^2+dy^2+dz^2\right)\;\;\;\Rightarrow\;\;\;ds=dt\sqrt{c^2-\left(\left[\frac{dx}{dt}^2\right]+\left[\frac{dy}{dt}\right]^2+\left[\frac{dz}{dt}\right]^2\right)}\]

Given that the time between the infinitesimally-separated events is \(\Delta t\) and the distance in the \(x\)-direction between these events is \(\Delta x\), then the ratio \(\frac{\Delta x}{\Delta t}\) is the speed that the clock must move (measured in our arbitrary frame) in the \(x\)-direction to get from the earlier event to the later one to record both times.  The same is true for the \(y\) and \(z\) directions, so:

\[ds=dt\sqrt{c^2-\left(v_x^2+v_y^2+v_z^2\right)}=cdt\sqrt{1-\frac{v^2}{c^2}}\]

One can now imagine computing (the square root of) the spacetime interval between two events of finite separation by "chaining together" (integrating) infinitesimal intervals:

\[\Delta s=\int \limits_{event\;A}^{event\;B}ds = \int \limits_A^B cdt\sqrt{1-\frac{v^2}{c^2}}\]

Combining this with Equation 1.2.5 gives us the link between the proper time interval and the coordinate time interval between events A and B:

\[\Delta \tau = \int \limits_A^Bdt\sqrt{1-\frac{v^2}{c^2}}\]

Where \(v\) is the relative speed of the coordinate frame and the "proper frame" (the frame where the two events occur at the same place).  To avoid complications, we will assume that the path between events is a straight one, but in general it could involve constant speed or accelerated motion.  If the speed is constant, then the integral is trivial and we get the same result as Equation 1.2.2 – the inertial frame time dilation formula we found from our thought experiment.  But if the speed is not constant, then the quantity in the square root factors into the integral, and the proper time is not the same as it was for the case of the inertial frame.  Later we will see the important consequences of this.