1.3: More Thought Experiments
- Page ID
- 75011
Doppler Effect
We know that two observers in motion relative to each other measure the same speed when they look at a light wave, but what about the other properties of the light, such as the frequency and wavelength? We know that for sound they would not measure the same frequency due to the doppler effect (the phenomenon responsible for the change in perceived pitch of a car siren as it drives by), but in the case of the doppler effect for sound the medium through which the sound travels plays a critical role. In particular, an observer moving through the air toward a sound source will note that the sound wave is moving toward them faster than that sound is moving through the air. This of course is not the case for light traveling through a vacuum. Nevertheless, there is a doppler effect for light. To get started, we need to define a few things about waves:
The length of the repeating waveform, called the wavelength of the wave, we represent with the symbol \(\lambda\. A snapshot of the wave tells us something about its spatial features like the wavelength and amplitude, but the wave is moving, so if we want to know something about its time-dependence, we need to select a specific point in space, and observe the displacement of the medium (or in the case of light, where no medium is needed, the strength of something called the electromagnetic field – but more on this in classes yet to come). The wave moves at a constant speed, and the length of each repeating waveform is the same, so the time span required for a single waveform to go by is a constant for the entire wave, called the period of the wave. An alternative way of measuring the temporal feature of the wave is the rate at which the process repeats, called frequency. Frequency is measured in units of cycles per second, a unit known as hertz (Hz). Since 1 period is the time required for one cycle, there is a simple relationship between period and frequency:
\[f=\dfrac{1}{T}\]
We can make another association of periodic wave properties. If we pick a specific point on a waveform (called a point of fixed phase for the wave), and follow its motion, it should be clear that it travels a full wavelength in the time of one period. We therefore can relate the wave speed, wavelength, and period (or frequency):
\[c=\dfrac{\lambda}{T}=\lambda f\]
In the analysis to come, we will represent the "crests" of light waves with circles, so that the distance between these circles is the wavelength. We'll start with the basic phenomenon of doppler effect. The two gifs that follow apply equally to light or sound. The main idea is to note that when there is no relative motion, the rate of flashes of the red source equals the rate of flashes of the blue receiver (each flash of the receiver occurs when a crest arrives). But when the source is moving relative to the receiver, the rate of source and receiver flashes do not match. Specifically, the receiver frequency goes up when the relative motion is toward each other, and goes down when it is away from each other.
Figure 1.3.1 – No Relative Motion of Source and Receiver

Figure 1.3.2 – Approaching Relative Motion (Receiver's Perspective)

Now let's put Ann and Bob into the roles of source and receiver, respectively. We start with what Ann measures for the light source that remains stationary in her frame:
Figure 1.3.3 – Ann's Perspective of Light Signal for Two Crests
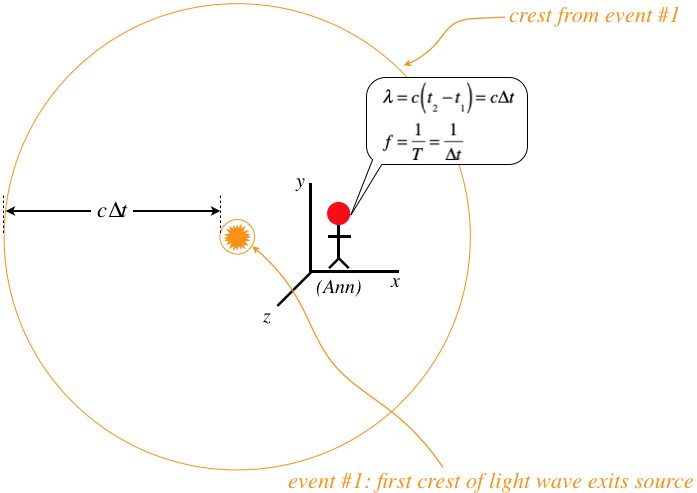
The wavelength's relationship to the frequency and wave speed is as we stated above.
Figure 1.3.4 – Bob's Perspective of Light Signal for Two Crests
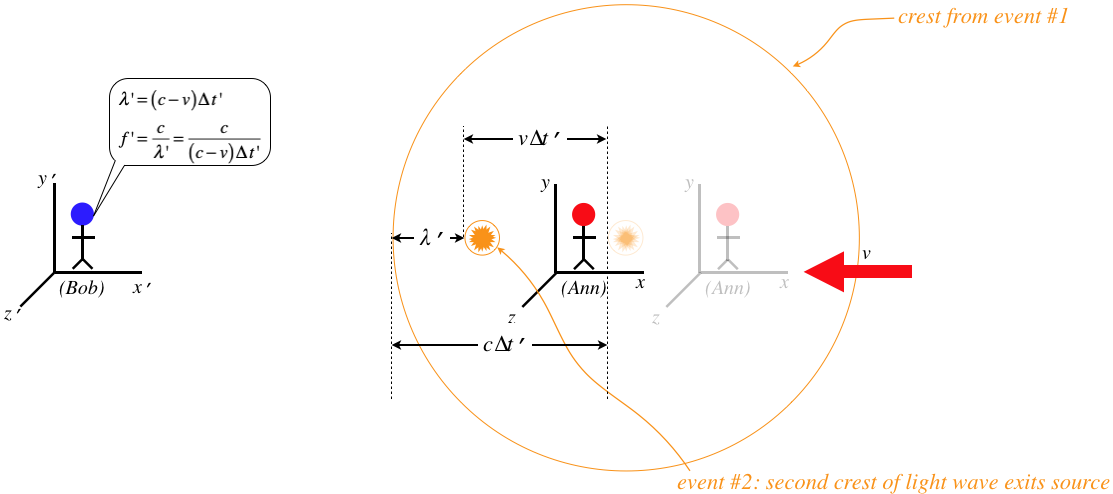
Bob's measurement of the wavelength is different from Ann's because in the time between emissions of the two wave fronts, the source moves according to Bob. But this is not the only source of the disparity between the two frequency measurements. The diagram shows that the time elapsed between wave front emissions also plays a role, and as we know, the fact that the flashes occur at the same place for Ann means that her coordinate time measurement happens to equal the proper time measurement (and she is in an interial frame, so this is also the spacetime interval), while Bob's coordinate time measurements involve events at different positions. So Bob will measure a longer time between flashes than Ann. While all waves (most notably sound) exhibit the doppler effect, the result is different for light, giving us an "ordinary" doppler effect, and a relativistic doppler effect. Plugging in the time dilation relation gives the relation between the two frequencies measured:
\[f' = \dfrac{c}{\left(c-v\right)\Delta t'}=\left(\dfrac{c}{c-v'}\right)\left(\dfrac{1}{\gamma_v\Delta t}\right)=\left(\dfrac{c}{c-v}\right)\left(\sqrt{1-\frac{v^2}{c^2}}\dfrac{1}{\Delta t}\right)=\sqrt{\dfrac{c+v}{c-v}}\;f \text{(moving toward each other)}\]
Whenever this occurs with light in the visible spectrum, the change in frequency goes away from the red end of the spectrum, and toward the blue end, so this increase in frequency for light is called a blue shift (even when the light is not in the visible spectrum).
If Ann happens to be moving away from Bob, then it is a simple change to this equation to get the correct answer – change \(v\) to \(-v\), giving:
\[f' =\sqrt{\dfrac{c-v}{c+v}}\;f \text{(moving away from each other)}\]
This effect of reducing the frequency perceived due to relative motion is called a red shift.
But of course these are not the only two options. For example, Ann and Bob may be in the process of moving past each other. If this is happening, then determining the wavelength measured by Bob is a tougher, but the time dilation between the two frames still applies. One specific example we can look at is when Bob and Ann are aligned along the \(y\)-axis. We have to be careful about using words like "when" in the context of relativity, so we will define this moment for Bob as when he sees the source of the light as being aligned with him along the \(y\)-axis (of course, he will deduce that the light source is elsewhere, but that is not what counts here, as Bob is actually observing the light). At this moment, Ann and Bob will agree upon the wavelength, since their relative motion is along the \(x\)-direction and has no effect on the spacing of wave fronts. In this case, only the time dilation plays a role, and the result is simply:
\[f' = \dfrac{1}{\Delta t'} = \dfrac{1}{\gamma_v\Delta t} = \dfrac{\sqrt{1-\frac{v^2}{c^2}}}{\Delta t}=\sqrt{1-\frac{v^2}{c^2}}\;f\]
The more general case involves the line joining the source and receiver forming an angle \(\theta\) with the relative velocity vector:
Figure 1.3.5 – Relative Motion of Source and Receiver Not Along Line Joining Them
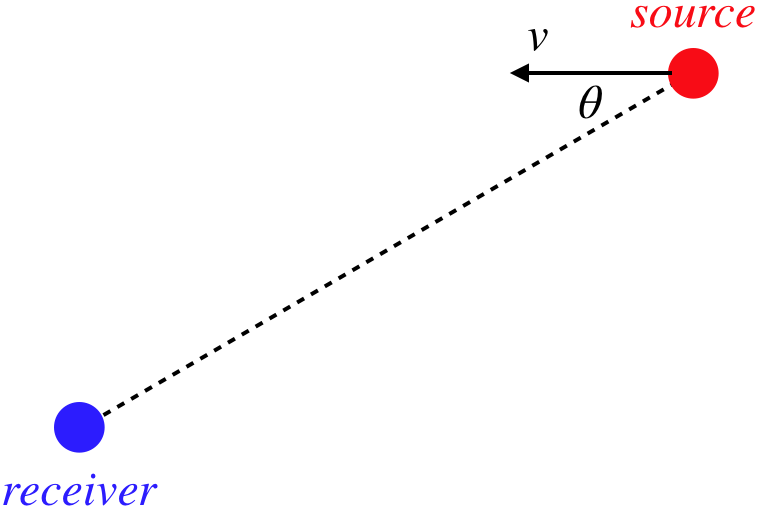
Once again, the line joins the receiver and the apparent (not deduced) source of the light. In this case, the doppler effect on the frequency comes from the component of the source's motion relative to the receiver that lies along the line joining them. That is we replace the \(v\) above with \(v\cos\theta\):
\[f' = \dfrac{c}{\left(c-v\cos\theta\right)\Delta t'} = \left(\dfrac{\sqrt{c^2-v^2}}{c-v\cos\theta}\right)f\]
It is left as an exercise for the reader to show that this equation reduces to the three equations above for the appropriate values of \(\theta\).
Simultaneity
Let's return to our discussion of how to measure coordinate time by synchronizing clocks at all the lattice points in a reference frame. Suppose Ann and Bob are moving past each other along the \(x\)-axis, and at the moment that their origins coincide, they start their clocks at the origin. Then each of them synchronizes all the clocks on their lattice with the clock at the origin. Doesn't this mean that all of Ann's clocks are synchronized with all of Bob's clocks? And if so, doesn't this mean that they should measure the same coordinate times between events, in contradiction to everything we have said fo far? Such a conundrum calls for a thought experiment!
Let's suppose Ann decides to synchronize two clocks using a flash from her clock at the origin:
Figure 1.3.6 – Simultaneous Events for Ann
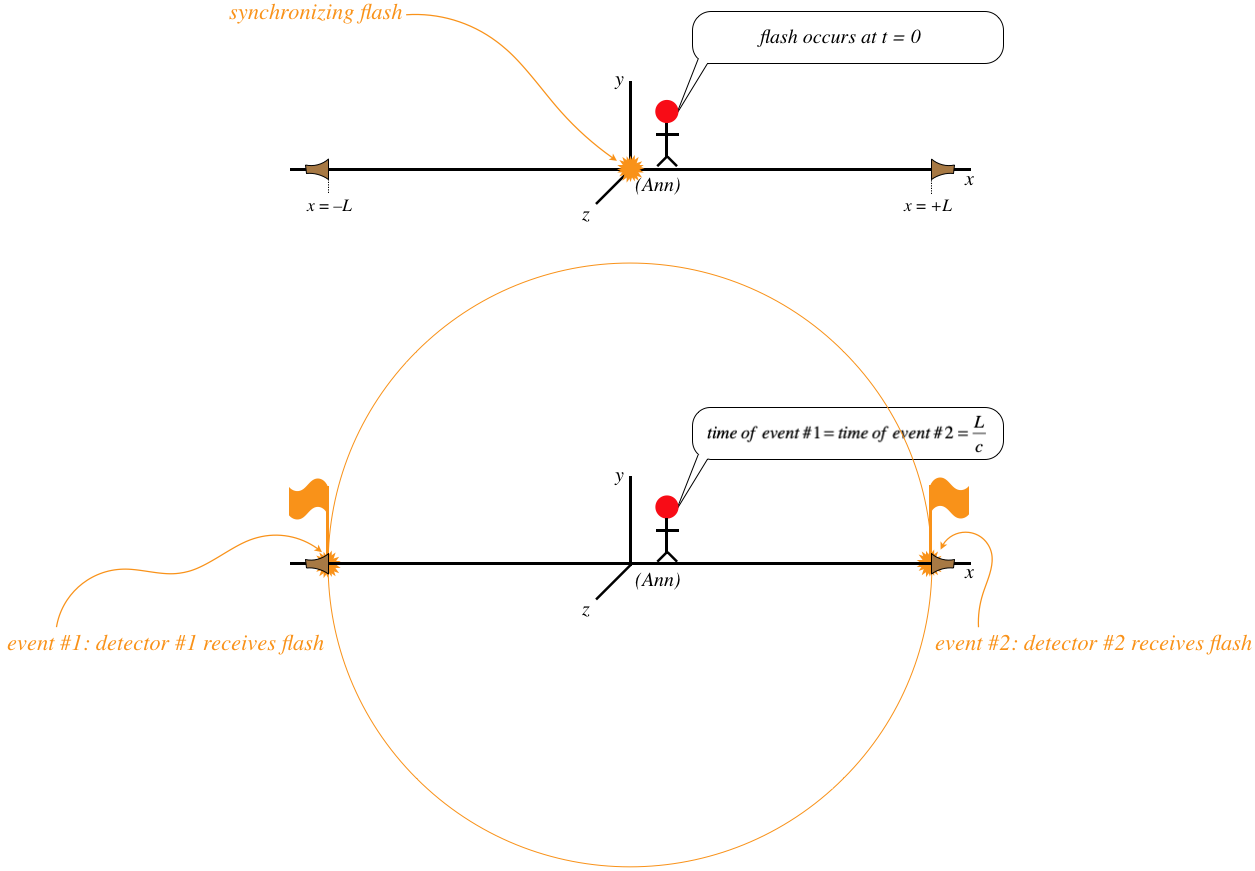
Does Bob agree that the two clocks (located at the two detectors) are synchronized? Let's look at what Bob sees:
Figure 1.3.7 – Ann's Synchronized Events Seen by Bob (a)
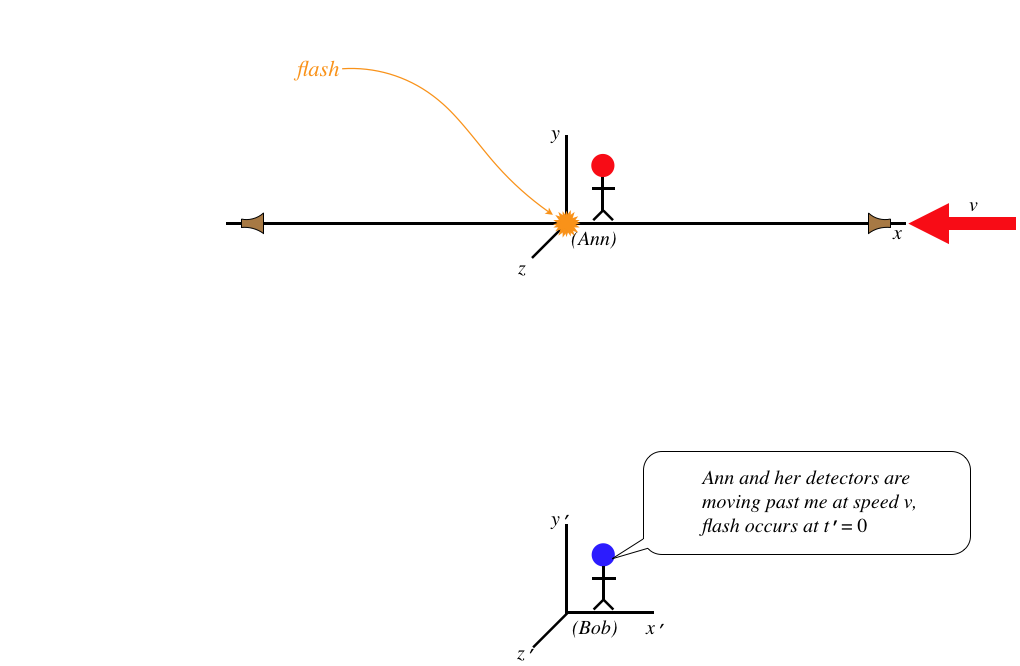
The detectors Ann is using are fixed in the lattice points in her frame, so they move along with her, according to Bob. When the light flashes, it takes time for the wave to get to the detectors, and while this time passes, the detectors move, according to Bob:
Figure 1.3.8 – Ann's Synchronized Events Seen by Bob (b)
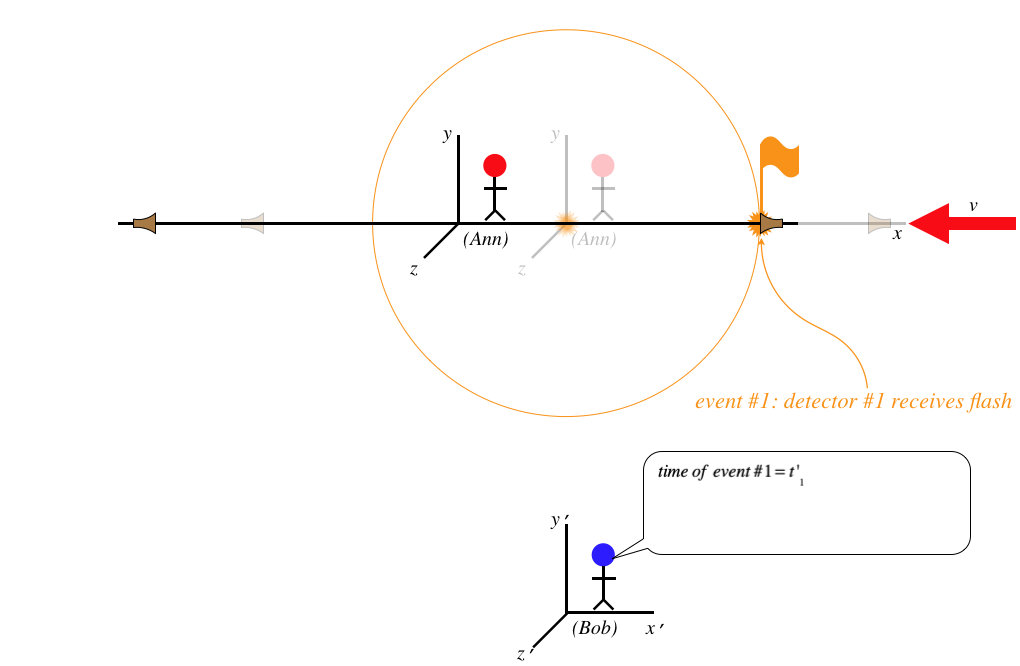
As you can see, the detector trailing Ann receives the signal before the other detector, according to Bob.
Figure 1.3.9 – Ann's Synchronized Events Seen by Bob (c)
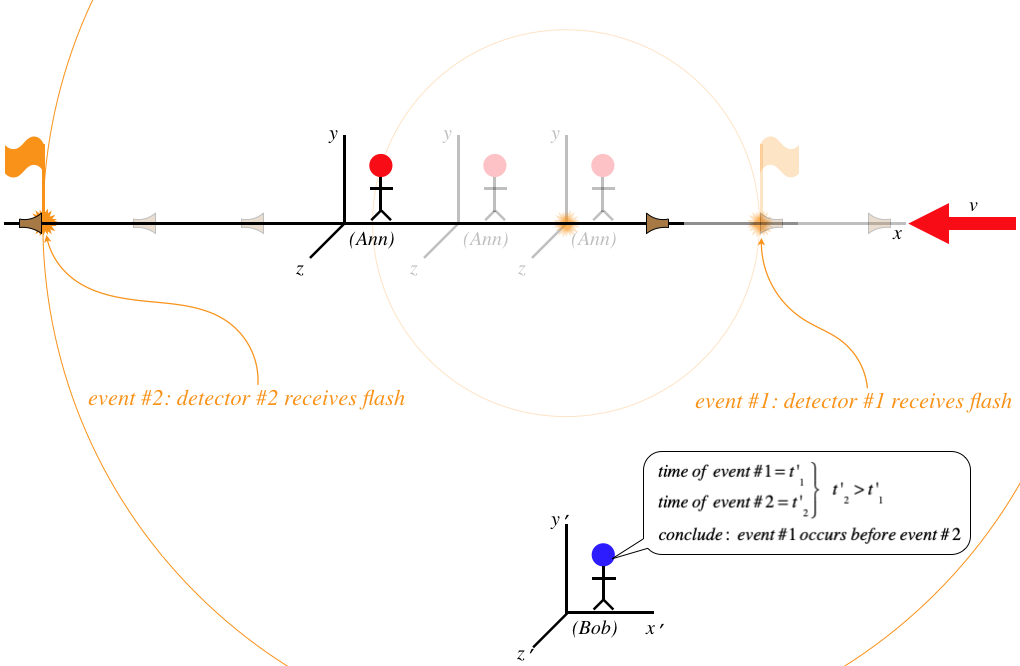
Far from seeing the two events simultaneously, Bob measures a time difference between them. This means that when he looks at all the clocks in Ann's lattice, he sees them all out of sync, with the times getting later the farther the clock is on the positive side of the origin. We therefore find that the concept of simultaneous events is relative (frame-dependent).
Alert
It is important to keep in mind that when we are talking simultaneous events in one frame, we are not talking about about simply seeing two things occur at a different time. For example, if Ann happened to be standing close to detector #1, then the light from the flag that pops up there would reach her sooner than the light coming from the flag at detector #2, and she would witness the two flags popping at different times, but the two events would still be simultaneous in her frame.
Example \(\PageIndex{1}\)
We found in the light clock thought experiment that the relationship between Ann's and Bob's time measurements is given by Equation 1.2.2. If Ann's two clocks are synchronized, then the time between the two events that occur when the flash reaches both detectors is zero. So why don't we find that for those same two events viewed by Bob, the time interval is also zero?
\[\Delta t' = \gamma_v \Delta t = 0\nonumber\]
- Solution
-
The equation quoted assumed that the time measured by Ann was the proper time, since the two events occurred at the same position in her inertial frame. The synchronized events in this case do not occur at the same position, so it is the coordinate time that she measures to be zero. One way to avoid this confusion is to write the time dilation formula of Equation 1.2.2 explicitly in terms of the proper time:
\[\Delta t' = \gamma_v \Delta \tau\nonumber\]
In the case above, the comparison is not between a coordinate time and a proper time, but two different coordinate times.
Length Contraction
Instead of comparing time spans between two frames in relative motion, let’s compare distance spans. To do this, we need to first figure out what it means to measure the length of an object (say a meter stick). As we know, whatever we do in relativity must be in terms of spacetime events. We can’t simply say that the length of an object is the distance between events that occur at the object’s endpoints, because the object might move after one event occurs and before the second one occurs. So clearly to define the length of an object, we need to stipulate that the two events that occur at the endpoints of the object being measured occur at the same time. But since observers in two frames in relative motion will not agree to what events are simultaneous, it stands to reason that they might not agree to length measurements.
We consider The following scenario: Ann lays a rod down along her \(x\)-axis, and as she passes by Bob, each end of the rod creates a spark (constituting a spacetime event) when it coincides with a device stationary in Bob's frame that we will call a "sparker."
Figure 1.3.10 – Ann Measures the Length of the Rod
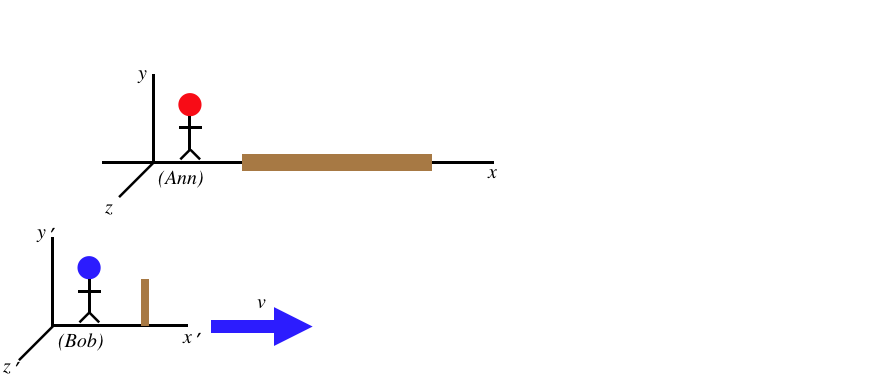
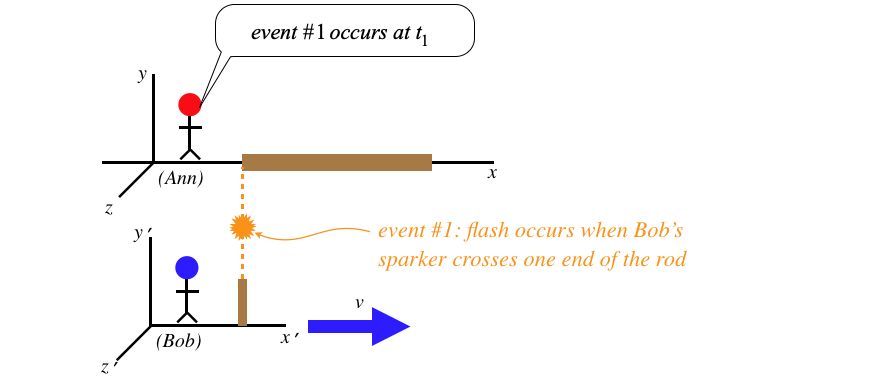
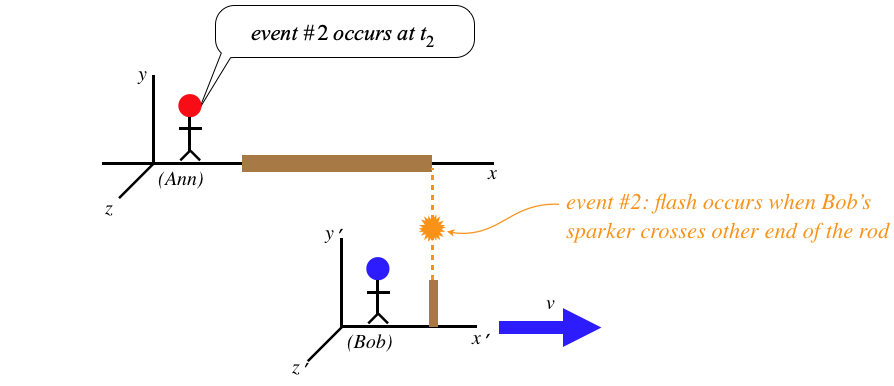
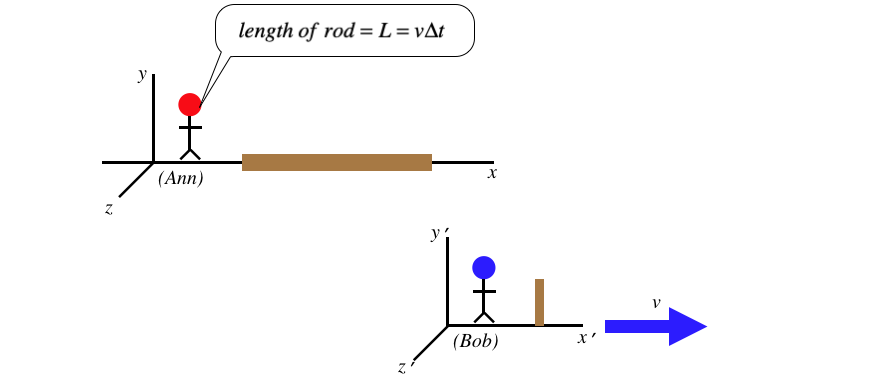
Ann measures the length of her rod to be the speed of Bob's sparker multiplied by the coordinate time she measures between the two events. The way Bob measures the length of the rod is similar:
Figure 1.3.11 – Bob Measures the Length of the Rod
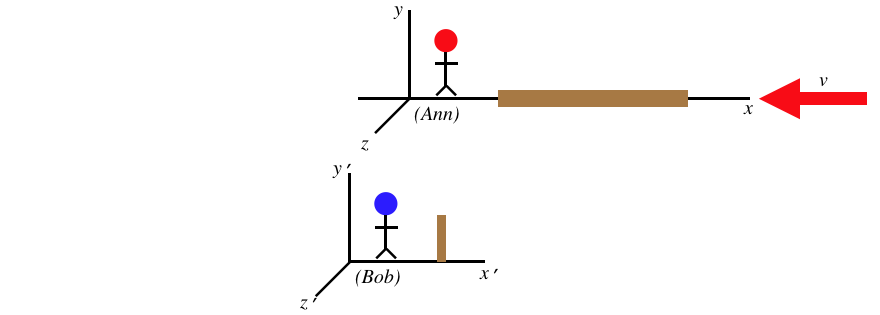
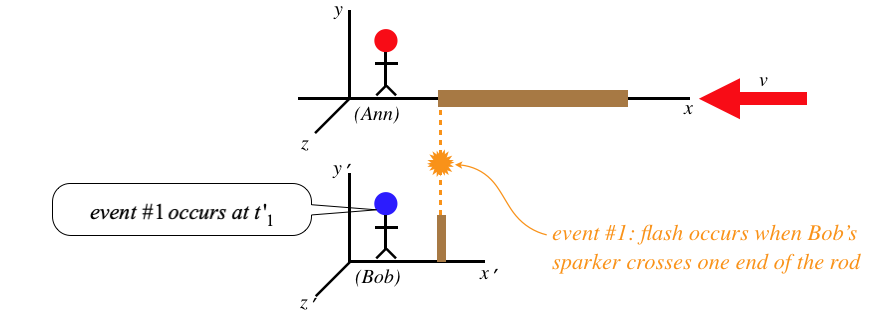
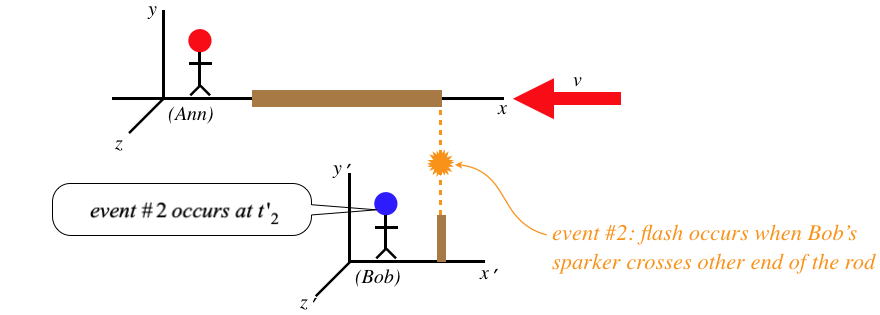
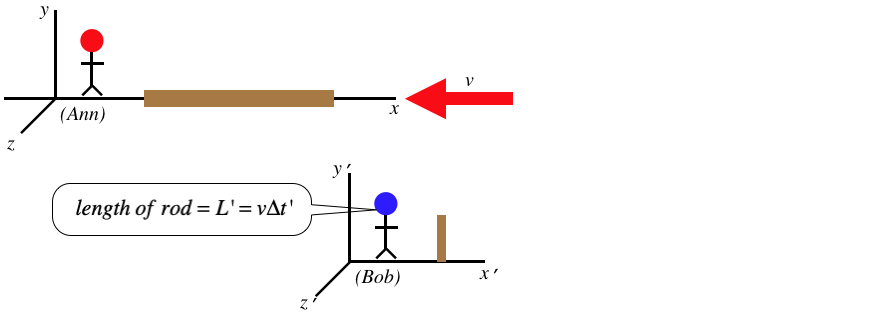
We can now use the time dilation formula that relates these two times to determine a relationship between the two measured lengths, but we have to be very careful here. Namely, we must ask ourselves, whose measures the dilated time here? Put another way, which of these two observers measures the proper time between the two events? The answer is clearly Bob, since both events occur at the end of his sparker, which is at rest in his frame, meaning that both events occur at the same place – the exact criterion for proper time. Therefore we find that it is Ann's time between events that is longer than the time measured by Bob, giving:
\[\Delta t = \gamma_v \Delta t' \;\;\;\Rightarrow\;\;\; L' = v\Delta t' = v\dfrac{\Delta t}{\gamma_v} = \dfrac{L}{\gamma_v}\]
So Bob measures the rod to be shorter than Ann measures it to be (recall \(\gamma_v>1\)). This phenomenon is known as length contraction.
A few comments about this result:
- The longest possible measurement of length occurs in the rest frame of the object whose length is being measured. This length is often referred to as the proper length.
- We are accustomed to attributing different visual observations of the same object to optical illusions. This is not one of those cases. The same rod is shorter for Bob than it is for Ann. Length is not an intrinsic property – it is observer-dependent.
- If Bob zooms by Ann with an identical rod, then Bob will measure Ann’s rod to be shorter than his own, and Ann will measure Bob’s rod to be shorter than hers. We will explore this seeming paradox soon, but the short answer is that length is not a quality that is inherent to an object, so the fact that the rods are identical does not mean that their lengths are. Most people are not bothered by the fact that two identical rods may have different colors (due to red/blue shift), because it isn’t too difficult to accept that color is not a property inherent to objects, but length is significantly tougher to swallow. If it helps, it’s okay to say that identical objects have equal proper lengths.
- If we consider examining the same rod in both frames when it is aligned along the \(y\)-axis (while relative motion is still along the \(x\)-axis), we will fairly easily find that both observers agree on the length. Put another way, lengths contract only along the dimension parallel to the direction of relative motion.
- In terms of the lattice points for the two frames, we would say that Bob sees Ann's lattice points ate closer together along the \(x\)-direction that his own, and Ann would conclude the same about Bob's lattice points. This is because each can measure the rod in terms of these points, so if the length of the rod is relative, so is the entire space of the moving item.
Angles
Consider our usual setup with Ann and Bob in relative motion along their common \(x\)-axis. We know that there is a contraction of length along the \(x\)-axis when an object is moving relative to the frame it is viewed in. Furthermore, we know that lengths along the \(y\) and \(z\) axes do not contract. Suppose Ann has a right-triangular wooden block at rest in her frame as in the figure below, and measures the angle it makes with the \(x\)-axis to be \(\theta\). What angle does Bob measure?
Figure 1.3.12 – Ann and Bob Measure an Angle
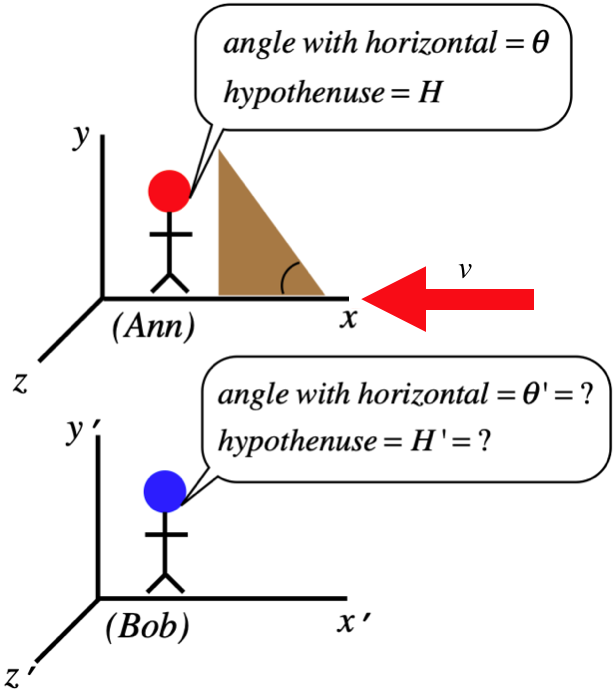
With only the side of the triangle along the \(x\)-axis contracting, the angle must change. If we call the length of the base of the triangle in Ann's frame \(x\) and the height \(y\), then we get:
\[\theta ' = \tan^{-1}\left(\dfrac{y'}{x'}\right) = \tan^{-1}\left(\dfrac{y}{\frac{x}{\gamma_v}}\right) = \tan^{-1}\left(\gamma_v\dfrac{y}{x}\right) = \tan^{-1}\left(\gamma_v \tan\theta\right)\]
Example \(\PageIndex{1}\)
Compute Bob's unanswered question in the figure above – what does he measure for the hypotenuse of the triangle, in terms of the hypotenuse and angle measured by Ann?
- Solution
-
Start with the Pythagorean theorem:
\[H' = \sqrt{x'^2+y'^2} = \sqrt{\dfrac{x^2}{\gamma_v^2}+y^2} = \sqrt{\left(1-\frac{v^2}{c^2}\right)x^2+y^2} = \sqrt{x^2+y^2-\frac{v^2}{c^2}x^2}\nonumber\]
Now write Ann's values of \(x\) and \(y\) in terms of \(H\) and \(\theta\):
\[\left. \begin{array}{l} H^2=x^2+y^2 \\ x = H\cos\theta \end{array} \right\}\;\;\; H' = \sqrt{H^2-\frac{v^2}{c^2}H^2\cos^2\theta} = H\sqrt{1-\frac{v^2}{c^2}\cos^2\theta}\nonumber\]


