2.4: Momentum Conservation
- Page ID
- 21813
Another Thought Experiment
We have completed our exploration of the fundamentals of relativistic kinematics and its consequences. Now it is time to examine the consequences of the relativity principle in the area of dynamics. Our first clue that something needs to be done differently comes from the basis of all dynamics: Newton's laws of motion. In particular, the second law looks like:
\[\overrightarrow F_{net} = \dfrac{d\overrightarrow p_{cm}}{dt}\]
The obvious question is, with respect to what time measurement is this momentum changing? This is actually a very difficult problem to deal with in relativity in that it is difficult to apply the relativity principle, so we will instead look at a consequence of this law – momentum conservation. If someone in one frame observes a collision of two objects and declares that momentum is conserved, then an observer in another frame watching the same collision should conclude the same thing. Momentum conservation is among the most cherished principles of physics, and if an experiment could be performed where two inertial observers do not agree that it is upheld, then that would cause problems for the relativity principle. This calls for a thought experiment!
We have three players involved here (Ann, Bob, and Chu), and we are initially viewing the activities from Chu's perspective, who sees Ann moving in the \(-x\)-direction and Bob moving in the \(+x\)-direction at equal speeds. Ann and Bob both throw identical balls in a direction that is (from their own perspectives) along their \(y\) axes, at speeds they each measure to be \(u\). The balls collide elastically with each other, and return to where they started.
Figure 2.4.1 – Chu Observes Collision
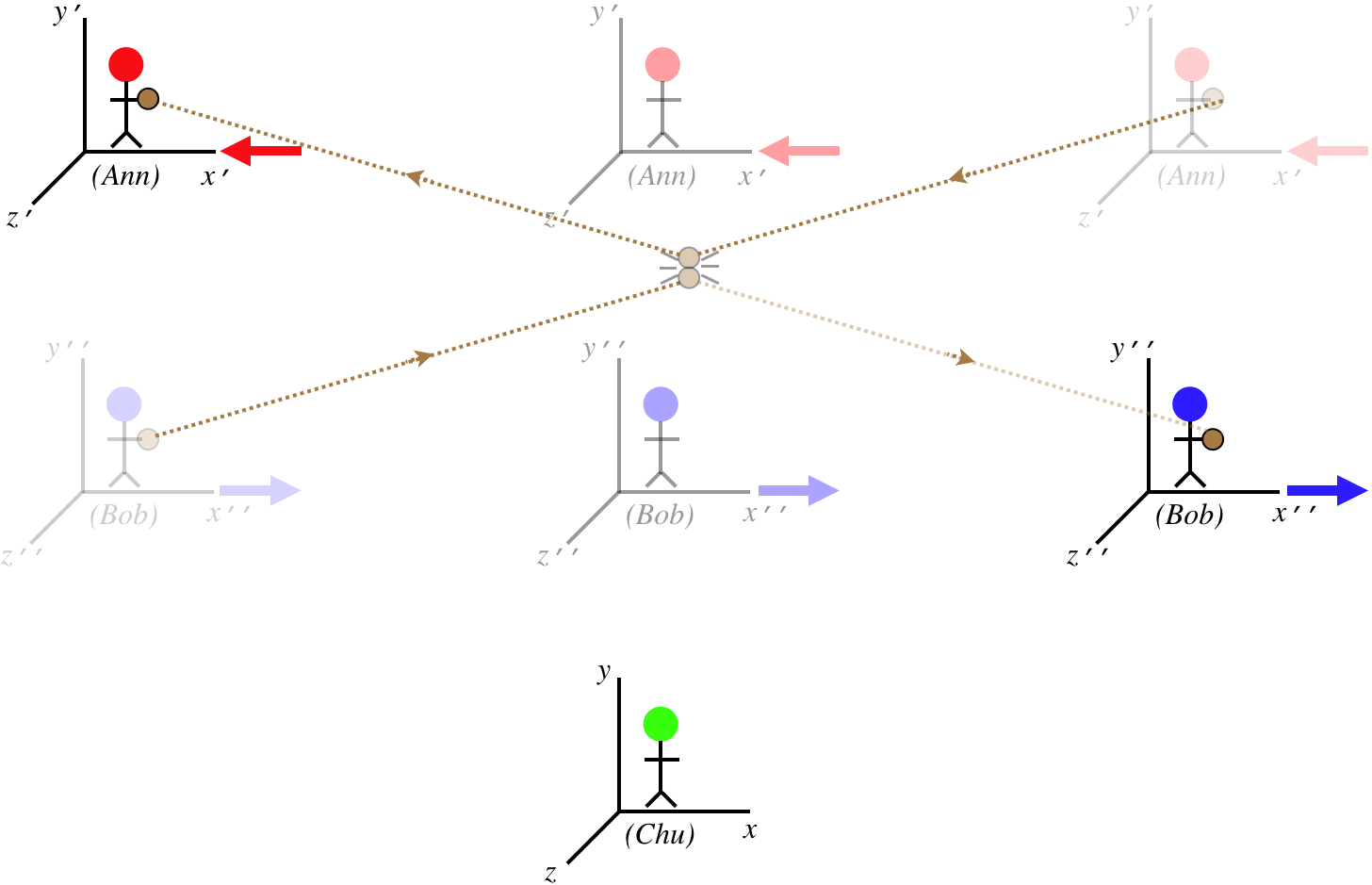
From Chu's perspective, everything is completely symmetric, and so he concludes that the momentum (and most notably, the \(y\)-component of the momentum) in this collision is conserved. Okay, let's confirm that all observers agree upon this basic physics principle by looking at the very same collision from Bob's perspective. To Bob, his ball's motion parallels his \(y\)-axis, while Ann's has an \(x\)-component (equal to her frame's relative motion).
Figure 2.4.2 – Bob Observes Collision
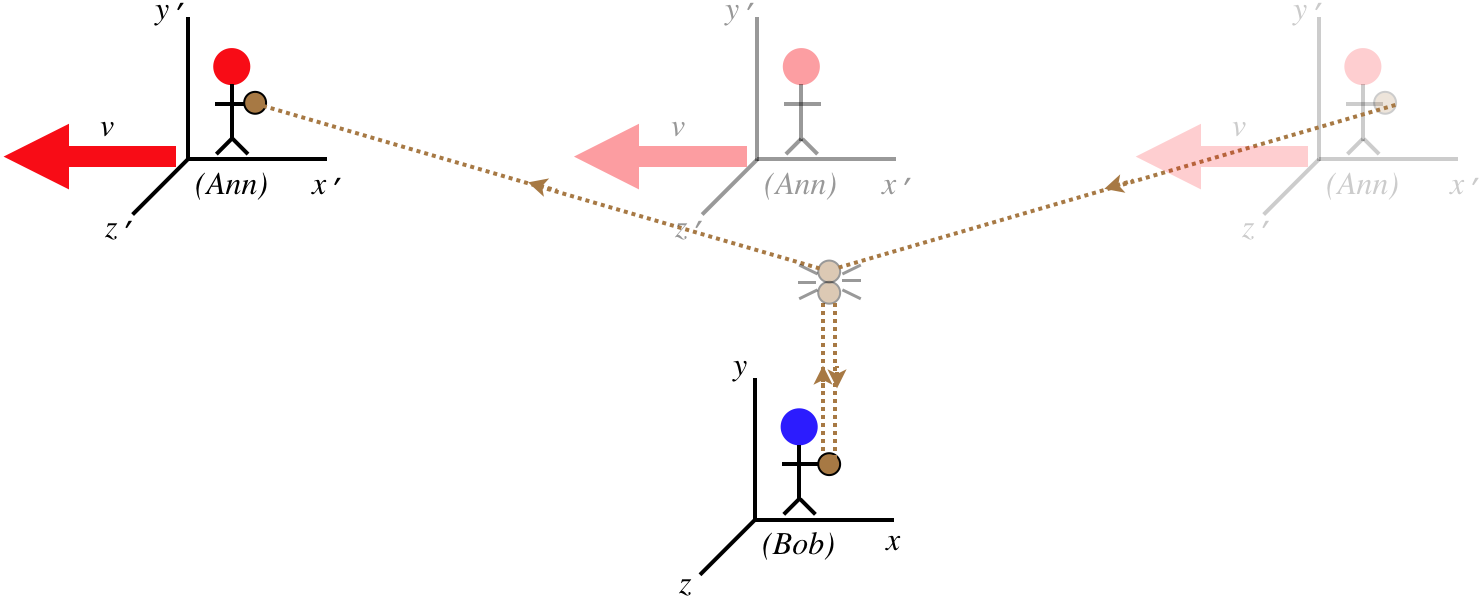
Bob now compares the \(y\)-components of velocity of the two balls. We already stated that Bob measures the velocity of his ball to be \(u\), and Ann measures velocity of her ball to be the same, but because of the strangeness of velocity, neither agrees that the other ball is moving that fast. Bob says that the \(y\)-component of velocity of Ann's ball is (\(u_x\) and \(u_y\) are the \(x\) and \(y\) components of Ann's ball, respectively, according to Ann):
\[u'_y\left(\text{Ann's ball}\right) = \dfrac{u_y}{\gamma_v\left(1-\frac{u_xv}{c^2}\right)} = \dfrac{u}{\gamma_v\left(1-0\right)}=\dfrac{u}{\gamma_v}\]
This is smaller than the vertical speed that Bob measures for his own ball, which means that Ann's ball (which has the same mass as his ball) had to have less momentum going into the collision than his ball. But he sees is own ball come back at the same speed that it left, and the collision is elastic (his ball isn't any warmer), and these are properties of a head-on collision with an identical ball moving at the same speed in the opposite direction if momentum is conserved. So something is wrong here.
A New-and-Improved Momentum
There are only three possible conclusions we can draw from the discrepancy shown in this thought experiment:
- Momentum conservation is not a fundamental principal of physics, since one observer measuring no change in momentum (in the example above, Chu) for a closed system does not ensure that every other observer (Ann and Bob) gets that same result.
- Mass is measured differently in different reference frames. If Bob measures the mass of Ann's ball to be greater than his own, then that could compensate for the lower velocity so that their two balls once again have equal \(y\)-components of momenta.
- Our definition of momentum, while useful for low velocities, needs a facelift to handle relativistic speeds.
For physicists, stopping at the first of these was never an option – conservation principles and momentum in particular had been revered for far too long. In the early years (and for quite some time afterward), the second option was the accepted explanation, and it works fine. In modern times, however, the physics community has instead embraced the third option – we prefer to characterize mass as an invariant quantity that is inherent to matter, and simply admit that our original definition of momentum was insufficient.
Deriving the correct form of the momentum is challenging until we get to 4-vectors in a future chapter, so right now we will just be given this formula and confirm that it works for the Ann/Bob/Chu thought experiment above. For an object moving at a speed \(u\) relative to an observer, the momentum of the object in the frame of that observer is defined to be:
\[\overrightarrow p \equiv m \gamma_u \overrightarrow u\]
Alert
Up to now, we have usually dealt with \(\gamma_v\) that relates the frames of two observers, whose relative speed we define as '\(v\),' but here the \(\gamma_u\) relates the frame of the observer to that of the moving object, not another observer. As we will be relating the momenta in frames of observers, it will be important to keep straight the difference between \(\gamma_v\) and \(\gamma_u\). As one example, if we have two observers, the \(\gamma_v\) that relates their frames are the same for both of them, but the \(\gamma_u\) that one observer uses for a moving object is not the same as the \(\gamma_u'\) used by the other observer for the same moving object, since \(u \ne u'\).
As a first check, it is clear that at slow velocities, momentum reduces to our usual definition of momentum, since for \(u<<c\), \(\gamma_u\rightarrow 1\).
Proving that this form of momentum is conserved in the thought experiment above requires careful accounting of velocities, as there are many involved here. In an effort to not have to carry primes on all our variables through the calculation, we will look at this collision from Ann's perspective – clearly the collision has all the same features for her that it has for Bob. We will use the subscript 'A' whenever referring to a quantity specifically related to Ann's ball, and use a 'B' for Bob's ball. We seek to write all of these quantities in terms of the value \(u\), the speed that each measures for their own ball; and \(v\), the relative speed of their two frames.
We need the \(\gamma\)'s for the two balls from Ann's perspective in order to compare momenta in her frame. The \(\gamma\) for her ball is easy, as she sees it moving with a speed of \(u\):
When Ann looks at the ball thrown by Bob, she sees that it has an \(x\)-component equal to \(+v\), and its \(y\)-component is determined from the velocity addition formula. Bob sees no \(x'\) component for his ball's velocity \(u'_{Bx}=0\), and he measures the \(y'\) component for his ball's velocity to be \(u'_{By}=u\), so using the velocity addition formula to determine the two components of velocity of Bob's ball in Ann's frame gives:
\[\begin{array}{l} u_{Bx} = \dfrac{u'_{Bx}+v}{1+\frac{u'_{Bx}v}{c^2}} = \dfrac{0+v}{1+0} = v \\ u_{By} = \dfrac{u'_{By}}{\gamma_v\left(1+\frac{u'_{Bx}v}{c^2}\right)} = \dfrac{u}{\gamma_v\left(1+0\right)} = \dfrac{u}{\gamma_v} \end{array}\]
We now need to construct the \(\gamma_u\) for Bob's ball as seen by Ann, which means we first need to construct the square of the speed for Bob's ball according to Ann:
\[u_B^2 = u_{Bx}^2 +u_{By}^2 = v^2 + \dfrac{u^2}{\gamma_v^2} \;\;\;\Rightarrow \;\;\; \gamma_{uB} = \dfrac{1}{\sqrt{1-\frac{u_B^2}{c^2}}} = \dfrac{1}{\sqrt{1-\frac{v^2}{c^2}-\frac{u^2}{\gamma_v^2 c^2}}} \]
Plugging this in gives the \(y\)-component of momentum of Bob's ball as measured by Ann, which we can then compare to the momentum of Ann's ball (which is entirely in the \(y\)-direction):
\[p_{By} = \gamma_{uB}\;m\;u_{By} = \dfrac{1}{\sqrt{1-\frac{v^2}{c^2}-\frac{u^2}{\gamma_v^2 c^2}}}\;m \;\dfrac{u}{\gamma_v}\]
Showing that momentum is conserved with its new definition is now a matter of showing that this equals the magnitude of Equation 2.4.4:
\[\dfrac{1}{\sqrt{1-\frac{v^2}{c^2}-\frac{u^2}{\gamma_v^2 c^2}}}\;\cancel{m} \;\dfrac{\cancel{u}}{\gamma_v} = \dfrac{\cancel{m\;u}}{\sqrt{1-\frac{u^2}{c^2}}}\]
Inverting and squaring both sides of the equation and simplifying completes the proof:
\[\left(1-\frac{v^2}{c^2}-\frac{u^2}{\gamma_v^2 c^2}\right)\gamma_v^2 = 1-\frac{u^2}{c^2} \;\;\; \Rightarrow \;\;\; \cancelto{1}{\left(1-\frac{v^2}{c^2}\right) \gamma_v^2} - \frac{u^2}{c^2} = 1-\frac{u^2}{c^2}\]
Due to the symmetry of the two cases, it should be clear that Bob will get the same result, and from Chu's perspective, the new version of momentum changes the magnitude of the momenta of both balls equally, so he will naturally again witness momentum conservation. Indeed, with this new definition of momentum, every frame will agree that it is conserved before and after the collision.


