3.7: Rotation of Axes, Three Dimensions. Eulerian Angles
- Page ID
- 8114
We now consider two sets of orthogonal axes \(\text{O}x, \ \text{O}y, \ \text{O}z\) and \(\text{O}x^\prime, \ \text{O}y^\prime, \ \text{O}z^\prime\) in three-dimensional space and inclined to each other. A point in space can be described by its coordinates \((x,y,z)\) with respect to one basis set or \((x^\prime ,y^\prime ,z^\prime)\) with respect to the other. What is the relation between the coordinates \((x,y,z)\) and the coordinates \((x^\prime ,y^\prime ,z^\prime)\)?
We first need to describe exactly how the primed axes are inclined with respect to the unprimed axes. In the figure below are shown the axes \(\text{O}x, \ \text{O}y\) and \(\text{O}z\). Also shown are the axes \(\text{O}x^\prime\) and \(\text{O}z^\prime\); the axis \(\text{O}y^\prime\) is directed behind the plane of the paper and is not drawn. The orientation of the primed axes with respect to the unprimed axes is described by three angles \(θ , \ \phi\) and \(ψ\), known as the Eulerian angles, and they are shown in figure \(\text{III.19}\).
The precise definitions of the three angles can be understood by three consecutive rotations, illustrated in figures \(\text{III.20,21,22}\).
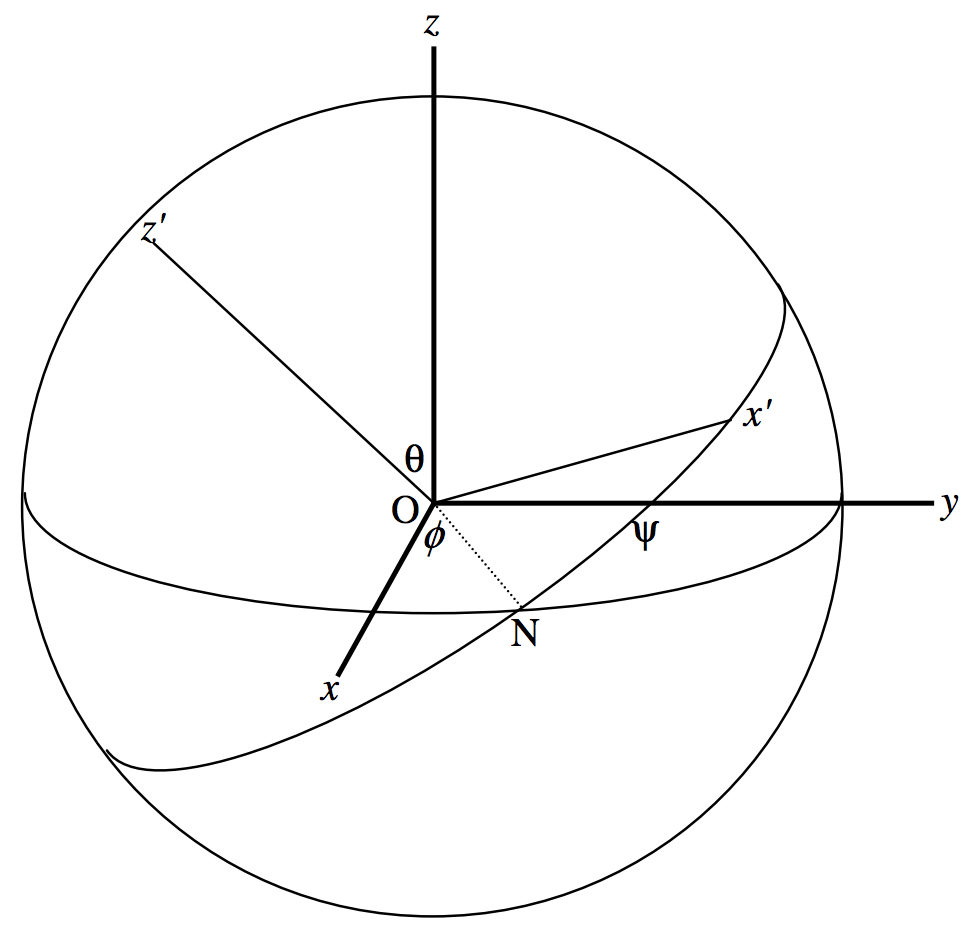
\(\text{FIGURE III.19}\)
First, a rotation through \(\phi\) counterclockwise around the \(\text{O}z\) axis to form a set of intermediate axes \(\text{O}x_1 , \ \text{O}y_1 , \ \text{O}z_1\), as shown in figure \(\text{III.20}\). The \(\text{O}z\) and \(\text{O}z_1\) axes are identical. Part (b) shows the rotation as seen when looking directly down the \(\text{O}z\) (or \(\text{O}z_1\) ) axis.
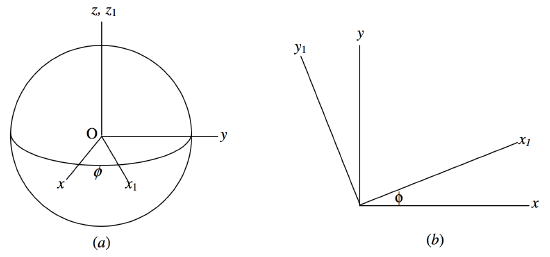
\(\text{FIGURE III.20}\)
The relation between the \((x, y, z)\) and \((x_1, \ y_1 , \ z_1)\) coordinates is
\[\pmatrix{x_1 \\ y_1} = \pmatrix{\cos \phi & \sin \phi \\ -\sin \phi & \cos \phi} \pmatrix{x \\ y}. \label{3.7.1} \tag{3.7.1}\]
Next, a rotation through \(θ\) counterclockwise around the \(\text{O}x_1\) axis to form a set of axes \(\text{O}x_2 , \ \text{O}y_2 , \ \text{O}z_2\). The \(\text{O}x_1\) and \(\text{O}x_2\) axes are identical (Figure \(\text{III.21}\)). Part (b) of the figure shows the rotation as seen when looking directly towards the origin along the \(\text{O}x_1\) (or \(\text{O}x_2\) ) axis.
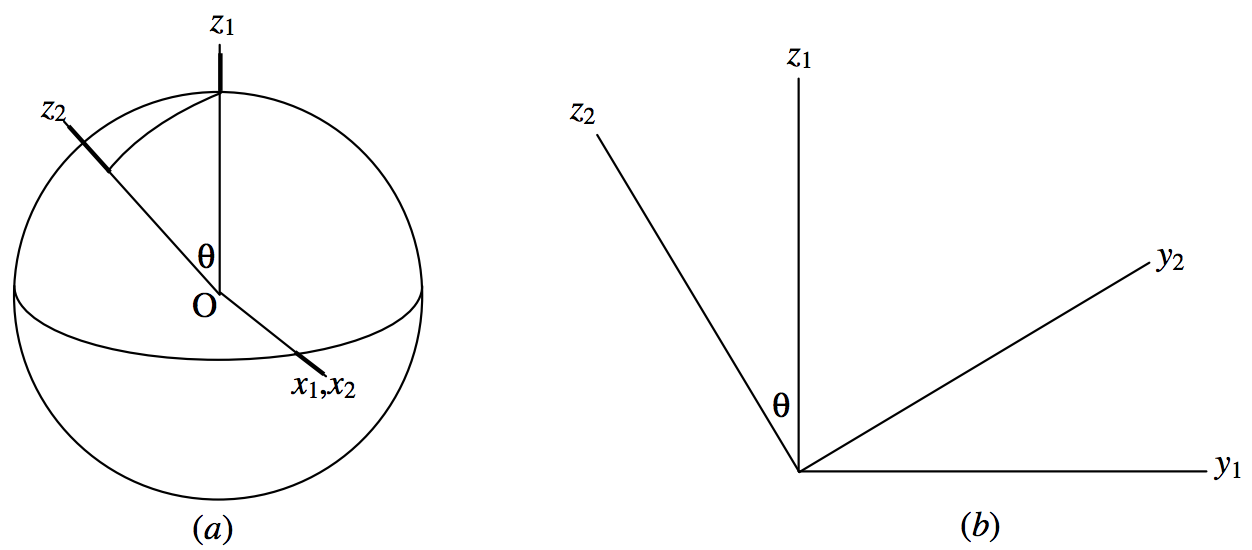
\(\text{FIGURE III.21}\)
The relation between the \((x_1 , y_1 , z_1)\) and \((x_2 , y_2 , z_2)\) coordinates is
\[\pmatrix{y_2 \\ z_2} = \pmatrix{\cos θ & \sin θ \\ -\sin θ & \cos θ} \pmatrix{y_1 \\ z_1}. \label{3.7.2} \tag{3.7.2}\]
Lastly, a rotation through \(ψ\) counterclockwise around the \(\text{O}z_2\) axis to form the set of axes \(\text{O}x^\prime, \text{O}y^\prime , \text{O}z^\prime\) (figure \(\text{III.22}\)). The \(\text{O}z_2\) and \(\text{O}z^\prime\) axes are identical. Part (b) of the figure shows the rotation as seen when looking directly down the \(\text{O}z_2\) (or \(\text{O}z^\prime\)) axis.
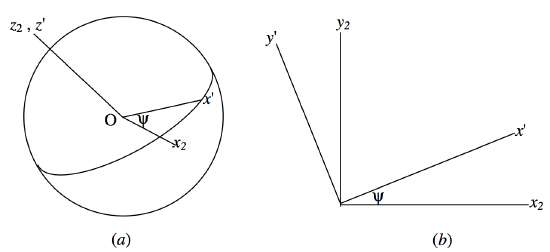
\(\text{FIGURE III.22}\)
The relation between the \((x_2 , y_2 , z_2)\) and \((x^\prime , y^\prime , z^\prime)\) coordinates is
\[\pmatrix{x^\prime & y^\prime & z^\prime} = \pmatrix{\cos ψ & \sin ψ & 1 \\ -\sin ψ & \cos ψ & 0 \\ 0 & 0 & 0} \pmatrix{x_2 \\ y_2 \\ z_2}. \label{3.7.3} \tag{3.7.3}\]
Thus we have for the relations between \((x^\prime ,y^\prime ,z^\prime)\) and \((x,y,z)\)
\[\pmatrix{x^\prime \\ y^\prime \\ z^\prime} = \pmatrix{\cos ψ & \sin ψ & 0 \\ -\sin ψ & \cos ψ & 0 \\ 0 & 0 & 1} \pmatrix{1 & 0 & 0 \\ 0 & \cos θ & \sin θ \\ 0 & -\sin θ & \cos θ} \pmatrix{\cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1} \pmatrix{x \\ y \\ z}. \label{3.7.4} \tag{3.7.4}\]
On multiplication of these matrices, we obtain
\[\pmatrix{x^\prime \\ y^\prime \\ z^\prime} = \pmatrix{ \cos ψ \cos \phi - \cos θ \sin \phi \sin ψ & \cos ψ \sin \phi + \cos θ \cos \phi \sin ψ & \sin ψ \sin θ \\ -\sin ψ \cos \phi - \cos θ \sin \phi \cos ψ & -\sin ψ \sin \phi + \cos θ \cos \phi \cos ψ & \cos ψ \sin θ \\ \sin θ \sin \phi & - \sin θ \cos \phi & \cos θ} \pmatrix{x \\ y \\ z}. \label{3.7.5} \tag{3.7.5}\]
The inverse of this may be found, as in the two-dimensional case, either by solving these three Equations for \(x\), \(y\) and \(z\) (which would be rather tedious); or by interchanging the primed and unprimed quantities and reversing the order and signs of all operations (replace \(ψ\) with \(−\phi\), \(θ\) with \(−θ\), and \(\phi\) with \(−ψ\)) which is less tedious; or by recognizing that the determinant of the matrix is unity and therefore its reciprocal is its transpose, which is hardly tedious at all. The reader should verify that the determinant of the matrix is unity by multiplying it out and making use of trigonometric identities. The reason that the determinant must be unity, however, and that the rotation matrix must be orthogonal, is that rotation of axes cannot change the magnitude of a vector.
Each element of the matrix is the cosine of the angle between an axis in one basis set and an axis in the other basis set. For example, the second element in the first row is the cosine of the angles between \(\text{O}x^\prime\) and \(\text{O}y\). The first element of the third row is the cosine of the angles between \(\text{O}z^\prime\) and \(\text{O}x\). The matrix can be referred to as the matrix of direction cosines between the axes of one basis set and the axes of the other basis set, and the relations between the coordinates can be written
\[\pmatrix{x^\prime \\ y^\prime \\ z^\prime} = \pmatrix{c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33}} \pmatrix{x \\ y \\ z} \label{3.7.6} \tag{3.7.6}\]
\[\textbf{R}^\prime = \textbf{CR}. \label{3.7.7} \tag{3.7.7}\]
You will note the similarity of the forms of the direction cosines to the cosine formula for the solution of a spherical triangle, and indeed the direction cosines can all be derived by drawing and solving the relevant spherical triangles. You might (or might not!)enjoy trying to do this.
The matrix \(\textbf{C}\) of the direction cosines is orthogonal, and the properties of an orthogonal matrix are as follows. The reader should verify this using the formulas for the direction cosines in terms of the Eulerian angles. The properties also apply, of course, although more trivially, to the rotation matrix in two dimensions.
- det \(\textbf{C} = \pm 1\) and (det \(\textbf{C} = -1\) implies that the two basis sets are of opposite chirality or "handedness"; that is, if one basis set is right-handed, the other is left-handed.)
- The sum of the squares of the elements in any row or any column is unity. This merely means that the magnitudes of unit orthogonal vectors are indeed unity.
- The sum of the products of corresponding elements in any two rows or any two columns is zero. This is merely a reflection of the fact that the scalar o dot product of any two unit orthogonal vectors is zero.
- Every element is equal to its own cofactor. This a reflection of the fact that the vector or cross product of any two unit orthogonal vectors in cyclic order is equal to the third.
- \(\textbf{C}^{-1} = \tilde{\textbf{C}}\), or the reciprocal of an orthogonal matrix is equal to its transpose.
The first four properties above can be (and should be) used in a numerical case to verify that the matrix is indeed orthogonal, and they can be used for detecting and for correcting mistakes.
For example, the following matrix is supposed to be orthogonal, but there are, in fact, two mistakes in it. Using properties (b) and (c) above, locate and correct the mistakes. (It will become clear when you do this why verification of property (b) alone is not sufficient.) When you have corrected the matrix, see if you can find the Eulerian angles \(θ\), \(\phi\) and \(ψ\) without ambiguity of quadrant. As a hint, start at the bottom right hand side of the matrix and note, from the way in which the Eulerian angles are set up, that \(θ\) must be between \(0^\circ\) and \(180^\circ\), so that there is no ambiguity of quadrant. The other two angles, however, can lie between \(0^\circ\) and \(360^\circ\) and must be determined by examining the signs of their sines and cosines. When you have calculated the Eulerian angles, a further useful exercise would be to prepare a drawing showing the orientation of the primed axes with respect to the unprimed axes.
\[\pmatrix{+ 0.075 \ 284 \ 882 \ 7 & -0.518 \ 674 \ 468 \ 2 & +0.851 \ 650 \ 739 \ 6 \\ -0.553 \ 110 \ 473 \ 2 & -0.732 \ 363 \ 000 \ 8 & +0.397 \ 131 \ 261 \ 9 \\ -0.829 \ 699 \ 337 \ 5 & + 0.442 \ 158 \ 963 \ 2 & -0.342 \ 020 \ 143 \ 3}\]
Note, as a matter of good computational practice, that the numbers are written in groups of three separated by half spaces after the decimal point, all numbers, positive and negative, are signed, and leading zeroes are not omitted.


