15.5: Maxwell's Third Equation
- Page ID
- 5340
This is derived from Ampère's theorem, which is that the line integral of the magnetic field \(\textbf{H}\) around a closed circuit is equal to the enclosed current.
Now there are two possible components to the "enclosed" current, one of which is obvious, and the other, I suppose, could also be said to be "obvious" once it has been pointed out! Let's deal with the immediately obvious one first, and look at Figure XV.1.
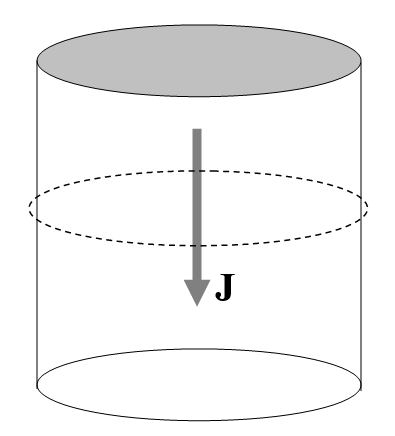
FIGURE XV.1
In Figure XV.1, I am imagining a metal cylinder with current flowing from top to bottom - i.e. electrons flowing from bottom to top. It needn't be a metal cylinder, though. It could just be a volume of space with a stream of protons moving from top to bottom. In any case, the current density (which may vary with distance from the axis of the cylinder) is \(\textbf{J}\), and the total current enclosed by the dashed circle is the integral of \(\textbf{J}\) throughout the cylinder. In a more general geometry, in which \(\textbf{J}\) is not necessarily perpendicular to the area of interest, and indeed in which the area need not be planar, this would be \(\int \textbf{J} \cdot \textbf{d}\boldsymbol{\sigma}\).
Now for the less obvious component to the "enclosed current". See Figure XV.2.
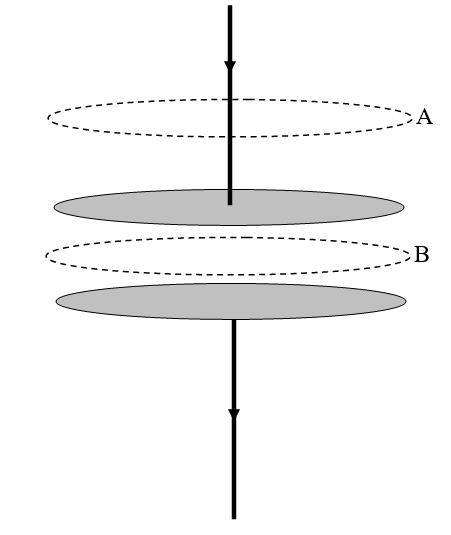
FIGURE XV.2
In Figure XV.2, I imagine two capacitor plates in the process of being charged. There is undoubtedly a current flowing in the connecting wires. There is a magnetic field at A, and the line integral of the field around the upper dotted curve is undoubtedly equal to the enclosed current. The current is equal to the rate at which charge is being built up on the plates. Electrons are being deposited on the lower plate and are leaving the upper plate. There is also a magnetic field at B (it doesn't suddenly stop!), and the field at \(B\) is just the same as the field at A, which is equal to the rate at which charge is being built up on the plates. The charge on the plates (which may not be uniform, and indeed won't be while the current is still flowing or if the plates are not infinite in extent) is equal to the integral of the charge density times the area. And the charge density on the plates, by Gauss's theorem, is equal to the electric field \(\textbf{D}\) between the plates. Thus the current is equal to the integral of \(\dot{ \textbf{D}}\) over the surface of the plates. Thus the line integral of \(\textbf{H}\) around either of the dashed closed loops is equal to \(\int \dot{\textbf{D}} \cdot \textbf{d} \boldsymbol{\sigma}\).
In general, both types of current (the obvious one in which there is an obvious flow of charge, and the less obvious one, where the electric field is varying because of a real flow of charge elsewhere) contributes to the magnetic field, and so Ampère's theorem in general must read
\[ \int_{loop} \textbf{H} \cdot \textbf{ds} = \int_{area} (\dot{ \textbf{D}} + \textbf{J}) \cdot \textbf{d}\boldsymbol{\sigma} \tag{15.5.1} \label{15.5.1}\]
But the line integral of a vector field around a closed plane curve is equal to the surface integral of its curl, and therefore
\[ \int_{area} \text{curl} \, \textbf{H} \cdot d{\sigma} = \int_{area} (\dot{ \textbf{D}} + \textbf{J}) \cdot \textbf{d} \boldsymbol{\sigma} \tag{15.5.2} \label{15.5.2}\]
Thus we arrive at:
\[\text{curl}\, \textbf{H} = \dot{ \textbf{D}} + \textbf{J}\tag{15.5.3} \label{15.5.3}\]
or, in the nabla notation,
\[\boldsymbol{\nabla} \times \textbf{H} = \dot {\textbf{D}} + \textbf{J}\tag{15.5.4} \label{15.5.4}\]
This is the third of Maxwell's equations.


