2.5: A Point Charge and a Conducting Sphere
- Page ID
- 5421
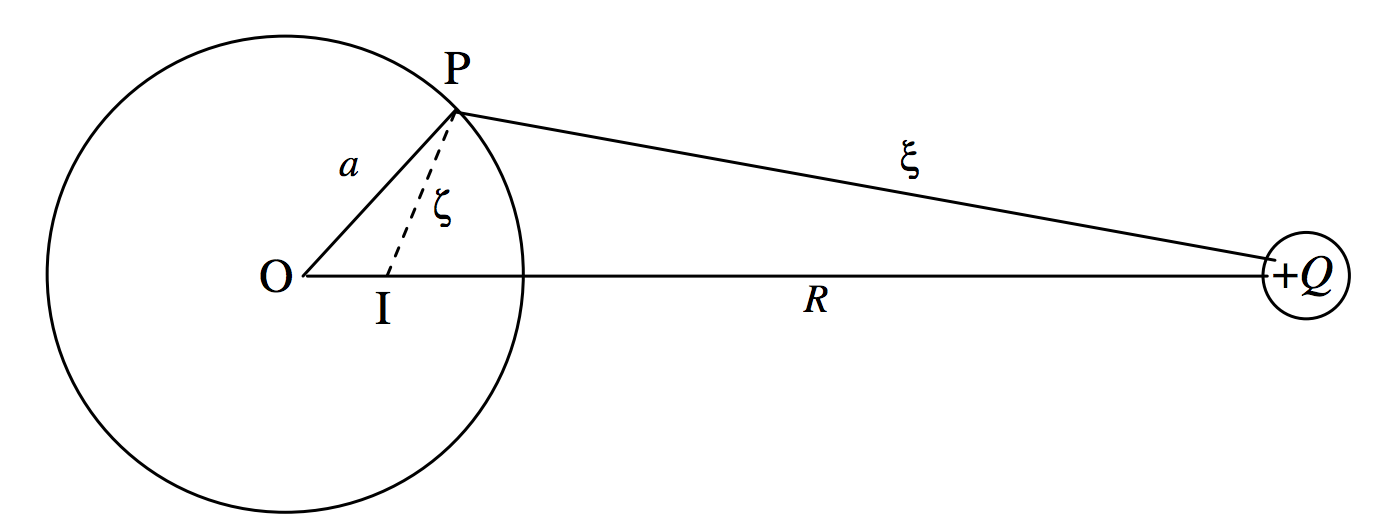
\(\text{FIGURE II.3}\)
A point charge + \(Q\)is at a distance \(R\) from a metal sphere of radius \(a\). We are going to try to calculate the surface charge density induced on the surface of the sphere, as a function of position on the surface. We shall bear in mind that the surface of the sphere is an equipotential surface, and we shall take the potential on the surface to be zero.
Let us first construct a point I such that the triangles OPI and PQO are similar, with the lengths shown in Figure \(II\).3. The length OI is \(a^2 /R\). Then \(R/ξ = a/ζ\), or
\[\label{2.5.1}\dfrac{1}{ξ}-\dfrac{a/R}{ζ}=0\]
This relation between the variables \(ξ \text{ and }ζ\) is in effect the equation to the sphere expressed in these variables.
Now suppose that, instead of the metal sphere, we had (in addition to the charge + \(Q\) at a distance \(R\) from O), a second point charge −\((a/R) Q\text{ at }I\). The locus of points where the potential is zero is where
\[\label{2.5.2}\dfrac{Q}{4\pi\epsilon_0}\left ( \dfrac{1}{ξ}-\dfrac{a/R}{ζ}\right ) = 0\]
That is, the surface of our sphere. Thus, for purposes of calculating the potential, we can replace the metal sphere by an image of \(Q\) at \(I\), this image carrying a charge of \(−(a/R)Q\).
Let us take the line OQ as the \(z\)-axis of a coordinate system. Let \(X\) be some point such that OX = \(r\) and the angle XOQ= \(θ\). The potential at P from a charge +\(Q\) at \(Q\) and a charge −\((a/R)Q\) at \(I\) is (see Figure \(II\).4)
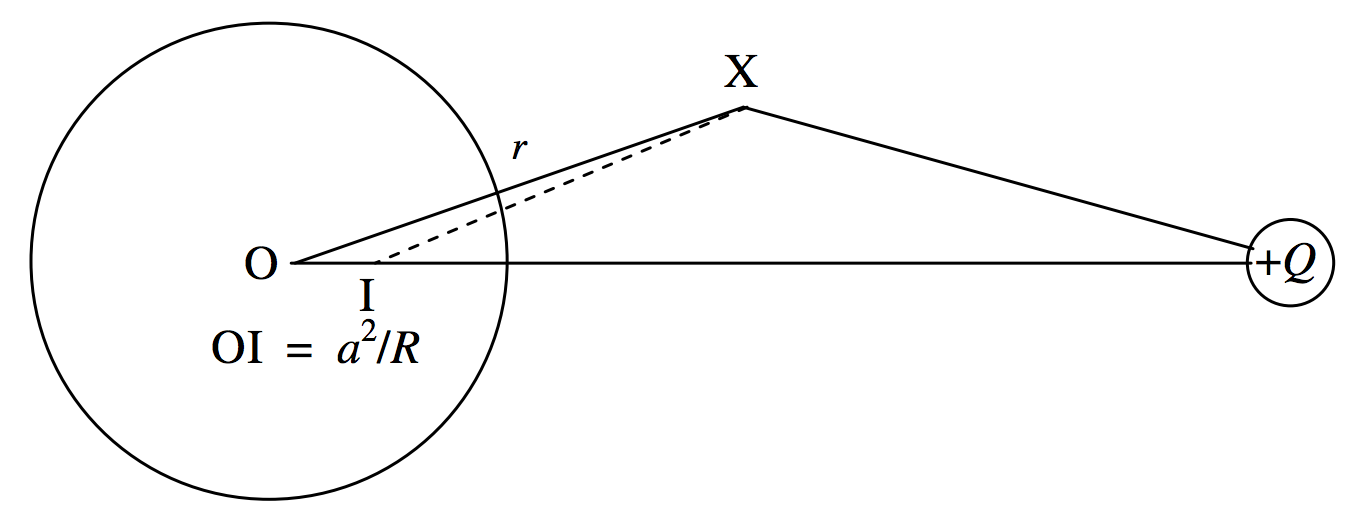
\(\text{FIGURE II.4}\)
\[\nonumber V=\dfrac{q}{4\pi\epsilon_0}\left (\dfrac{1}{(r^2+R^2-2rR\cos \theta)^{1/2}}-\dfrac{a/R}{(r^2+a^/R^2 -2a^2r\cos \theta /R)^{1/2}}\right )\]
The E field on the surface of the sphere is \(−∂V / ∂r\) evaluated at \(r = a\). The \(D\) field is \(\epsilon_0\) times this, and the surface charge density is equal to \(D\). After some patience and algebra, we obtain, for a point \(X\) on the surface of the sphere
\[\label{2.5.3}\sigma = -\dfrac{Q}{4\pi}\dfrac{R^2-a^2}{a}\cdot \dfrac{1}{(XQ)^3}\]


