4.14: Tortures for the Brain
- Page ID
- 5980
I don’t know if any of the examples in this section have any practical applications, but they are excellent ways for torturing students, or for whiling away rainy Sunday afternoons.
Q4.14.1
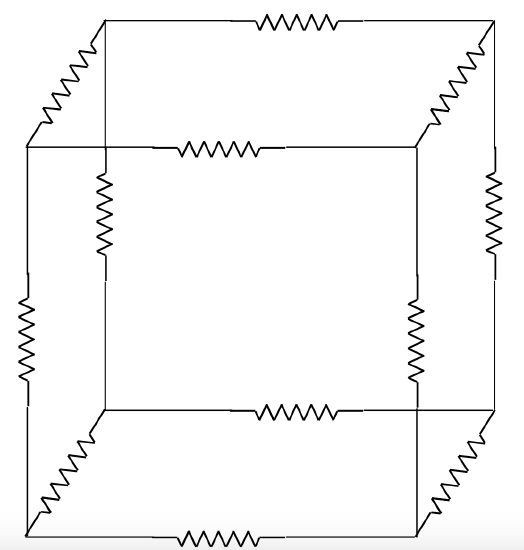
The drawing shows 12 resistances, each of value r \(\Omega\), arranged along the edges of a cube. What is the resistance across opposite corners of the cube?
Q4.14.2
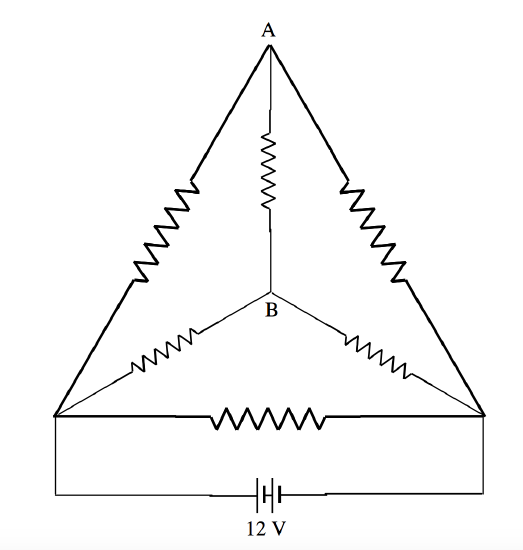
The drawing shows six resistors, each of resistance 1 \(\Omega\), arranged along the edges of a tetrahedron. A 12 V battery is connected across one of the resistors. Calculate the current between points A and B.
Q4.14.3
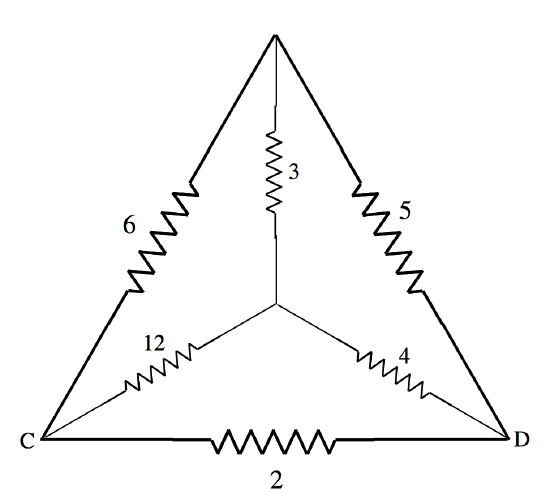
The Figure shows six resistors, whose resistances in ohms are marked, arranged along the edges of a tetrahedron. Calculate the net resistance between C and D.
Q4.14.4
R1 = 8 \(\Omega\) and R2 = 0.5 \(\Omega\) are connected across a battery. The rate at which heat is generated is the same whether they are connected in series or in parallel. What is the internal resistance r of the battery?
Q4.14.5
R1 = 0.25 \(\Omega\) and R2 = ? are connected across a battery whose internal resistance r is 0.5 \(\Omega\). The rate at which heat is generated is the same whether they are connected in series or in parallel. What is the value of R2?
Q4.14.6
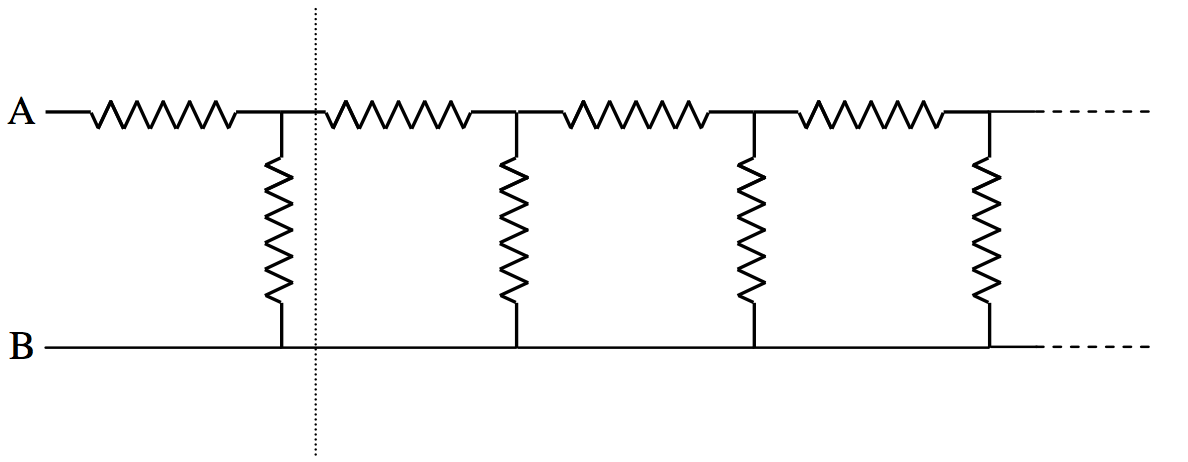
In the above circuit, each resistance is 1 ohm. What is the net resistance between A and B if the chain is of infinite length?
Q4.14.7
What is the resistance between A and B in question 4.14.6 if the chain is not of infinite length, but has n “links” – i.e. 2n resistors in all?
Q4.14.8
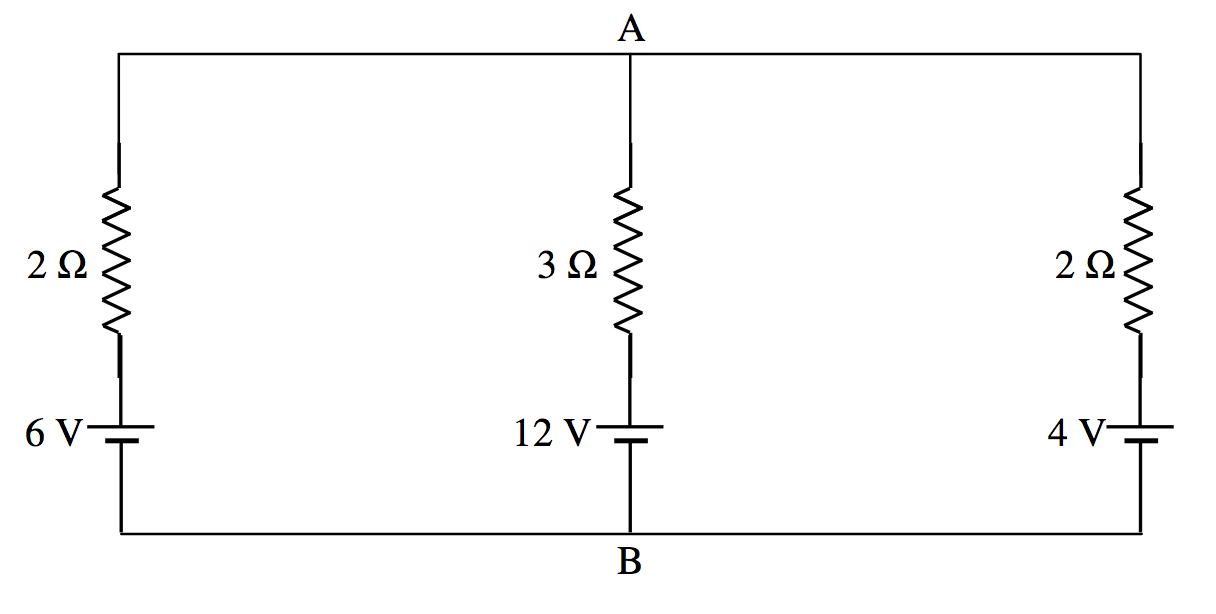
In the circuit below, what is the potential difference between A and B, and what is the current in each resistor?