8.4: Charged Particle in an Electric and a Magnetic Field
- Page ID
- 5462
The force on a charged particle in an electric and a magnetic field is
\[\textbf{F} = q(\textbf{E} +\textbf{v} \times \textbf{B}). \label{8.4.1}\]
As an example, let us investigate the motion of a charged particle in uniform electric and magnetic fields that are at right angles to each other. Specifically, let us choose axes so that the magnetic field \(\textbf{B}\) is directed along the positive \(z\)-axis and the electric field is directed along the positive \(y\)-axis. (Draw this on a large diagram!) Try and imagine what the motion would be like. Suppose, for example, the motion is all in the \(xy\)-plane. Perhaps the particle will move round and round in a circle around an axis parallel to the magnetic field, but the centre of this circle will accelerate in the direction of the electric field. Well, you are right in that the particle does move in a circle around an axis parallel to \(\textbf{B}\), and also that the centre of the circle does indeed move. But the rest of it isn't quite right. Before embarking on a mathematical analysis, see if you can imagine the motion a bit more accurately.
We'll suppose that at some instant the \(x\), \(y\) and \(z\) components of the velocity of the particle are \(u\), \(v\) and \(w\). We'll suppose that these velocity components are all nonrelativistic, which means that m is constant and not a function of the speed. The three components of the equation of motion (Equation \ref{8.4.1}) are then
\[m\dot u = qBv,\]
\[m \dot v = -qBu + qE\]
and
\[m \dot w = 0.\]
For short, I shall write \(q \ B/m = \omega\) (the cyclotron angular speed) and, noting that the dimensions of \(E/B\) are the dimensions of speed (verify this!), I shall write \(E/B = V_D\), where the significance of the subscript \(D\) will become apparent in due course. The equations of motion then become
\[\ddot x = \dot u = \omega v,\]
\[\ddot y = \dot v = -\omega (u-V_D)\]
and
\[\ddot z = \dot w =0.\]
To find the general solutions to these, we can, for example, let \(X = u − V_D\). Then equations 8.4.5 and 8.4.6 become \(\dot X =\omega v\) and \(\dot v =-\omega X\). From these, we obtain \(\ddot X = -\omega^2 X\). The general solution of this is \(X = A \sin (\omega t + \alpha)\), and so \(u=A \sin (\omega t + \alpha)+V_D\). By integration and differentiation with respect to time we can find \( x\) and \(\ddot x\) respectively. Thus we obtain:
\[x = -\frac{A}{\omega} \cos (\omega t +\alpha) +V_Dt + D,\]
\[u= \dot x = A \sin (\omega t +\alpha) + V_D\]
and
\[\ddot x = A \omega \cos (\omega t +\alpha).\]
Similarly we can solve for y and z as follows:
\[y=\frac{A}{\omega}\sin (\omega t + \alpha) + F,\]
\[v = \dot y = A\cos (\omega t + \alpha),\]
\[\ddot y = -A\omega \sin (\omega t +\alpha),\]
\[z=w_0t+ z_0,\]
\[w=\dot z = w_0\]
and \[\ddot z=0.\]
There are six arbitrary constants of integration, namely \(A\), \(D\), \(F\), \(\alpha\), \(z_0\) and \(w_0\), whose values depend on the initial conditions (position and velocity at \(t = 0\)). Of these, \(z_0\) and \(w_0\) are just the initial values of \(z\) and \(w\). Let us suppose that these are both zero and that all the motion takes place in the \(xy\)-plane.
In these equations \(A\) and \(\alpha\) always occur in the combinations \(A \sin \alpha\) and \(A \cos \alpha\), and therefore for convenience I am going to let \(A \sin \alpha = S\) and \(A \cos \alpha = C\), and I am going to re-write equations 8.4.8, 8.4.9, 8.4.11 and 8.4.12 as
\[x=-\frac{1}{\omega} (C \cos \omega t - S \sin \omega t) + V_Dt+D,\]
\[u=C\sin \omega t +S\cos \omega t + V_D,\]
\[y=\frac{1}{\omega}(C\sin \omega t + S \cos \omega t) + F,\]
and \[v= C \cos \omega t - S \sin \omega t.\]
Let us suppose that the initial conditions are: at \(t = 0\), \(x = y = u = v = 0\). That is, the particle starts from rest at the origin. If the put these initial conditions in equations 8.4.17-20, we find that \(C = 0\), \(S = −V_D\), \(D = 0\) and \(F = V_D/\omega\). Equations 8.4.17 and 8.4.19, which give the equation to the path described by the particle, become
\[x=-\frac{V_D}{\omega} \sin \omega t + V_D t\]
and \[y=\frac{V_D}{\omega}(1-\cos \omega t).\]
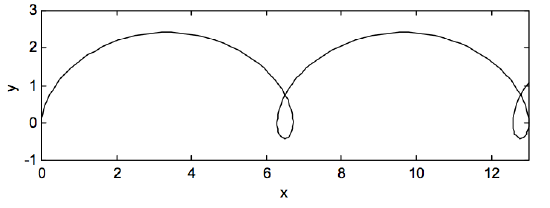
It is worth reminding ourselves here that the cyclotron angular speed is \(\omega = qB/m\) and that \(V_D = E/B\), and therefore \(\frac{V_D}{\omega}=\frac{mE}{qB^2}\). These equations are the parametric equations of a cycloid. (For more on the cycloid, see Chapter 19 of the Classical Mechanics notes in this series.) The motion is a circular motion in which the centre of the circle drifts (hence the subscript \(D\)) in the \(x\)-direction at speed \(V_D\). The path is shown in Figure \(\text{VIII.2}\), drawn for distances in units of \(\frac{V_D}{\omega}=\frac{mE}{qB^2}\).
\(\text{FIGURE VII.2}\)
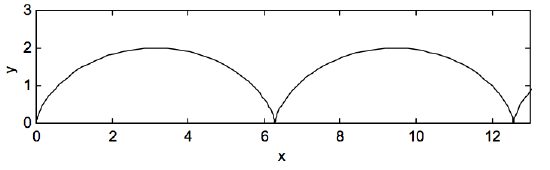
I leave it to the reader to try different initial conditions, such as one of \(u\) or \(v\) not initially zero. You can try with \(u_0\) or \(v_0\) equal to some multiple of fraction of \(V_D\), and you can make the \(u_0\) or \(v_0\) positive or negative. Calculate the values of the constants \(D\), \(F\), \(C\) and \(S\) and draw the resulting path. You will always get some sort of cycloid. It may not be a simple cycloid as in our example, but it might be an expanded cycloid (i.e. small loops instead of cusps) or a contracted cycloid, which has neither loops nor cusps, but looks more or less sinusoidal. I’ll try just one. I’ll let \(u_0 = 0\) and \(v_0 = +V_D\). If I do that, I get
\[x=\frac{V_D}{\omega}(1-\cos \omega t - \sin \omega t)+V_Dt\]
and \[y=\frac{V_D}{\omega}(1-\cos \omega t + \sin \omega t).\]
This looks like this:
\(\text{FIGURE VII.3}\)