7.4: Discrete Symmetries
- Page ID
- 15041
Let us first look at the key discrete symmetries – parity \(P\) (space inversion) charge conjugation \(C\) and time-reversal \(T\).
Parity \(P\)
Parity is the transformation where we reflect each point in the origin, \({\vec{x}} \rightarrow -{\vec{x}}\) (Figure Figure \(\PageIndex{1}\)). This transformation should be familiar to you.
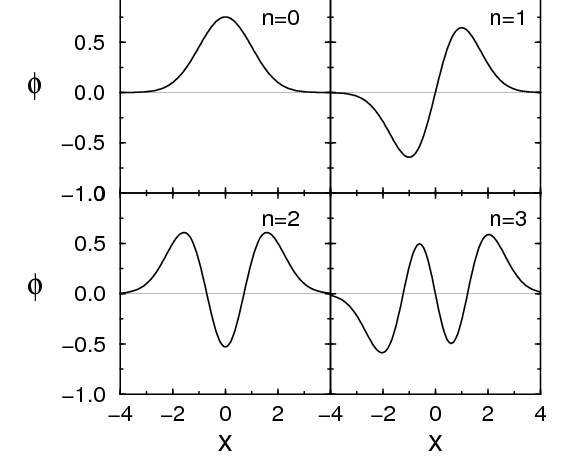
Let us think of the one dimensional harmonic oscillator, with Hamiltonian
\[-\frac{\hbar^2}{2m} \frac{d}{dx^2} + \dfrac{1}{2} m \omega^2 x^2.\]
The Hamiltonian does not change under the substitution \(x \rightarrow -x\). The well-known eigenstates to this problem are either even or odd under this transformation, see Figure \(\PageIndex{1}\), and thus have either even or odd parity,
\[P \psi(x,t) = \psi(-x,t) = \pm\psi(x,t),\]
where \(P\) is the transformation that take \(x \rightarrow -x\). For \[P \psi(x,t) =\psi(x,t)\] we say that the state has even parity, for the minus sign we speak about negative parity. These are the only two allowed eigenvalues, as can be seen from looking at the probability density \(|\psi(x,y)|^2\). Since this must be invariant, we find that
\[|\psi(x,y)|^2=|P\psi(x,y)|^2\]
which shows that the only real eigenvalues for \(P\) are \(\pm 1\). One can show that there is a relation between parity and the orbital angular momentum quantum number \(L\), \(\pi=(-1)^L\), which relates two space-time symmetries.
It is found, however, that parity also has an intrinsic part, which is associated with each type of particle. A photon (\(\gamma\)) has negative parity. This can be understood from the following classical analogy. When we look at Maxwell’s equation for the electric field,
\[{\vec{\nabla}}\cdot {\vec{E}}(x,t) = \frac{1}{\epsilon_0}\rho(x,t), \label{eq:maxwell}\]
we find that upon reversal of the coordinates this equation becomes
\[-{\vec{\nabla}}\cdot {\vec{E}}(-x,t) = \frac{1}{\epsilon_0}\rho(-x,t).\]
The additional minus sign, which originates in the change of sign of \(\nabla\) is what gives the electric field and thus the photon its negative intrinsic parity.
We shall also wish to understand the parity of particles and antiparticles. For fermions (electrons, protons, …) we have the interesting relation \(P_f P_{\bar f}=-1\), which will come in handy later!
Charge conjugation \(C\)
The name of this symmetry is somewhat of a misnomer. Originally it stems from QED, where it was found that a set of interacting electrons behaves exactly the same way as a similar set of positrons. So if we change the sign of all charges the dynamics is the same. Actually, the symmetry generalises a little bit, and in general refers to a transformation where we change all particles in their antiparticles.
Once again we find \(C^2=1\), and the only possible eigenvalues of this symmetry are \(\pm 1\). An uncharged particle like the photon that is its own antiparticle, must be an eigenstate of the symmetry operation, and it is found that it has eigenvalue \(-1\),
\[C \psi_\gamma = - \psi_\gamma.\]
(Here \(\psi_\gamma\) is the wave function of the photon.) This can be shown from Maxwell’s Equation \ref{eq:maxwell} as before, since \(\rho\) changes sign under charge conjugation.
For a combination of a particle and an antiparticle, we find that \(C_{f} C_{\bar f}=-1\) for fermions, and \(+1\) for bosons.
Time reversal \(T\)
On a microscopic scale it is not very apparent whether time runs forward or backwards, the dynamics where we just change the sign of time is equally valid as the original one. This corresponds to flipping the sign of all momenta in a Feynman diagram, so that incoming particles become outgoing particles and vice-versa. This symmetry is slightly nastier, and acts on both space-time and intrinsic quantities such as spin in a complicated way. The space time part is found to be
\[T \psi({\vec{r}}, t) = \psi^*({\vec{r}}, -t).\]
Combined with its intrinsic part we find that it has eigenvalues \(\pm i\) for fermions (electrons, etc.) and \(\pm 1\) for bosons (photons, etc.).


