8.3: The quark model of strong interactions
- Page ID
- 15047
Once the eightfold way (as the SU(3) symmetry was poetically referred to) was discovered, the race was on to explain it. As I have shown before the decaplet and two octets occur in the product \[{\mathbf{3}} \otimes {\mathbf{3}} \otimes {\mathbf{3}} = {\mathbf{1}} \oplus {\mathbf{8} }\oplus {\mathbf{8}} \oplus{\mathbf{10}}.\] A very natural assumption is to introduce a new particle that comes in three “flavours” called up, down and strange (\(u\), \(d\) and \(s\), respectively), and assume that the baryons are made from three of such particles, and the mesons from a quark and anti-quark (remember,| =.) Each of these quarks carries one third a unit of baryon number. The properties can now be tabulated (Table \(\PageIndex{1}\)).
| Quark | label | spin | \(Q/e\) | \(I\) | \(I_3\) | \(S\) | \(B\) |
|---|---|---|---|---|---|---|---|
| Up | \(u\) | \(\frac{1}{2}\) | \(+\frac{2}{3}\) | \(\frac{1}{2}\) | +\(\frac{1}{2}\) | 0 | \(\frac{1}{3}\) |
| Down | \(d\) | \(\frac{1}{2}\) | \(-\frac{1}{3}\) | \(\frac{1}{2}\) | -\(\frac{1}{2}\) | 0 | \(\frac{1}{3}\) |
| Strange | \(s\) | \(\frac{1}{2}\) | \(-\frac{1}{3}\) | \(0\) | \(0\) | -1 | \(\frac{1}{3}\) |
In the multiplet language I used before, we find that the quarks form a triangle, as given in Figure \(\PageIndex{1}\).
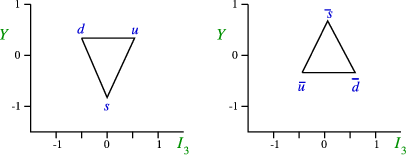
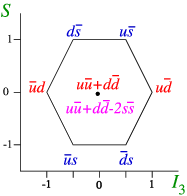
Once we have made this assignment, we can try to derive what combination corresponds to the assignments of the meson octet, Figure \(\PageIndex{2}\). We just make all possible combinations of a quark and antiquark, apart from the scalar one \(\eta'=u\bar{u}+d\bar{d} +c\bar{c}\) (why?).
A similar assignment can be made for the nucleon octet, and the nucleon decaplet, see e.g., see FFigure \(\PageIndex{3}\).



