3.2: Moment of Force

Last updated
Save as PDF

Page ID: 6940

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

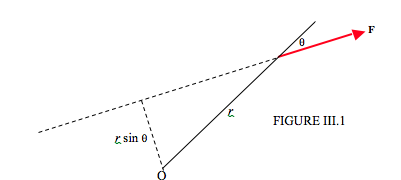
First, let’s look at a familiar two-dimensional situation. In Figure III.1 I draw a force \(\textbf{F}\) and a point O. The moment of the force with respect to O can be defined as

Force times perpendicular distance from O to the line of action of \(\textbf{F}\).

alt

Alternatively, (Figure III.2) the moment can be defined equally well by

Transverse component of force times distance from O to the point of application of the force.

alt

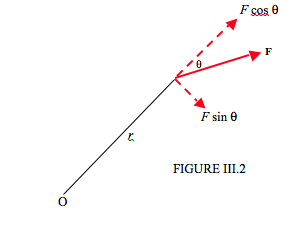
Either way, the magnitude of the moment of the force, also known as the torque, is \(rF \sin\theta\) We can regard it as a vector, \( \boldsymbol\tau \), perpendicular to the plane of the paper:

\begin{equation} \ \boldsymbol\tau = \textbf{r} \times \textbf{F}\tag{3.2.1}\label{eq:3.2.1} \end{equation}

Now let me ask a question. Is it correct to say the moment of a force with respect to (or “about”) a point or with respect to (or “about”) an axis?

In the above two-dimensional example, it does not matter, but now let me move on to three dimensions, and I shall try to clarify.

In Figure III.3, I draw a set of rectangular axes, and a force \(\textbf{F}\), whose position vector with respect to the origin is \(\textbf{r}\).

alt

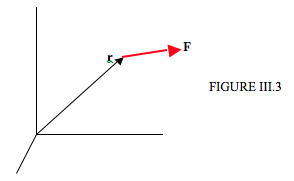
The moment, or torque, of \(\textbf{F}\) with respect to the origin is the vector

\begin{equation} \ \boldsymbol\tau = \textbf{r}\times \textbf{F}\tag{3.2.2}\label{eq:3.2.2} \end{equation}

The \( x-, y-\) and \( z\) -components of \( \boldsymbol\tau \) are the moments of \(\textbf{F}\) with respect to the \(x-, y-\) and z-axes. You can easily find the components of \( \boldsymbol\tau \) by expanding the cross product \( \ref{eq:3.2.2}\):

\[ \boldsymbol\tau = \hat{\textbf{x}}(yF_{z}-zF_{y})+\hat{\textbf{y}}(yF_{x}-xF_{z})+\hat{\textbf{z}}(xF_{y}-yF_{x}) \tag{3.2.3}\label{eq:3.2.3} \]

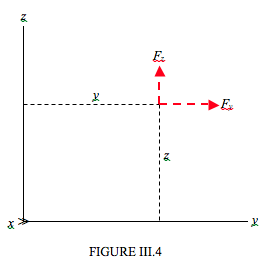
where \( \bf \hat{x},\hat{y},\hat{z}\) are the unit vectors along the \( x,y,z\) axes. In Figure III.4, we are looking down the \( x\)-axis, and I have drawn the components \( F_{y}\) and \( F_{z}\), and you can see that, indeed, \( \tau_{x} =yF_{z}-zF_{y}\).

alt

The dimensions of moment of a force, or torque, are ML²T^-2, and the SI units are N m. (It is best to leave the units as N m rather than to express torque in joules.)