1.2: Plane Triangular Lamina
- Page ID
- 6926
Definition: A median of a triangle is a line from a vertex to the midpoint of the opposite side.
Theorem I. The three medians of a triangle are concurrent (meet at a single, unique point) at a point that is two-thirds of the distance from a vertex to the midpoint of the opposite side.
Theorem II. The centre of mass of a uniform triangular lamina (or the centroid of a triangle) is at the meet of the medians.
The proof of I can be done with a nice vector argument (Figure I.1):
Let \(\bf{\text{A}}\) , \( \bf{\text{B}}\) be the vectors \( \text{OA}\) , \( \text{OB}\) . Then \( \bf{\text{A+B}}\) is the diagonal of the parallelogram of which \( OA\) and \( \text{OB}\) are two sides, and the position vector of the point \( \text{C}_{1}\) is \( \frac{1}{3}(\bf{\text{A+B}})\) .
To get \( \text{C}_{2}\), we see that
\( {\bf C}_2 = {\bf A} + \dfrac{2}{3}(\text{AM}_2) = {\bf A} + \dfrac{2}{3}({\bf M_2 - A}) = {\bf A} + \dfrac{2}{3}(\dfrac{1}{2}{\bf B- A}) = \dfrac{1}{3}( {\bf A+B})\)
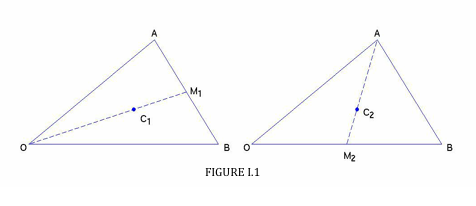
Thus the points \( \text{C}_{1}\) and \( \text{C}_{2}\) are identical, and the same would be true for the third median, so Theorem I is proved.
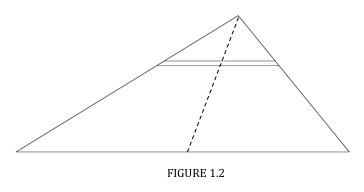
Now consider an elemental slice as in Figure I.2. The centre of mass of the slice is at its mid-point. The same is true of any similar slices parallel to it. Therefore the centre of mass is on the locus of the mid-points - i.e. on a median. Similarly, it is on each of the other medians, and Theorem II is proved.
That needed only some vector geometry. We now move on to some calculus.


