15.18: Doppler Effect
- Page ID
- 8471
It is well known that the formula for the Doppler effect in sound is different according to whether it is the source or the observer that is in motion. An answer to the question “Why should this be?” to the effect that “Oh, that’s just the way the algebra works out” is obviously unsatisfactory, so I shall try to explain why, physically, there is a difference. Then, when you have thoroughly understood that observer in motion is an entirely different situation from source in motion, and the formulas must be different, we shall look at the Doppler effect in light, and we’ll return to square one when we find that the formulas for source in motion and observer in motion are the same!
This section on the Doppler effect will probably be rather longer than it need be, just because some aspects interested me – but if you find it too long, just skip the parts that aren’t of special interest to you. These will quite likely include the parts on the ballistic Doppler effect.
First, we’ll deal with the Doppler effect in sound. All speeds are supposed to be very small compared with the speed of light, so that we need not trouble ourselves with Lorentz transformations. First, let’s deal with observer in motion (Figure XV. 24).
When the source is at rest, it emits concentric equally-spaced spherical wavefronts at some frequency. When an observer moves towards the source, he will pass these wavefronts at a higher frequency that the frequency at which they were emitted, and that is the cause of the Doppler effect with a stationary source and moving observer.
Now, we’ll look at the source-in-motion situation. (Figure XV.25).
Here we see that the wavefronts are not equally spaced, but are compressed ahead of the motion of the source, and for that reason they will pass a stationary observer at a higher frequency than the frequency at which they were emitted. Thus the nature of the effect is a little different according to whether it is the source or the observer that is in motion, and thus one would not expect identical equations to describe the two situations.
We shall move on shortly to discuss the effect quantitatively and develop the relevant equations. I shall assume that the reader is familiar with the usual relation connecting wavelength, frequency and speed of a wave. Nevertheless I shall write down the relation in large print, three times, just to make sure:
SPEED = FREQUENCY % WAVELENGTH
FREQUENCY = SPEED ÷ WAVELENGTH
WAVELENGTH = SPEED ÷ FREQUENCY
I am going to start with the Doppler effect in sound, where the speed of the signal is constant with respect to the medium than transmits the sound – usually air. I shall give the necessary formulas for source and observer each in motion. If you want the formulas for one or the other stationary, you just put one of the speeds equal to zero. The speeds of the source \( S\) and of the observer \( O\) relative to the air will be denoted respectively by \( \nu_{1}\) and \( \nu_{2}\) and the speed of sound in air will be denoted by \( c\). The situation is shown in Figure XV.26.
The relevant formulas are shown below:
The way we work this table is just to follow the arrows. Starting at the top left, we suppose that the source emits a signal of frequency \( \nu_{0}\). The speed of the signal relative to the source is \( c-v_{1}\), and so the wavelength is \( \frac{(c-v_{1})}{\nu_{0}}\). The wavelength is the same for the observer (we are supposing that all speeds are very much less than the speed of light, so the Lorentz factor is effectively 1.) The speed of sound relative to the observer is \( c-v_{2}\), and so the frequency heard by the observer is the last (upper right) entry of the table.
Two special cases:
a. Observer in motion and approaching a stationary source at speed \( v\). \( v_{1}= 0 \) and \( v_{2}=-v\). In that case the frequency heard by the observer is
\[ \nu=\nu_{0}(1+\frac{v}{c}). \label{15.18.1} \]
b. Source in motion and approaching a stationary observer at speed \( v\). \( v_{1}=v\) and \( v_{2}=0\). In that case the frequency heard by the observer is
\[ \nu=\frac{\nu_{0}}{(1-\frac{v}{c})}\approx\nu_{0}(1+(\frac{v}{c})+(\frac{v}{c})^{2}+...). \label{15.18.2} \]
We might now consider reflection. Thus, suppose you approach a brick wall at speed \( v\) while whistling a note of frequency \( \nu_{0}\). What will be the frequency of the echo that you hear? Let’s make the question a little more general. A source \( S\), emitting a whistle of frequency \( \nu_{0}\), approaches a brick wall M at speed \( v_{1}\). A separate observer O approaches the wall (from the same side) at speed \( v_{2}\). And, for good measure, let’s have the brick wall moving at speed \( v_{3}\). (The reader may notice at this point that theoretical physics is rather easier than experimental physics.) The situation is shown in Figure XV.27.
We construct a table similar to the previous one.
At all times, the speed relative to the air is \( c\).
The answer to our initial question, in which the source and the observer were one and the same, and the mirror (wall) was stationary is found by putting \( v_{1}= v_{2}=v\) and \( v_{3}=0\) in the last (top right) formula in the table. This results in
\[ \nu = \nu_{0} \left( \frac{c+v}{c-v}\right) \approx \nu_{0}(1+2(\frac{v}{c})+2(\frac{v}{c})^{2}+2(\frac{v}{c})^{3}...). \label{15.18.3} \]
So much for the Doppler effect in sound. Before moving on to light, I want to look at what I shall call the Doppler effect in ballistics, or “cops and robbers”. An impatient reader may safely skip this discussion of ballistic Doppler effect. A police (“cop”) car is chasing a stolen car driven by robbers. The cop car is the “source” and the robber’s car (or, rather the car that they have stolen, for it is not theirs) are the “observers”. The cop car (“source”) is travelling at speed \( v_{1}\) and the robbers (“observer”) is travelling at speed \( v_{2}\). The cops are firing bullets (the “signal”) towards the robbers. (No one gets hurt in this thought experiment, which is all make-believe.) The bullets leave the muzzle of the revolver at speed \( c\)(that is the speed of the bullets, and is nothing to do with light) relative to the revolver, and hence they travel (relative to the lamp-posts at the side of the road) at speed \( c+v_{1}\) and relative to the robbers at speed \( c+v_{1}-v_{2}\). The cops fire bullets at frequency \( \nu_{0}\), and our task is to find the frequency with which the bullets are “received” by the robbers. The distance between the bullets is the “wavelength”.
This may not be a very important exercise, but it is not entirely pointless, for fairness dictates that, when we are considering (even if only to discard) possible plausible mechanisms for the propagation of light, we might consider, at least briefly, the so-called “ballistic” theory of light propagation, in which the speed of light through space is equal to the speed at which it leaves the source plus the speed of the source. Some readers may be aware of the Michelson-Morley experiment. That experiment demonstrated that light was not propagated at a speed that was constant with respect to some all-pervading “luminiferous aether” – but it must be noted that it did nothing to prove or disprove the “ballistic” theory of light propagation, since it did not measure the speed of light from moving sources. In the intervening years, some attempts have indeed been made to measure the speed of light from moving sources, though their interpretation has not been free from ambiguity.
I now construct a table showing the “frequency”, “speed” and “wavelength” for ballistic propagation in exactly the same way as I did for sound.
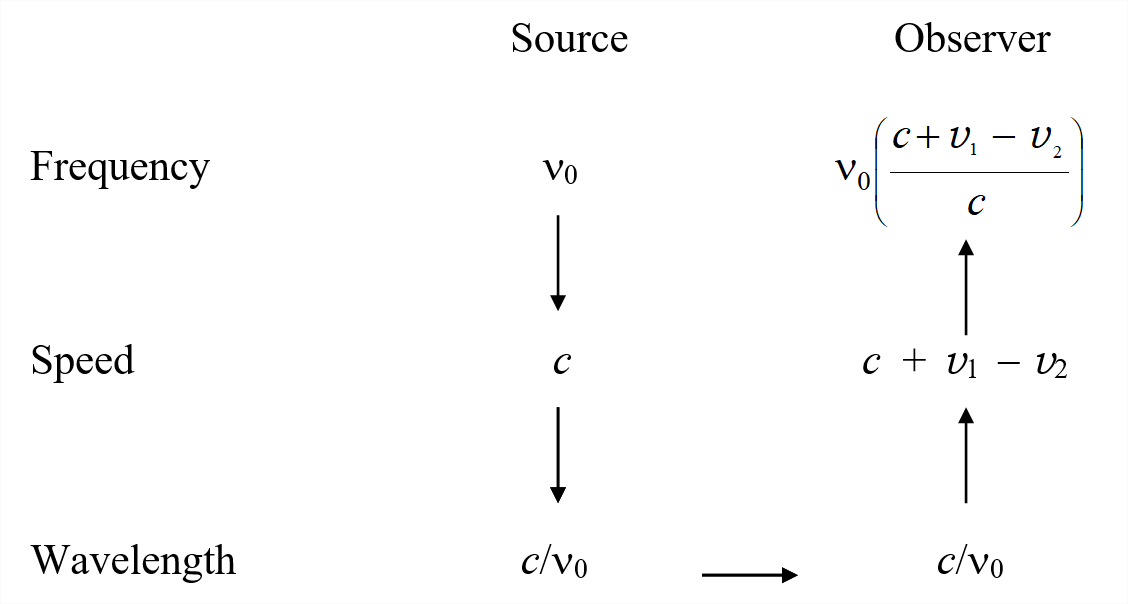
In order not to spend longer on “ballistic” propagation than is warranted by its importance, I’ll just let the reader spend as much or as little time pondering over this table as he or she wishes. Just one small point might be noted, namely that the formulas for “observer in motion” and “source in motion” are the same.
For completeness rather than for any important application, I shall also construct here the table for “reflection”. A source of bullets is approaching a mirror at speed \( v_{1}\). An observer is also approaching the mirror, from the same side, at speed \( v_{2}\). And the mirror is moving at speed \( v_{3}\), and reflection is elastic (the coefficient of restitution is 1.) You are free to put as many of these speeds equal to zero as you wish.
The entries for “speed” give the speed relative to the source or mirror or observer. The speed relative to stationary lampposts at the side of the road is \( c+v_{1}\) before reflection and \( c+v_{1}-2v_{3}\) after reflection.
We now move on to the only aspect of the Doppler effect that is really relevant to this chapter, namely the Doppler effect in light. In the previous two situations I have been able to assume that all speeds were negligible compared with the speed of light, and we have not had to concern ourselves with relativistic effects. Here, however, the signal is light and is propagated at the speed of light, and this speed is the same whether referred to the reference frame in which the source is stationary or the observer is stationary. Further, the Doppler effect is noticeable only if source or observer are moving at speeds comparable to that of light. We shall see that the difference between the frequency of a signal relative to an observer and the frequency relative to the source is the result of two effects, which, while they may be treated separately, are both operative and in that sense inseparable. These two effects are the Doppler effect proper, which is a result of the changing distance between source and observer, and the relativistic dilation of time.
I am going to use the symbol \( T\) to denote the time interval between passage of consecutive crests of an electromagnetic wave. I’ll call this the period. This is merely the reciprocal of the frequency \( \nu\). I am going to start by considering a situation in which a source and an observer a receding from each other at a speed \( v\). I have drawn this in Figure XV.27, which is referred to a frame in which the observer is at rest. The speed of light is \( c\).
Let us suppose that \( S\) emits an electromagnetic wave of period \( T_{0}=\frac{1}{\nu_{0}}\) referred to the frame in which \( S\) is at rest. We are going to have to think about four distinct periods or frequencies:
1. The time interval between the emission of consecutive crests by \( S\) referred to the reference frame in which \( S\) is at rest. This is the period \( T_{0}\) and the frequency \( \nu_{0}\) that we have just mentioned.
2. The time interval between the emission of consecutive crests by \( S\) referred to the reference frame in which \( O\) is at rest. By the relativistic formula for the dilation of time this is
\[ \gamma T_{0} \quad or \quad \frac{T_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}. \label{15.18.4} \]
3. The time interval between the reception of consecutive crests by \( O\) as a result of the increasing distance between \( O\) and \( S\) (the “true” Doppler effect, as distinct from time dilation) referred to the reference frame in which \( S\) is at rest. This is
\[ T_{0}(1+\frac{v}{c}). \label{15.18.5} \]
4. The time interval between the reception of consecutive crests by \( O\) as a result of the increasing distance between \( O\) and \( S\) (the “true” Doppler effect, as distinct from time dilation) referred to the reference frame in which \( O\) is at rest. This is
\[ \gamma \quad \text{times} \quad T_{0}\left(1+\frac{v}{c}\right). \label{15.18.6} \]
This, of course, is what \( O\) “observes”, and, when you do the trivial algebra, you find that this is
\[ T=T_{0}\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}, \label{15.18.7} \]
or, in terms of frequency,
\[ \nu=\nu_{0}\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}. \label{15.18.8} \]
If source and observer approach each other at speed \( v\), the result is
\[ \nu=\nu_{0}\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}. \label{15.18.9} \]
The factor \( \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}\) is often denoted by the symbol \( k\), and indeed that was the symbol \( I\) used in Section 15.3 (see Equation 15.3.3).
Expand Equation \( \ref{15.18.9}\) by the binomial theorem as far as \( (\frac{v}{c})^{2}\) and compare the result with Equations \( \ref{15.18.1}\) and \( \ref{15.18.2}\).
I make it
\[ \nu = \nu_{0}(1+(\frac{v}{c})+\frac{1}{2}(\frac{v}{c})^{2}...). \label{15.18.10} \]
An observer \( O\) sends an electromagnetic signal of frequency \( \nu_{0}\) at speed \( c\) to a mirror that is receding at speed \( v\). When the reflected signal arrives back at the observer, what is its frequency (to first order in \( \frac{v}{c}\))? Is it \( \nu_{0}(1-\frac{v}{c})\) or is it \( \nu_{0}(1-\frac{2v}{c})\)?
I can think offhand of two applications of this. If you examine the solar Fraunhofer spectrum reflected of the equatorial limb of a rotating planet, and you observe the fractional change \( \frac{\Delta\nu}{\nu_{0}}\) in the frequency of a spectrum line, will this tell you \( \frac{v}{c}\) or \( \frac{2v}{c}\), where \( v\) is the equatorial speed of the planet’s surface? And if a policeman directs a radar beam at your car, does the frequency of the returning beam tell him the speed of your car, or twice its speed? You could try arguing this case in court – or, better, stick to the speed limit so there is no need to do so. The answer, by the way, is \( \nu_{0}(1-\frac{2v}{c})\).
Redshift. When a galaxy is moving away from us, a spectrum line of laboratory wavelength \( \lambda_{0}\) will appear to have a frequency for the observer of \( \lambda=k\lambda_{0}\). The fractional increase in wavelength \( \frac{\lambda-\lambda_{0}}{\lambda_{0}}\) is generally given the symbol \( z\), which is evidently equal to \( k-1\). (Only to first order in \( \beta\) is it approximately equal to \( \beta\). It is important to note that the definition of \( z\) is \( \frac{\lambda-\lambda_{0}}{\lambda_{0}}\), and not \( \frac{v}{c}\).
A note on terminology: If a source is receding from the observer the light is observed to be shifted towards longer wavelengths, and if it is approaching the observer the light is shifted towards shorter wavelengths. Traditionally a shift to longer wavelengths is called a “redshift”, and a shift towards shorter wavelengths is called a “blueshift”. Note, however, that if an infrared source is approaching an observer, its light is shifted towards the red, and if an ultraviolet source is receding from an observer, its light is shifted towards the blue! Nevertheless, I shall continue in this chapter to refer to shifts to longer and shorter wavelengths as redshifts and blueshifts respectively.
A red galaxy R of wavelength 680.0 nm and a green galaxy G of wavelength 520.0 nm are on opposite sides of an observer X, both receding from him/her. To the observer, the wavelength of the red galaxy appears to be 820.0 nm, and the wavelength of the green galaxy appears to be 640.0 nm. What is the wavelength of the green galaxy as seen from the red galaxy?
Solution
We are told that \( k\) for the red galaxy is 82/68 = 1.20588, or \( z\) = 0.20588, and that \( k\) for the green galaxy \( k\) is 64/52 = 1.23077, or \( z\) = 0.23077. Because of the preparation we did in Section 15.3, we can instantly convert these to \( \phi\). Thus for the red galaxy \( \phi\)= 0.187212 and for the green galaxy \( \phi\) = 0.207639. The sum of these is 0.394851. We can instantly convert this to \( k = 1.48416\) or \( z = 0.48416.\). Thus, as seen from R, the wavelength of G is 771.8 nm.
Alternatively.
Show that the factor k combines as
\[ k_{1} \oplus k_{2} =k_{1}k_{2} \label{15.18.11} \]
and verify that \( \frac{82}{68}\times\frac{64}{52}=1.48416\). Show also that the redshift factor \( z\) combines as
\[ z_{1} \oplus z_{2} =z_{1}z_{2}+z_{1}+z_{2}. \label{15.18.12} \]


