2.10: Pendulums
- Page ID
- 8360
In Section 2.2, we discussed the physical meaning of the rotational inertia as being the ratio of the applied torque to the resulting angular acceleration. In linear motion, we are familiar with the equation \( F = ma\). The corresponding Equation when dealing with torques and angular acceleration is \( \tau = I\ddot{\theta}\). We are also familiar with the equation of motion for a mass vibrating at the end of a spring of force constant k : \( m\ddot{x} = -kx \). This is simple harmonic motion of period \( 2\pi\sqrt{\frac{m}{k}} \). The mechanics of the torsion pendulum is similar.
The torsion constant \( c \) of a wire is the torque required to twist it through unit angle. If a mass is suspended from a torsion wire, and the wire is twisted through an angle \( \theta \), the restoring torque will be \( c\theta \), and the Equation of motion is \( I\ddot{\theta} = -c\theta\), which is simple harmonic motion of period \( 2\pi\sqrt{\frac{I}{c}} \). The torsion constant of a wire of circular cross-section, by the way, is proportional to its shear modulus, the fourth power of its radius, and inversely as its length. The derivation of this takes a little trouble, but it can be verified by dimensional analysis. Thus a thick wire is very much harder to twist than a thin one. A wire of narrow rectangular cross-section, such as a strip or a ribbon has a relatively small torsion constant.
Now let's look not at a torsion pendulum, but at a pendulum swinging about an axis under gravity.
We suppose the pendulum, of mass \( m\), is swinging about a point O, which is at a distance \( h\) from the center of mass C. The rotational inertia about O is \( I\). The line OC makes an angle \( \theta\) with the vertical, so that the horizontal distance between O and C is \( h \sin\theta\). The torque about O is \(mgh \sin\theta\), so that the equation of motion is
\[ I \ddot{\theta} = -mgh\sin\theta. \tag{2.10.1}\label{eq:2.10.1} \]
For small angles (\(\sin \theta \approx \theta\)), this is
\[ I \ddot{\theta} = -mgh\theta. \tag{2.10.2}\label{eq:2.10.2} \]
This is simple harmonic motion of period
\[ P = 2 \pi \sqrt{\frac{I}{mgh}}. \tag{2.10.3}\label{eq:2.10.3} \]
We'll look at two examples - a uniform rod, and an arc of a circle.
First, a uniform rod.
The center of mass is C. The rotational inertia about C is \( \frac{1}{3}ml^{2}\), so the rotational inertia about O is \( I = \frac{1}{3}ml^{2} +mh^{2}\). If we substitute this in equation \( \ref{eq:2.10.3}\), we find for the period of small oscillations
\[ P = 2\pi\sqrt{\frac{l^{2}+3h^{2}}{3gh}}. \tag{2.10.4}\label{eq:2.10.4} \]
This can be written
\[ P = 2\pi\sqrt{\frac{l}{3g}}\cdot\sqrt{\frac{l+3(\frac{h}{l})^{2}}{\frac{h}{l}}}. \tag{2.10.5}\label{eq:2.10.5} \]
or, if we write \( \mathsf{P} = \frac{P}{2\pi\sqrt{\frac{l}{3g}}} \) and \( \mathsf{h} = \frac{h}{l}\):
\[ P = \sqrt{\frac{1+3 \mathsf{h}^{2}}{\mathsf{h}}}. \tag{2.10.6}\label{eq:2.10.6} \]
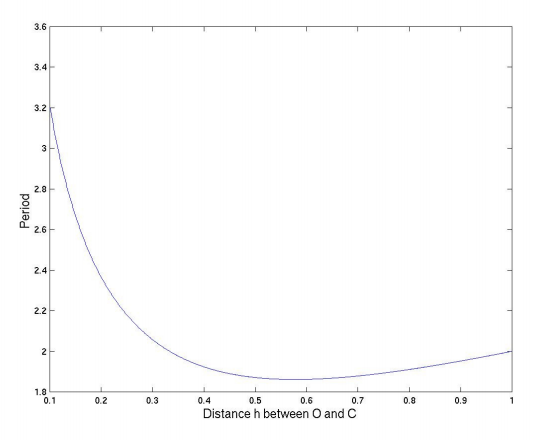
The figure shows a graph of \( \mathsf{P}\) versus \( \mathsf{h}\).
Equation \( \ref{eq:2.10.6}\) can be written
\[ \mathsf{P}^{2} = \frac{1}{ \mathsf{h}} + 3 \mathsf{h}. \tag{2.10.7}\label{eq:2.10.7} \]
and, by differentiation of \( \mathsf{P}^{2}\) with respect to \( \mathsf{h}\), we find that the period is least when \( \mathsf{h} = \frac{1}{\sqrt{3}}\).
This least period is given by \( \mathsf{P}^{2} = \sqrt{12}\),or \( \mathsf{P} = 1.861\).
Equation \( \ref{eq:2.10.7}\) can also be written
\[ \ 3 \mathsf{h}^{2} - \mathsf{P}^{2} \mathsf{h} + 1 = 0 \tag{2.10.8}\label{eq:2.10.8} \]
This quadratic Equation shows that there are two positions of the support \( O\) that give rise to the same period of small oscillations. The period is least when the two solutions of Equation \( \ref{eq:2.10.8}\) are equal, and by the theory of quadratic Equations, then, the least period is given by \( \mathsf{P}^{2} = \sqrt{12}\) as we also deduced by differentiation of Equation \( \ref{eq:2.10.7}\), and this occurs when\( \mathsf{h} = \frac{1}{\sqrt{3}}\).
For periods longer than this, there are two solutions for \( \mathsf{h}\). Let \( \mathsf{h}_{1}\) be the smaller of these, and let \( \mathsf{h}_{2}\) be the larger. By the theory of quadratic Equations, we have
\[ \ \mathsf{h}_{1} + \mathsf{h}_{2} = \frac{1}{3}\mathsf{P}^{2}\tag{2.10.9}\label{eq:2.10.9} \]
and
\[ \ \mathsf{h}_{1}\mathsf{h}_{2} = \frac{1}{3}\tag{2.10.10}\label{eq:2.10.10} \]
Let \( \mathsf{H} = \mathsf{h}_{2} - \mathsf{h}_{1}\) be the distance between two points \( O\) that give the same period of oscillation.
Then
\[ \ \mathsf{H}^{2} = (\mathsf{h}_{2} - \mathsf{h}_{1})^{2} = (\mathsf{h}_{2} + \mathsf{h}_{1})^{2} - 4\mathsf{h}_{1}\mathsf{h}_{2} = \frac{\mathsf{P}^{4}-12}{9}\tag{2.10.11}\label{eq:2.10.11} \]
If we measure \( \mathsf{H}\) for a given period \( \mathsf{P}\) and recall the definition of \( \mathsf{P}\) we see that this provides a method for determining \( g\). Although this is a common undergraduate laboratory exercise, the graph shows that the minimum is very shallow and consequently \( \mathsf{H}\) and hence \( g\) are very difficult to measure with any precision.
For another example, let us look at a wire bent into the arc of a circle of radius \( a\) oscillating in a vertical plane about its mid-point. In the figure, \( C\) is the center of mass.
The rotational inertia about the centerof the circle is \( ma^{2}\). By two applications of the parallel axes theorem, we see that the rotational inertia about the point of oscillation is \( I = ma^{2} - m(a-h)^{2} + mh^{2} = 2mah\).Thus, from Equation \( \ref{eq:2.10.3}\) we find
\[ P = 2\pi\sqrt{\frac{2a}{g}}, \tag{2.10.12}\label{eq:2.10.12} \]
and the period is independent of the length of the arc.


