2.20: Ellipses and Ellipsoids
- Page ID
- 8370
Here are some problems concerning ellipses and ellipsoids that might be of interest.
Determine the principal moments of inertia of the following:
- A uniform plane lamina of mass \(m\) in the form of an ellipse of semi axes \(a \) and \( b\).
- A uniform plane ring of mass \(m\) in the form of an ellipse of semi axes \(a \) and \( b\).
- A uniform solid triaxial ellipsoid of mass \(m\) and semi axes \(a, b \) and \( c\).
- A uniform hollow triaxial ellipsoid of mass \(m\) and semi axes \(a, b \) and \( c\).
1. By integration, an elliptical lamina is slightly difficult, but by physical insight it is very easy!
The distribution of mass around the minor axis is the same as for a circular lamina of radius \( a\), and therefore the moment \( B \) is the same as for the circular lamina, namely \( B = \frac{1}{4} ma^2 \). Similarly, \( A = \frac{1}{4} mb^2 \), and hence, by the perpendicular axes theorem, \(C = \frac{1}{4} m(a^2 + b^2 ) \).
I think you will find that the shape of the momental ellipse is the same as the shape of the original elliptical lamina.
2. An elliptical ring (hoop) is remarkably difficult. It cannot be expressed in terms of elementary functions, and it has to be calculated numerically. It can be expressed in terms of elliptic integrals (no surprise there), but most of us aren’t sure what elliptic integrals are and they hardly count as elementary functions, and they have to be calculated numerically anyway. We take the ellipse to be \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \) with \( b≤a \).
Even calculating the circumference of an ellipse isn’t all that easy. The circumference is
\( \oint ds = 4 \int_{0}^{a} [ 1 + (\frac{dy}{dx} )^2] dx \), with \( y = b ( 1 - \frac{x^2}{a^2} )^\frac{1}{2} \).
After a bit of algebra, this can be written as
\( \frac{4a}{x} \int_{0}^{a} \sqrt{\frac{c^2 -x^2}{a^2 - z^2}}dx \), where \( c^2 = \frac{a^4}{a^2 - b^2} \).
At first this looks easy, but I do not think you can do it in terms of elementary functions. No problem, then – just integrate it numerically. Unfortunately the integrand becomes infinite at the upper limit, so there is still a bit of a problem. However, a change of variable to \( x = a \sin \theta \) solves that problem. The expression for the circumference becomes simply
\( 4a\int_{0}^{\pi /2 } [1 - (\frac{a^2 - b^2}{a^2}) \sin ^2 \theta ]^\frac{1}{2} d \theta \),
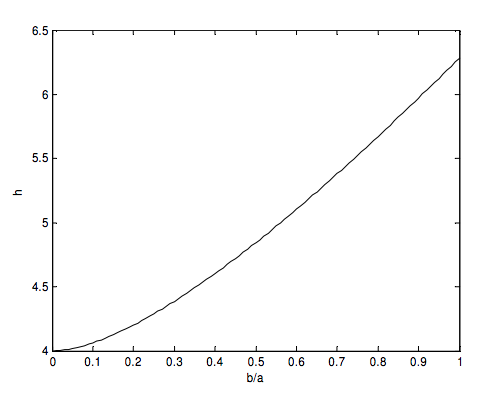
which can be integrated numerically without infinity problems at the limits. According to my calculations, the circumference of the ellipse is \( ha \), where \(h\) is a function of \(b/a \) as follows:
To find the moment of inertia (or the second moment of length) about the minor axis, we have to multiple the integrand by \(x^2 \), or \( a^2 \sin^2 \theta \), and integrate. Thus the moment of inertia of the elliptical hoop about its minor axis is \(c_1ma^2 \), where
\( c_1 = \frac{\int_{0}^{\pi / 2 } [1 - ( \frac{a^2 - b^2}{a^2} ) \sin^2 \theta ] ^{1/2} \sin^2
\theta d \theta }{ \int_{0}^{\pi / 2 } [ 1- (\frac{a^2 - b^2}{a^2} )\sin^2 \theta ]^{1/2} d \theta} \)
The moment of inertia about the major axis is \(c_2ma^2 \), where
\( c_2 = \frac{ \frac{b^2}{a^2}\int_{0}^{\pi / 2 } [1 - ( \frac{a^2 - b^2}{a^2} ) cos^2]^{1/2} \sin^2 \theta d \theta }{ \int_{0}^{\pi / 2 } [ 1- (\frac{a^2 - b^2}{a^2} )\sin^2 \theta ]^{1/2} d \theta} \)
These two coefficients of \(ma^2 \) are shown below as a function of \(b/a \).
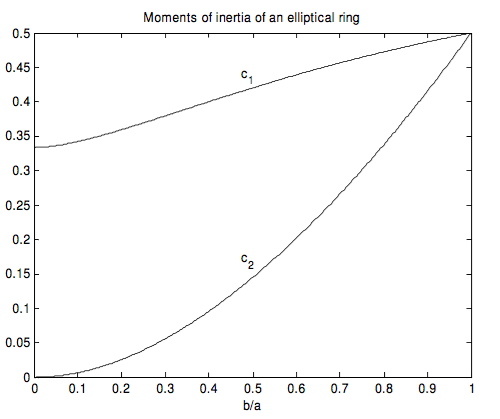
The moments of inertia of an elliptical ring of mass \(m\) and semi major and semi minor axes \(a\) and \(b\) are \(c_1ma^2 \) about the minor axis and \( c_2ma^2 \) about the major axis, where \(c_1 \) and \(c_2 \) are shown as functions of \(b/a \).
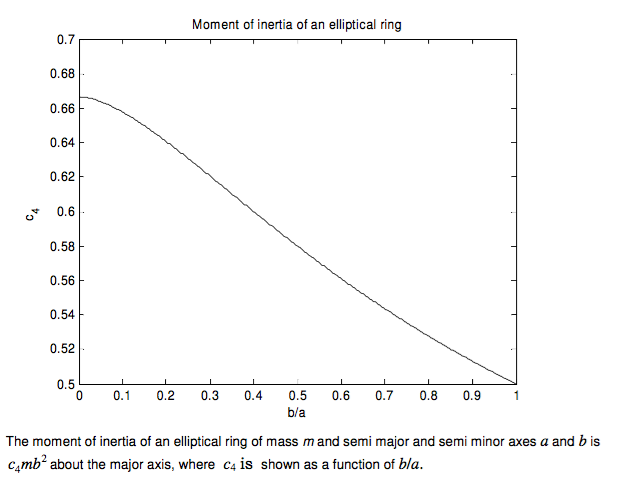
The moment of inertia about the major axis can also be conveniently expressed in terms of \( b \) rather than \(a \). If we write the moment of inertia about the major axis as \(c_4mb^2\), then \(c_4 \) as a function of \(b/a \) is shown below.
The moment of inertia about an axis perpendicular to the plane of the ellipse and passing through its centre is \(c_3ma^2 \), where, of course (by the perpendicular axes theorem), \( c_3 = c_1 + c_2 \).
It is also equal to \( c_1ma^2 + c_4mb^2 \).
3. For a uniform solid triaxial ellipsoid, the moments of inertia are
\( A = \frac{1}{5} m(b^2 + c^2) \qquad B = \frac{1}{5} m(c^2 + a^2) \qquad C = \frac{1}{5} m(c^2 + a^2) \)
The momental ellipsoid is not of the same shape. Its axes are in the ratio
\( \)
For example, if the axial ratios of the original ellipsoid are 1 : 2 : 3, the axial ratios of the corresponding momental ellipsoid is \( 1 : \sqrt{\frac{13}{10}} : \sqrt{\frac{13}{5}} = 1 : 1.140 : 1.612 \), which is slightly more spherical than the original ellipsoid.
4. Triaxial elliptical shell. We have to think carefully about what a triaxial elliptical shell is. If we imagine the inner surface of the shell to be an ellipsoid, and the outer surface to be a similar ellipsoid, but with all linear dimensions increased by the same small fractional increment, then we obtain a figure like this:
In this drawing the linear size of the outer surface is 3 percent larger than that of the inner surface. E. J. Routh correctly shows in his treatise on rigid bodies that the principal moments of inertia of such a figure are \( \frac{1}{3} m(b^2 + c^2), \frac{1}{3} m(c^2 + a^2), \frac{1}{3}m(a^2 + b^2) \).
But it can be seen that such a figure is not (as presumably a rugger ball is) of uniform thickness. I draw below a shell of uniform thickness. In such a case the inner and outer surfaces are not exactly similar.
In attempting to calculate the moment of inertia of such a figure I shall restrict myself to the case of a spheroidal shell of uniform thickness. That is to say, an ellipsoid with two equal axes, represented by the equation, in cylindrical coordinates
\( \frac{\rho^2}{a^2} + \frac{z^2}{c^2} = 1, \)
where \( \rho^2 = x^2 + y^2 \). Further, if I put \( c = \chi a \), the equation to the spheroid can be written
\( \rho^2 + \frac{z^2}{\chi^2} = a^2, \)
If \( \chi < 1 \), the spheroid is oblate. If \( \chi > 1 \), the spheroid is prolate.
We’ll first need to calculate its surface area, which is
\( A = 4 \pi \int_{0}^{c} \rho [ 1 + (\frac{d\rho}{dz})^2]^\frac{1}{2} dz \)
After some algebra, this comes to
\( A = 4 \pi a^2 f (\chi ), \)
where
\( f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{1 - \chi^2}} \ln \left( \dfrac{1 + \sqrt{1 - \chi^2}}{\chi}\right)+1\right] \) for \( \chi \leq 1 \)
and
\( f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{\chi^2-1}} \sin^{-1}\left( \dfrac{\sqrt{\chi^2-1}}{\chi}\right)+1\right]] \) for \( \chi \geq 1 \)
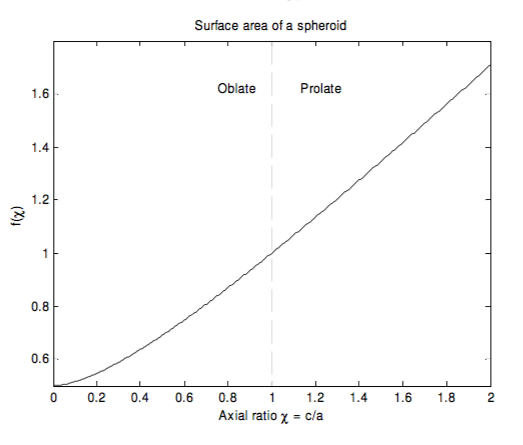
This function is shown below as far as \( \chi = 2 \). For \( \chi = 0 \), the figure is a disc whose total area
(upper and lower surface) is \(2 \pi a^2 \), and \( f = \frac{1}{2} \). For \( \chi = 1 \), the figure is a sphere whose area is \( 4 \pi a^2 \), and \( f = 1 \). The function goes to infinity as \( \chi \) goes to infinity.
The moment of inertia about the \(z\)-axis is
\( I = \frac{4 \pi m }{A}\int_{0}^{c} \rho ^3 [ 1 +(\frac{d \rho}{dz})^2]^{1/2} dz. \)
After some algebra this becomes
\( I = ma^2 g ( \chi ) \)
\( g ( \chi ) = \frac{(2-\chi ^2) (1-\chi ^2) - \chi^4 \ln\left[\left(1 + \sqrt{1- \chi^2}\right)/ \chi\right]}{4 \left\{ (1- \chi^2)^{3/2} + \chi^2 (1-\chi^2) \ln\left[(1 + \sqrt{1- \chi^2})/ \chi \right]\right\} } \) for \( \chi \leq 1 \)
\( g (\chi) = 1 - \frac{\frac{\chi^4}{(\chi - 1)^{3/2}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right)+\frac{\chi^2 -2}{\chi^2 -1 }}{4 \left\{ \frac{\chi^2}{\sqrt{\chi^2-1}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right) +1 \right\}} \) for \( \chi \geq 1 \)
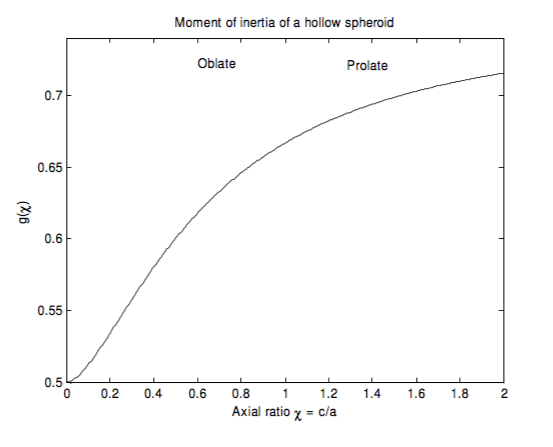
This function is shown below as far as \( \chi = 2 \) For \( \chi = 0 \), the figure is a disc whose moment of inertia is \( \frac{1}{2} \pi a^2 \), and \(f = \frac{1}{2} \). For \( \chi = 1 \), the figure is a hollow sphere whose moment of inertia is \( \frac{2}{3} \pi a^2 \), and \( f = \frac{2}{3} \). The function goes to 1 as \( \chi\) goes to infinity; the moment of inertia then approaches that of a hollow cylinder.