4.3: Kinetic Energy of Rigid Body Rotation
- Page ID
- 6948
Most of us are familiar with the formula \(\dfrac{1}{2} I \boldsymbol\omega^{2}\) for the rotational kinetic energy of a rotating solid body. This formula is adequate for simple situations in which a body is rotating about a principal axis, but is not adequate for a body rotating about a non-principal axis.
I am going to think of a rotating solid body as a collection of point masses, fixed relative to each other, but all revolving with the same angular velocity about a common axis – and those who believe in atoms assure me that this is indeed the case. (If you believe that a solid is a continuum, you can still divide it in your imagination into lots of small mass elements.)
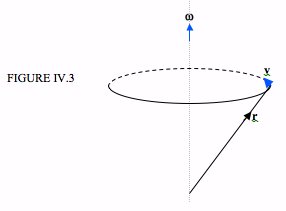
In Figure IV.3, I show just one particle of the rotating body. The position vector of the particle is {\bf r}. The body is rotating at angular velocity \( \boldsymbol\omega\). I hope you’ll agree that the linear velocity {\bf v} of the particle is (now think about this carefully) \( v = \boldsymbol \omega \times \bf{r} \).
The rotational kinetic energy of the solid body is
\[{\bf T}_{rot} = \dfrac{1}{2} \sum {\bf m} \nu^{2} = \sum {\bf v} \cdot {\bf mv} =\dfrac{1}{2} \sum (\boldsymbol\omega \times {\bf r})\cdot {\bf p} \nonumber \]
The triple scalar product is the volume of a parallelepiped, which justifies the next step:
\[T_{rot}=\dfrac{1}{2} \sum \boldsymbol\omega \cdot (r\times p) \nonumber \]
All particles have the same angular velocity, so:
\[ T_{rot}=\dfrac{1}{2} \boldsymbol\omega \cdot \sum ({\bf r}\times {\bf p}) = \dfrac{1}{2} \boldsymbol\omega \cdot {\bf L}= \dfrac{1}{2} \boldsymbol\omega \cdot {\bf l} \boldsymbol\omega \nonumber \]
Thus we arrive at the following expressions for the rotational kinetic energy:
\[ \ T_{rot} = \dfrac{1}{2} \boldsymbol\omega {\bf L}= \dfrac{1}{2} \boldsymbol\omega \bf{I} \boldsymbol\omega\tag{4.3.1}\label{eq:4.3.1} \]
If the body is rotating about a nonprincipal axis, the vectors \(\boldsymbol\omega\) and \( \bf{L}\) are not parallel (we shall discuss this in more detail in later sections). If it is rotating about a principal axis, they are parallel, and the expression reduces to the familiar \(\dfrac{1}{2} I \omega^{2}\)
In matrix notation, this can be written
\[ \ T_{rot} = \dfrac{1}{2} \widetilde{\boldsymbol\omega} \bf{I} \omega\tag{4.3.2}\label{eq:4.3.2} \]
Here \( \bf{I}\) is the inertia tensor, \(\omega\) is a column vector containing the rectangular components of the angular velocity and \( \widetilde{\boldsymbol\omega} \) is its transpose, namely a row vector.
That is:
\[ \begin{align} T_{rot} & = (\omega_{x} \omega_{y} \omega_{z})\left(\begin{array}{c}A & -H &-G \\-H & B & -F \\ -G & -F & C\end{array}\right)\left(\begin{array}{c}\omega_{x}\\ \omega_{y} \\\omega_{z}\end{array}\right) \tag{4.3.3} \label{eq:4.3.3} \\ & = \dfrac{1}{2}(A\omega^{2}_{x}+B\omega^{2}_{y}+C\omega^{2}_{z}-2F\omega_{y}\omega_{z}-2G\omega_{z}\omega_{x} - 2H\omega_{x}\omega_{y} \end{align} \tag{4.3.4}\label{eq:4.3.4} \]
This expression gives the rotational kinetic energy when the components of the inertia tensor and the angular velocity vector are referred to an arbitrary set of axes. If we refer them to the principal axes, the off-diagonal elements are zero. I am going to call the principal moments of inertia \( I_{1}\), \( I_{2}\) and \( I_{3}\). (I could call them \( A\), \( B\) and \( C\), but I shall often use the convention that \( A<B<C\), and I do not want to specify at the present which of the three moments is the greatest and which is the greatest, so I’ll call them \( I_{1}\), \( I_{2}\) and \( I_{3}\), with \( I_{1}\) = \(\sum m(y^{2} + z^{2}\), etc.). I’ll also call the angular velocity components referred to the principal axes \( \omega_{1}\), \( \omega_{2}\) , \( \omega_{3}\). Referred, then, to the principal axes, the rotational kinetic energy is
\[ \ T = \dfrac{1}{2}(I_{1} \omega_{1}^{2} +I_{2} \omega_{2}^{2} +I_{3} \omega_{3}^{2} ). \tag{4.3.5}\label{eq:4.3.5} \]
I have now dropped the subscript “rot”, because in this chapter I am dealing entirely with rotational motion, and so \( T\) can safely be understood to mean rotational kinetic energy.
We can also now write the kinetic energy in terms of the rates of change of the Eulerian angles, and the expression we obtain will be useful later when we derive Euler’s equations of motion:
\[ T = \dfrac{1}{2}I_{1} (\dot{\phi}\sin\psi + \dot{\theta}\cos \psi)^{2} + \dfrac{1}{2}I_{2} (\dot{\phi}\sin\theta cos\psi - \dot{\theta}\sin \psi)^{2} + I_{1} (\dot{\phi} \cos \theta + \dot{\psi})^{2} \tag{4.3.6}\label{eq:4.3.6} \]
You will probably want a concrete example in order to understand this properly,
Let us imagine that we have a concrete brick of dimensions 10 cm x 15 cm x 20 cm, and of density 4 g cm-3 , and that it is rotating about a body diameter (the ends of which are fixed) at an angular speed of 6 rad s-1 .
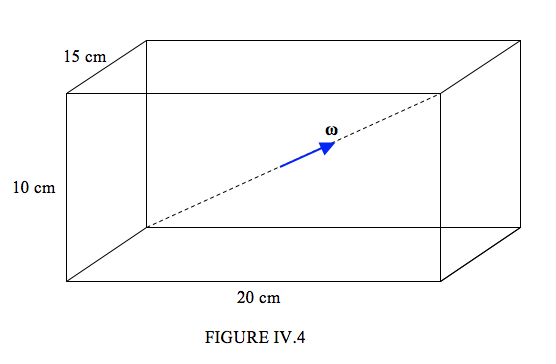
I hope you’ll agree that the mass is 12000 g = 12 kg.
The principal moment of inertia about the vertical axis is
\( I_{3} = \dfrac{1}{3} \times 12000 \times (10^{2} + 7.5^{2})\) = 625,000 g cm2 = 0.0625 kg m2.
Similarly the other principal moments are
\( I_{1}\) = 0.0500 kg m2 and \( I_{2}\) = 0.0325 kg m2 .
The direction cosines of the vector \(\omega\) are
\[\dfrac{15}{\sqrt{15^{2} + 20^{2} +10^{2}}} , \dfrac{20}{\sqrt{15^{2} + 20^{2} +10^{2}}}, \dfrac{10}{\sqrt{15^{2} + 20^{2} +10^{2}}} \nonumber \]
Therefore \(\omega_{1}\) = 3.34252 rad s-1, \(\omega_{2}\) = 4.45669 rad s-1, \(\omega_{3}\) = 2.22834 rad s-1 .
Hence T = 0.02103 J


