26.2: Vision Correction
- Page ID
- 2734
Learning Objectives
By the end of this section, you will be able to:
- Identify and discuss common vision defects.
- Explain nearsightedness and farsightedness corrections.
- Explain laser vision correction.
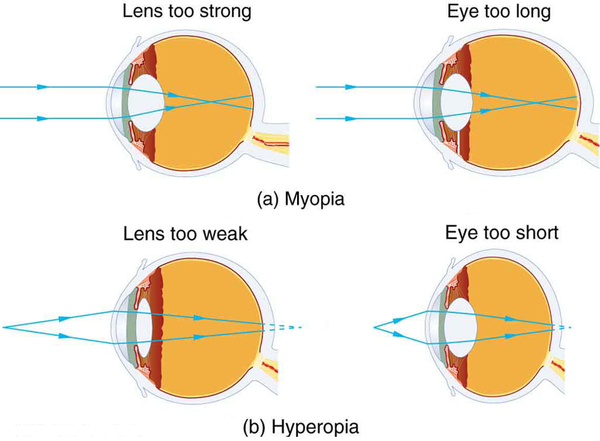
The need for some type of vision correction is very common. Common vision defects are easy to understand, and some are simple to correct. Figure \(\PageIndex{1}\) illustrates two common vision defects. Nearsightedness, or myopia, is the inability to see distant objects clearly while close objects are clear. The eye overconverges the nearly parallel rays from a distant object, and the rays cross in front of the retina. More divergent rays from a close object are converged on the retina for a clear image. The distance to the farthest object that can be seen clearly is called the far point of the eye (normally infinity). Farsightedness, or hyperopia, is the inability to see close objects clearly while distant objects may be clear. A farsighted eye does not converge sufficient rays from a close object to make the rays meet on the retina. Less diverging rays from a distant object can be converged for a clear image. The distance to the closest object that can be seen clearly is called the near point of the eye (normally 25 cm).
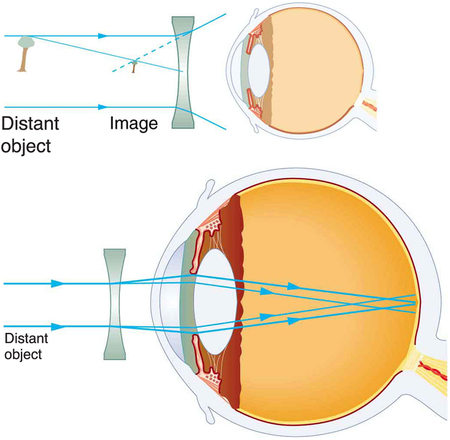
Since the nearsighted eye over converges light rays, the correction for nearsightedness is to place a diverging spectacle lens in front of the eye. This reduces the power of an eye that is too powerful. Another way of thinking about this is that a diverging spectacle lens produces a case 3 image, which is closer to the eye than the object (Figure \(\PageIndex{2}\)). To determine the spectacle power needed for correction, you must know the person’s far point -- that is, you must know the greatest distance at which the person can see clearly. Then the image produced by a spectacle lens must be at this distance or closer for the nearsighted person to be able to see it clearly. It is worth noting that wearing glasses does not change the eye in any way. The eyeglass lens is simply used to create an image of the object at a distance where the nearsighted person can see it clearly. Whereas someone not wearing glasses can see clearly objects that fall between their near point and their far point, someone wearing glasses can see images that fall between their near point and their far point.
Example \(\PageIndex{1}\): Correcting Nearsightedness
What power of spectacle lens is needed to correct the vision of a nearsighted person whose far point is 30.0 cm? Assume the spectacle (corrective) lens is held 1.50 cm away from the eye by eyeglass frames.
Strategy:
You want this nearsighted person to be able to see very distant objects clearly. That means the spectacle lens must produce an image 30.0 cm from the eye for an object very far away. An image 30.0 cm from the eye will be 28.5 cm to the left of the spectacle lens (Figure \(\PageIndex{2}\)). Therefore, we must get \(d_{i} = -28.5 cm\) when \(d_{o} \approx \infty \). The image distance is negative, because it is on the same side of the spectacle as the object.
Solution
Since \(d_{i}\) and \(d_{o}\) are known, the power of the spectacle lens can be found using \(P = \frac{1}{d_{o}} + \frac{1}{d_{i}}\) as written earlier:
\[P = \frac{1}{d_{o}} + \frac{1}{d_{i}} = \frac{1}{\infty} + \frac{1}{-0.285 m}.\]
Since \(1/ \infty = 0\), we obtain: \[P = 0 - 3.51/m = -3.51 D.\]
Discussion:
The negative power indicates a diverging (or concave) lens, as expected. The spectacle produces a case 3 image closer to the eye, where the person can see it. If you examine eyeglasses for nearsighted people, you will find the lenses are thinnest in the center. Additionally, if you examine a prescription for eyeglasses for nearsighted people, you will find that the prescribed power is negative and given in units of diopters.
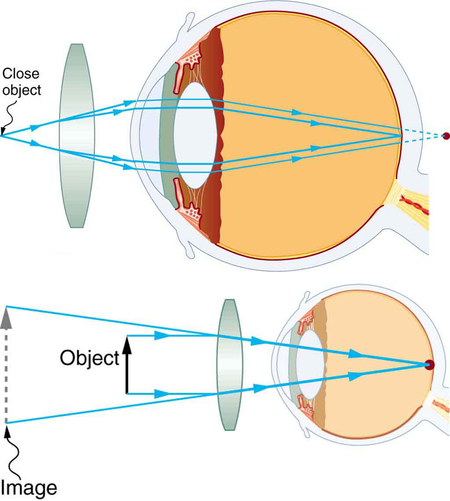
Since the farsighted eye under converges light rays, the correction for farsightedness is to place a converging spectacle lens in front of the eye. This increases the power of an eye that is too weak. Another way of thinking about this is that a converging spectacle lens produces a case 2 image, which is farther from the eye than the object (Figure \(\PageIndex{3}\)). To determine the spectacle power needed for correction, you must know the person’s near point -- that is, you must know the smallest distance at which the person can see clearly. Then the image produced by a spectacle lens must be at this distance or farther for the farsighted person to be able to see it clearly.
Example \(\PageIndex{2}\):Correcting Farsightedness
What power of spectacle lens is needed to allow a farsighted person, whose near point is 1.00 m, to see an object clearly that is 25.0 cm away? Assume the spectacle (corrective) lens is held 1.50 cm away from the eye by eyeglass frames.
Strategy
When an object is held 25.0 cm from the person’s eyes, the spectacle lens must produce an image 1.00 m away (the near point). An image 1.00 m from the eye will be 98.5 cm to the left of the spectacle lens because the spectacle lens is 1.50 cm from the eye (Figure \(\PageIndex{3}\)). Therefore, \(d_{i} = -98.5 cm\). The image distance is negative, because it is on the same side of the spectacle as the object. The object is 23.5 cm to the left of the spectacle, so that \(d_{o} = 23.5 cm\).
Solution
Since \(d_{i}\) and \(d_{o}\) are known, the power of the spectacle lens can be found using \(P = \frac{1}{d_{o}} + \frac{1}{d_{i}}\): \[P = \frac{1}{d_{o}} + \frac{1}{d_{i}} = \frac{1}{0.235 m} + \frac{1}{-0.985 m}\] \[4.26D - 1.02D = 3.24D.\]
Discussion
The positive power indicates a converging (convex) lens, as expected. The convex spectacle produces a case 2 image farther from the eye, where the person can see it. If you examine eyeglasses of farsighted people, you will find the lenses to be thickest in the center. In addition, a prescription of eyeglasses for farsighted people has a prescribed power that is positive.
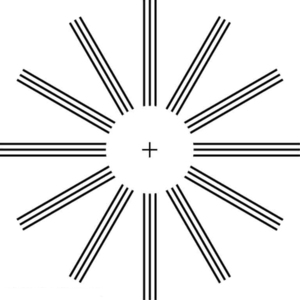
Another common vision defect is astigmatism an unevenness or asymmetry in the focus of the eye. For example, rays passing through a vertical region of the eye may focus closer than rays passing through a horizontal region, resulting in the image appearing elongated. This is mostly due to irregularities in the shape of the cornea but can also be due to lens irregularities or unevenness in the retina. Because of these irregularities, different parts of the lens system produce images at different locations. The eye-brain system can compensate for some of these irregularities, but they generally manifest themselves as less distinct vision or sharper images along certain axes. Figure \(\PageIndex{4}\) shows a chart used to detect astigmatism. Astigmatism can be at least partially corrected with a spectacle having the opposite irregularity of the eye. If an eyeglass prescription has a cylindrical correction, it is there to correct astigmatism. The normal corrections for short- or farsightedness are spherical corrections, uniform along all axes.
Contact lenses have advantages over glasses beyond their cosmetic aspects. One problem with glasses is that as the eye moves, it is not at a fixed distance from the spectacle lens. Contacts rest on and move with the eye, eliminating this problem. Because contacts cover a significant portion of the cornea, they provide superior peripheral vision compared with eyeglasses. Contacts also correct some corneal astigmatism caused by surface irregularities. The tear layer between the smooth contact and the cornea fills in the irregularities. Since the index of refraction of the tear layer and the cornea are very similar, you now have a regular optical surface in place of an irregular one. If the curvature of a contact lens is not the same as the cornea (as may be necessary with some individuals to obtain a comfortable fit), the tear layer between the contact and cornea acts as a lens. If the tear layer is thinner in the center than at the edges, it has a negative power, for example. Skilled optometrists will adjust the power of the contact to compensate.
Laser vision correction has progressed rapidly in the last few years. It is the latest and by far the most successful in a series of procedures that correct vision by reshaping the cornea. As noted at the beginning of this section, the cornea accounts for about two-thirds of the power of the eye. Thus, small adjustments of its curvature have the same effect as putting a lens in front of the eye. To a reasonable approximation, the power of multiple lenses placed close together equals the sum of their powers. For example, a concave spectacle lens (for nearsightedness) having \(P = -3.00 D\) has the same effect on vision as reducing the power of the eye itself by 3.00 D. So to correct the eye for nearsightedness, the cornea is flattened to reduce its power. Similarly, to correct for farsightedness, the curvature of the cornea is enhanced to increase the power of the eye -- the same effect as the positive power spectacle lens used for farsightedness. Laser vision correction uses high intensity electromagnetic radiation to ablate (to remove material from the surface) and reshape the corneal surfaces.
Today, the most commonly used laser vision correction procedure is Laser in situ Keratomileusis (LASIK). The top layer of the cornea is surgically peeled back and the underlying tissue ablated by multiple bursts of finely controlled ultraviolet radiation produced by an excimer laser. Lasers are used because they not only produce well-focused intense light, but they also emit very pure wavelength electromagnetic radiation that can be controlled more accurately than mixed wavelength light. The 193 nm wavelength UV commonly used is extremely and strongly absorbed by corneal tissue, allowing precise evaporation of very thin layers. A computer controlled program applies more bursts, usually at a rate of 10 per second, to the areas that require deeper removal. Typically a spot less than 1 mm in diameter and about \(0.3 \mu m\) in thickness is removed by each burst. Nearsightedness, farsightedness, and astigmatism can be corrected with an accuracy that produces normal distant vision in more than 90% of the patients, in many cases right away. The corneal flap is replaced; healing takes place rapidly and is nearly painless. More than 1 million Americans per year undergo LASIK (Figure \(\PageIndex{5}\)).
Summary
- Nearsightedness, or myopia, is the inability to see distant objects and is corrected with a diverging lens to reduce power.
- Farsightedness, or hyperopia, is the inability to see close objects and is corrected with a converging lens to increase power.
- In myopia and hyperopia, the corrective lenses produce images at a distance that the person can see clearly—the far point and near point, respectively.
Glossary
- nearsightedness
- another term for myopia, a visual defect in which distant objects appear blurred because their images are focused in front of the retina rather than being focused on the retina
- myopia
- a visual defect in which distant objects appear blurred because their images are focused in front of the retina rather than being focused on the retina
- far point
- the object point imaged by the eye onto the retina in an unaccommodated eye
- farsightedness
- another term for hyperopia, the condition of an eye where incoming rays of light reach the retina before they converge into a focused image
- hyperopia
- the condition of an eye where incoming rays of light reach the retina before they converge into a focused image
- near point
- the point nearest the eye at which an object is accurately focused on the retina at full accommodation
- astigmatism
- the result of an inability of the cornea to properly focus an image onto the retina
- laser vision correction
- a medical procedure used to correct astigmatism and eyesight deficiencies such as myopia and hyperopia


