8.2: Distortion of Space and Time
- Page ID
- 959
7.2.1 The Lorentz transformation
Relativity says that when two observers are in different frames of reference, each observer considers the other one's perception of time to be distorted. We'll also see that something similar happens to their observations of distances, so both space and time are distorted. What exactly is this distortion? How do we even conceptualize it?
The idea isn't really as radical as it might seem at first. We can visualize the structure of space and time using a graph with position and time on its axes. These graphs are familiar by now, but we're going to look at them in a slightly different way. Before, we used them to describe the motion of objects. The grid underlying the graph was merely the stage on which the actors played their parts. Now the background comes to the foreground: it's time and space themselves that we're studying. We don't necessarily need to have a line or a curve drawn on top of the grid to represent a particular object. We may, for example, just want to talk about events, depicted as points on the graph as in figure a.
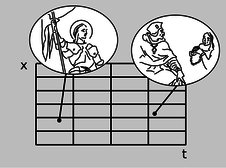
a / Two events are given as points on a graph of position versus time. Joan of Arc helps to restore Charles VII to the throne. At a later time and a different position, Joan of Arc is sentenced to death.
A distortion of the Cartesian grid underlying the graph can arise for perfectly ordinary reasons that Isaac Newton would have readily accepted. For example, we can simply change the units used to measure time and position, as in figure b.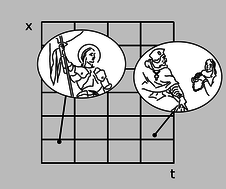
b / A change of units distorts an \(x\)-\(t\) graph. This graph depicts exactly the same events as figure a. The only change is that the \(x\) and \(t\) coordinates are measured using different units, so the grid is compressed in \(t\) and expanded in \(x\).
We're going to have quite a few examples of this type, so I'll adopt the convention shown in figure c for depicting them. Figure c summarizes the relationship between figures a and b in a more compact form. The gray rectangle represents the original coordinate grid of figure a, while the grid of black lines represents the new version from figure b. Omitting the grid from the gray rectangle makes the diagram easier to decode visually.

c / A convention we'll use to represent a distortion of time and space.
Our goal of unraveling the mysteries of special relativity amounts to nothing more than finding out how to draw a diagram like c in the case where the two different sets of coordinates represent measurements of time and space made by two different observers, each in motion relative to the other. Galileo and Newton thought they knew the answer to this question, but their answer turned out to be only approximately right. To avoid repeating the same mistakes, we need to clearly spell out what we think are the basic properties of time and space that will be a reliable foundation for our reasoning. I want to emphasize that there is no purely logical way of deciding on this list of properties. The ones I'll list are simply a summary of the patterns observed in the results from a large body of experiments. Furthermore, some of them are only approximate. For example, property 1 below is only a good approximation when the gravitational field is weak, so it is a property that applies to special relativity, not to general relativity.
Experiments show that:
- No point in time or space has properties that make it different from any other point.
- Likewise, all directions in space have the same properties.
- Motion is relative, i.e., all inertial frames of reference are equally valid.
- Causality holds, in the sense described on page 381.
- Time depends on the state of motion of the observer.
Most of these are not very subversive. Properties 1 and 2 date back to the time when Galileo and Newton started applying the same universal laws of motion to the solar system and to the earth; this contradicted Aristotle, who believed that, for example, a rock would naturally want to move in a certain special direction (down) in order to reach a certain special location (the earth's surface). Property 3 is the reason that Einstein called his theory “relativity,” but Galileo and Newton believed exactly the same thing to be true, as dramatized by Galileo's run-in with the Church over the question of whether the earth could really be in motion around the sun. Property 4 would probably surprise most people only because it asserts in such a weak and specialized way something that they feel deeply must be true. The only really strange item on the list is 5, but the Hafele-Keating experiment forces it upon us.
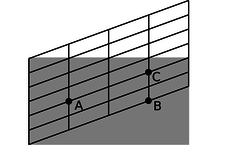
d / A Galilean version of the relationship between two frames of reference. As in all such graphs in this chapter, the original coordinates, represented by the gray rectangle, have a time axis that goes to the right, and a position axis that goes straight up.
If it were not for property 5, we could imagine that figure d would give the correct transformation between frames of reference in motion relative to one another. Let's say that observer 1, whose grid coincides with the gray rectangle, is a hitch-hiker standing by the side of a road. Event A is a raindrop hitting his head, and event B is another raindrop hitting his head. He says that A and B occur at the same location in space. Observer 2 is a motorist who drives by without stopping; to him, the passenger compartment of his car is at rest, while the asphalt slides by underneath. He says that A and B occur at different points in space, because during the time between the first raindrop and the second, the hitch-hiker has moved backward. On the other hand, observer 2 says that events A and C occur in the same place, while the hitch-hiker disagrees. The slope of the grid-lines is simply the velocity of the relative motion of each observer relative to the other.
Figure d has familiar, comforting, and eminently sensible behavior, but it also happens to be wrong, because it violates property 5. The distortion of the coordinate grid has only moved the vertical lines up and down, so both observers agree that events like B and C are simultaneous. If this was really the way things worked, then all observers could synchronize all their clocks with one another for once and for all, and the clocks would never get out of sync. This contradicts the results of the Hafele-Keating experiment, in which all three clocks were initially synchronized in Washington, but later went out of sync because of their different states of motion.
It might seem as though we still had a huge amount of wiggle room available for the correct form of the distortion. It turns out, however, that properties 1-5 are sufficient to prove that there is only one answer, which is the one found by Einstein in 1905. To see why this is, let's work by a process of elimination.
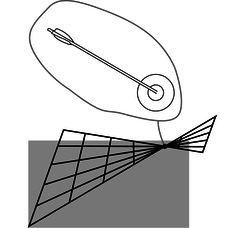
e / A transformation that leads to disagreements about whether two events occur at the same time and place. This is not just a matter of opinion. Either the arrow hit the bull's-eye or it didn't.
Figure e shows a transformation that might seem at first glance to be as good a candidate as any other, but it violates property 3, that motion is relative, for the following reason. In observer 2's frame of reference, some of the grid lines cross one another. This means that observers 1 and 2 disagree on whether or not certain events are the same. For instance, suppose that event A marks the arrival of an arrow at the bull's-eye of a target, and event B is the location and time when the bull's-eye is punctured. Events A and B occur at the same location and at the same time. If one observer says that A and B coincide, but another says that they don't, we have a direct contradiction. Since the two frames of reference in figure e give contradictory results, one of them is right and one is wrong. This violates property 3, because all inertial frames of reference are supposed to be equally valid. To avoid problems like this, we clearly need to make sure that none of the grid lines ever cross one another.
The next type of transformation we want to kill off is shown in figure f, in which the grid lines curve, but never cross one another. The trouble with this one is that it violates property 1, the uniformity of time and space. The transformation is unusually “twisty” at A, whereas at B it's much more smooth. This can't be correct, because the transformation is only supposed to depend on the relative state of motion of the two frames of reference, and that given information doesn't single out a special role for any particular point in spacetime. If, for example, we had one frame of reference rotating relative to the other, then there would be something special about the axis of rotation. But we're only talking about inertial frames of reference here, as specified in property 3, so we can't have rotation; each frame of reference has to be moving in a straight line at constant speed. For frames related in this way, there is nothing that could single out an event like A for special treatment compared to B, so transformation f violates property 1.
The examples in figures e and f show that the transformation we're looking for must be linear, meaning that it must transform lines into lines, and furthermore that it has to take parallel lines to parallel lines. Einstein wrote in his 1905 paper that “... on account of the property of homogeneity [property 1] which we ascribe to time and space, the [transformation] must be linear.”1 Applying this to our diagrams, the original gray rectangle, which is a special type of parallelogram containing right angles, must be transformed into another parallelogram. There are three types of transformations, figure g, that have this property. Case I is the Galilean transformation of figure d on page 386, which we've already ruled out.
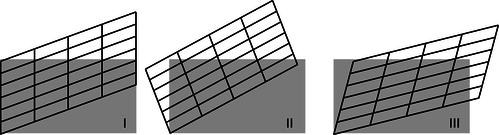
g / Three types of transformations that preserve parallelism. Their distinguishing feature is what they do to simultaneity, as shown by what happens to the left edge of the original rectangle. In I, the left edge remains vertical, so simultaneous events remain simultaneous. In II, the left edge turns counterclockwise. In III, it turns clockwise.
Case II can also be discarded. Here every point on the grid rotates counterclockwise. What physical parameter would determine the amount of rotation? The only thing that could be relevant would be \(v\), the relative velocity of the motion of the two frames of reference with respect to one another. But if the angle of rotation was proportional to \(v\), then for large enough velocities the grid would have left and right reversed, and this would violate property 4, causality: one observer would say that event A caused a later event B, but another observer would say that B came first and caused A.
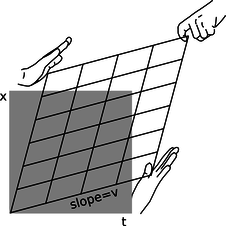
h / In the units that are most convenient for relativity, the transformation has symmetry about a 45-degree diagonal line.
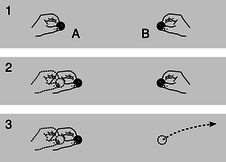
The only remaining possibility is case III, which I've redrawn in figure h with a couple of changes. This is the one that Einstein predicted in 1905. The transformation is known as the Lorentz transformation, after HendrikLorentz (1853-1928), who partially anticipated Einstein's work, without arriving at the correct interpretation. The distortion is a kind of smooshing and stretching, as suggested by the hands. Also, we've already seen in figures a-c on page 385 that we're free to stretch or compress everything as much as we like in the horizontal and vertical directions, because this simply corresponds to choosing different units of measurement for time and distance. In figure h I've chosen units that give the whole drawing a convenient symmetry about a 45-degree diagonal line. Ordinarily it wouldn't make sense to talk about a 45-degree angle on a graph whose axes had different units. But in relativity, the symmetric appearance of the transformation tells us that space and time ought to be treated on the same footing, and measured in the same units.
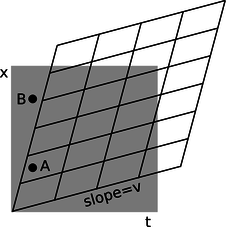
i / Interpretation of the Lorentz transformation. The slope indicated in the figure gives the relative velocity of the two frames of reference. Events A and B that were simultaneous in frame 1 are not simultaneous in frame 2, where event A occurs to the right of the \(t=0\) line represented by the left edge of the grid, but event B occurs to its left.
As in our discussion of the Galilean transformation, slopes are interpreted as velocities, and the slope of the near-horizontal lines in figure i is interpreted as the relative velocity of the two observers. The difference between the Galilean version and the relativistic one is that now there is smooshing happening from the other side as well. Lines that were vertical in the original grid, representing simultaneous events, now slant over to the right. This tells us that, as required by property 5, different observers do not agree on whether events that occur in different places are simultaneous. The Hafele-Keating experiment tells us that this non-simultaneity effect is fairly small, even when the velocity is as big as that of a passenger jet, and this is what we would have anticipated by the correspondence principle. The way that this is expressed in the graph is that if we pick the time unit to be the second, then the distance unit turns out to be hundreds of thousands of miles. In these units, the velocity of a passenger jet is an extremely small number, so the slope \(v\) in figure i is extremely small, and the amount of distortion is tiny --- it would be much too small to see on this scale.
The only thing left to determine about the Lorentz transformation is the size of the transformed parallelogram relative to the size of the original one. Although the drawing of the hands in figure h may suggest that the grid deforms like a framework made of rigid coat-hanger wire, that is not the case. If you look carefully at the figure, you'll see that the edges of the smooshed parallelogram are actually a little longer than the edges of the original rectangle. In fact what stays the same is not lengths but areas, as proved in the caption to figure j.
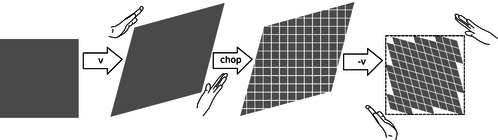
j / Proof that Lorentz transformations don't change area: We first subject a square to a transformation with velocity \(v\), and this increases its area by a factor \(R(v)\), which we want to prove equals 1. We chop the resulting parallelogram up into little squares and finally apply a \(-v\) transformation; this changes each little square's area by a factor \(R(-v)\), so the whole figure's area is also scaled by \(R(-v)\). The final result is to restore the square to its original shape and area, so \(R(v)R(-v)=1\). But \(R(v)=R(-v)\) by property 2 of spacetime on page 385, which states that all directions in space have the same properties, so \(R(v)=1\).
7.2.2 The \(\gamma\) factor
With a little algebra and geometry (homework problem 7, page 439), one can use the equal-area property to show that the factor \(\gamma\) (Greek letter gamma) defined in figure k is given by the equation
If you've had good training in physics, the first thing you probably think when you look at this equation is that it must be nonsense, because its units don't make sense. How can we take something with units of velocity squared, and subtract it from a unitless 1? But remember that this is expressed in our special relativistic units, in which the same units are used for distance and time. In this system, velocities are always unitless. This sort of thing happens frequently in physics. For instance, before James Joule discovered conservation of energy, nobody knew that heat and mechanical energy were different forms of the same thing, so instead of measuring them both in units of joules as we would do now, they measured heat in one unit (such as calories) and mechanical energy in another (such as foot-pounds). In ordinary metric units, we just need an extra conversion factor \(c\), and the equation becomes
Here's why we care about \(\gamma\). Figure k defines it as the ratio of two times: the time between two events as expressed in one coordinate system, and the time between the same two events as measured in the other one. The interpretation is:
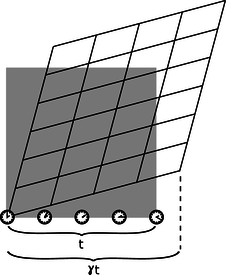
k / The \(\gamma\) factor.
Time dilation
A clock runs fastest in the frame of reference of an observer who is at rest relative to the clock. An observer in motion relative to the clock at speed \(v\) perceives the clock as running more slowly by a factor of \(\gamma\).
As proved in figures l and m, lengths are also distorted:
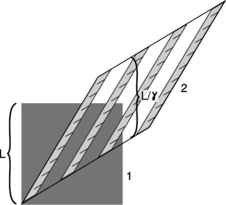
l / The ruler is moving in frame 1, represented by a square, but at rest in frame 2, shown as a parallelogram. Each picture of the ruler is a snapshot taken at a certain moment as judged according to frame 2's notion of simultaneity. An observer in frame 1 judges the ruler's length instead according to frame 1's definition of simultaneity, i.e., using points that are lined up vertically on the graph. The ruler appears shorter in the frame in which it is moving. As proved in figure m, the length contracts from \(L\) to \(L/\gamma\).
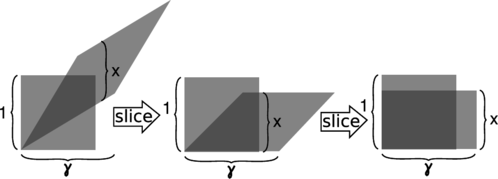
m / This figure proves, as claimed in figure l, that the length contraction is \(x=1/\gamma\). First we slice the parallelogram vertically like a salami and slide the slices down, making the top and bottom edges horizontal. Then we do the same in the horizontal direction, forming a rectangle with sides \(\gamma\) and \(x\). Since both the Lorentz transformation and the slicing processes leave areas unchanged, the area \(\gamma x\) of the rectangle must equal the area of the original square, which is 1.
Length contraction
A meter-stick appears longest to an observer who is at rest relative to it. An observer moving relative to the meter-stick at \(v\) observes the stick to be shortened by a factor of \(\gamma\).
Exercise \(\PageIndex{1}\)
What is \(\gamma\) when \(v=0\)? What does this mean?
(answer in the back of the PDF version of the book)
Example \(\PageIndex{1}\): An interstellar road trip
Alice stays on earth while her twin Betty heads off in a spaceship for Tau Ceti, a nearby star. Tau Ceti is 12 light-years away, so even though Betty travels at 87% of the speed of light, it will take her a long time to get there: 14 years, according to Alice.

n / Example 1.
Betty experiences time dilation. At this speed, her \(\gamma\) is 2.0, so that the voyage will only seem to her to last 7 years. But there is perfect symmetry between Alice's and Betty's frames of reference, so Betty agrees with Alice on their relative speed; Betty sees herself as being at rest, while the sun and Tau Ceti both move backward at 87% of the speed of light. How, then, can she observe Tau Ceti to get to her in only 7 years, when it should take 14 years to travel 12 light-years at this speed?
We need to take into account length contraction. Betty sees the distance between the sun and Tau Ceti to be shrunk by a factor of 2. The same thing occurs for Alice, who observes Betty and her spaceship to be foreshortened.
Example \(\PageIndex{2}\): Large time dilation
The time dilation effect in the Hafele-Keating experiment was very small. If we want to see a large time dilation effect, we can't do it with something the size of the atomic clocks they used; the kinetic energy would be greater than the total megatonnage of all the world's nuclear arsenals. We can, however, accelerate subatomic particles to speeds at which \(\gamma\) is large. For experimental particle physicists, relativity is something you do all day before heading home and stopping off at the store for milk. An early, low-precision experiment of this kind was performed by Rossi and Hall in 1941, using naturally occurring cosmic rays. Figure p shows a 1974 experiment2 of a similar type which verified the time dilation predicted by relativity to a precision of about one part per thousand.
Particles called muons (named after the Greek letter \(\mu\), “myoo”) were produced by an accelerator at CERN, near Geneva. A muon is essentially a heavier version of the electron. Muons undergo radioactive decay, lasting an average of only 2.197 \(\mu\text{s}\) before they evaporate into an electron and two neutrinos. The 1974 experiment was actually built in order to measure the magnetic properties of muons, but it produced a high-precision test of time dilation as a byproduct. Because muons have the same electric charge as electrons, they can be trapped using magnetic fields. Muons were injected into the ring shown in figure p, circling around it until they underwent radioactive decay. At the speed at which these muons were traveling, they had \(\gamma=29.33\), so on the average they lasted 29.33 times longer than the normal lifetime. In other words, they were like tiny alarm clocks that self-destructed at a randomly selected time. Figure o shows the number of radioactive decays counted, as a function of the time elapsed after a given stream of muons was injected into the storage ring. The two dashed lines show the rates of decay predicted with and without relativity. The relativistic line is the one that agrees with experiment.
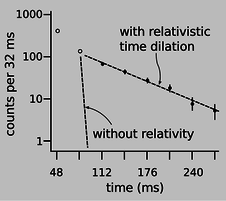
o / Muons accelerated to nearly \(c\) undergo radioactive decay much more slowly than they would according to an observer at rest with respect to the muons. The first two data-points (unfilled circles) were subject to large systematic errors.

p / Apparatus used for the test of relativistic time dilation described in example 2. The prominent black and white blocks are large magnets surrounding a circular pipe with a vacuum inside. (c) 1974 by CERN.
Example \(\PageIndex{3}\): An example of length contraction
Figure q shows an artist's rendering of the length contraction for the collision of two gold nuclei at relativistic speeds in the RHIC accelerator in Long Island, New York, which went on line in 2000. The gold nuclei would appear nearly spherical (or just slightly lengthened like an American football) in frames moving along with them, but in the laboratory's frame, they both appear drastically foreshortened as they approach the point of collision. The later pictures show the nuclei merging to form a hot soup, in which experimenters hope to observe a new form of matter.
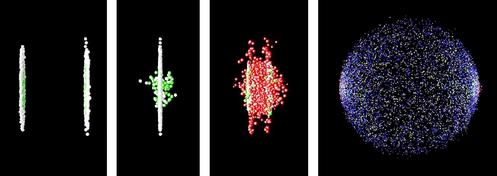
q / Colliding nuclei show relativistic length contraction.
Example \(\PageIndex{1}\): The garage paradox
One of the most famous of all the so-called relativity paradoxes has to do with our incorrect feeling that simultaneity is well defined. The idea is that one could take a schoolbus and drive it at relativistic speeds into a garage of ordinary size, in which it normally would not fit. Because of the length contraction, the bus would supposedly fit in the garage. The driver, however, will perceive the garage as being contracted and thus even less able to contain the bus.
The paradox is resolved when we recognize that the concept of fitting the bus in the garage “all at once” contains a hidden assumption, the assumption that it makes sense to ask whether the front and back of the bus can simultaneously be in the garage. Observers in different frames of reference moving at high relative speeds do not necessarily agree on whether things happen simultaneously. As shown in figure r, the person in the garage's frame can shut the door at an instant B he perceives to be simultaneous with the front bumper's arrival A at the back wall of the garage, but the driver would not agree about the simultaneity of these two events, and would perceive the door as having shut long after she plowed through the back wall.
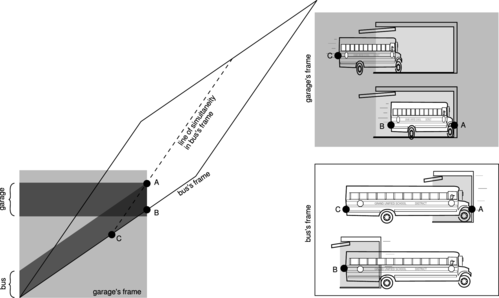
r / Example 4: In the garage's frame of reference, the bus is moving, and can fit in the garage due to its length contraction. In the bus's frame of reference, the garage is moving, and can't hold the bus due to its length contraction.
7.2.3 The universal speed \(c\)
Let's think a little more about the role of the 45-degree diagonal in the Lorentz transformation. Slopes on these graphs are interpreted as velocities. This line has a slope of 1 in relativistic units, but that slope corresponds to \(c\) in ordinary metric units. We already know that the relativistic distance unit must be extremely large compared to the relativistic time unit, so \(c\) must be extremely large. Now note what happens when we perform a Lorentz transformation: this particular line gets stretched, but the new version of the line lies right on top of the old one, and its slope stays the same. In other words, if one observer says that something has a velocity equal to \(c\), every other observer will agree on that velocity as well. (The same thing happens with \(-c\).)
Velocities don't simply add and subtract.
This is counterintuitive, since we expect velocities to add and subtract in relative motion. If a dog is running away from me at 5 m/s relative to the sidewalk, and I run after it at 3 m/s, the dog's velocity in my frame of reference is 2 m/s. According to everything we have learned about motion, the dog must have different speeds in the two frames: 5 m/s in the sidewalk's frame and 2 m/s in mine. But velocities are measured by dividing a distance by a time, and both distance and time are distorted by relativistic effects, so we actually shouldn't expect the ordinary arithmetic addition of velocities to hold in relativity; it's an approximation that's valid at velocities that are small compared to \(c\).
A universal speed limit
For example, suppose Janet takes a trip in a spaceship, and accelerates until she is moving at \(0.6c\) relative to the earth. She then launches a space probe in the forward direction at a speed relative to her ship of \(0.6c\). We might think that the probe was then moving at a velocity of \(1.2c\), but in fact the answer is still less than \(c\) (problem 1, page 438). This is an example of a more general fact about relativity, which is that \(c\) represents a universal speed limit. This is required by causality, as shown in figure s.
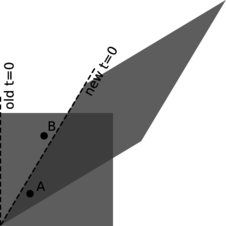
s / A proof that causality imposes a universal speed limit. In the original frame of reference, represented by the square, event A happens a little before event B. In the new frame, shown by the parallelogram, A happens after \(t=0\), but B happens before \(t=0\); that is, B happens before A. The time ordering of the two events has been reversed. This can only happen because events A and B are very close together in time and fairly far apart in space. The line segment connecting A and B has a slope greater than 1, meaning that if we wanted to be present at both events, we would have to travel at a speed greater than \(c\) (which equals 1 in the units used on this graph). You will find that if you pick any two points for which the slope of the line segment connecting them is less than 1, you can never get them to straddle the new \(t=0\) line in this funny, time-reversed way. Since different observers disagree on the time order of events like A and B, causality requires that information never travel from A to B or from B to A; if it did, then we would have time-travel paradoxes. The conclusion is that \(c\) is the maximum speed of cause and effect in relativity.
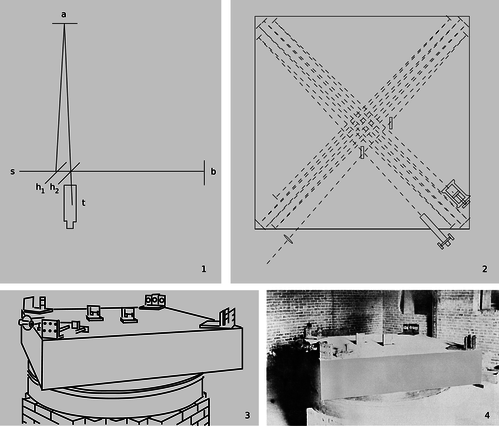
t / The Michelson-Morley experiment, shown in photographs, and drawings from the original 1887 paper. 1. A simplified drawing of the apparatus. A beam of light from the source, s, is partially reflected and partially transmitted by the half-silvered mirror \(\text{h}_1\). The two half-intensity parts of the beam are reflected by the mirrors at a and b, reunited, and observed in the telescope, t. If the earth's surface was supposed to be moving through the ether, then the times taken by the two light waves to pass through the moving ether would be unequal, and the resulting time lag would be detectable by observing the interference between the waves when they were reunited. 2. In the real apparatus, the light beams were reflected multiple times. The effective length of each arm was increased to 11 meters, which greatly improved its sensitivity to the small expected difference in the speed of light. 3. In an earlier version of the experiment, they had run into problems with its “extreme sensitiveness to vibration,” which was “so great that it was impossible to see the interference fringes except at brief intervals ... even at two o'clock in the morning.” They therefore mounted the whole thing on a massive stone floating in a pool of mercury, which also made it possible to rotate it easily. 4. A photo of the apparatus.
Light travels at \(c\).
Now consider a beam of light. We're used to talking casually about the “speed of light,” but what does that really mean? Motion is relative, so normally if we want to talk about a velocity, we have to specify what it's measured relative to. A sound wave has a certain speed relative to the air, and a water wave has its own speed relative to the water. If we want to measure the speed of an ocean wave, for example, we should make sure to measure it in a frame of reference at rest relative to the water. But light isn't a vibration of a physical medium; it can propagate through the near-perfect vacuum of outer space, as when rays of sunlight travel to earth. This seems like a paradox: light is supposed to have a specific speed, but there is no way to decide what frame of reference to measure it in. The way out of the paradox is that light must travel at a velocity equal to \(c\). Since all observers agree on a velocity of \(c\), regardless of their frame of reference, everything is consistent.
The Michelson-Morley experiment
The constancy of the speed of light had in fact already been observed when Einstein was an 8-year-old boy, but because nobody could figure out how to interpret it, the result was largely ignored. In 1887 Michelson and Morley set up a clever apparatus to measure any difference in the speed of light beams traveling east-west and north-south. The motion of the earth around the sun at 110,000 km/hour (about 0.01% of the speed of light) is to our west during the day. Michelson and Morley believed that light was a vibration of a mysterious medium called the ether, so they expected that the speed of light would be a fixed value relative to the ether. As the earth moved through the ether, they thought they would observe an effect on the velocity of light along an east-west line. For instance, if they released a beam of light in a westward direction during the day, they expected that it would move away from them at less than the normal speed because the earth was chasing it through the ether. They were surprised when they found that the expected 0.01% change in the speed of light did not occur.
Example \(\PageIndex{4}\): The ring laser gyroscope
If you've flown in a jet plane, you can thank relativity for helping you to avoid crashing into a mountain or an ocean. Figure u shows a standard piece of navigational equipment called a ring laser gyroscope. A beam of light is split into two parts, sent around the perimeter of the device, and reunited. Since the speed of light is constant, we expect the two parts to come back together at the same time. If they don't, it's evidence that the device has been rotating. The plane's computer senses this and notes how much rotation has accumulated.

u / A ring laser gyroscope.
Example \(\PageIndex{6}\): No frequency-dependence
Relativity has only one universal speed, so it requires that all light waves travel at the same speed, regardless of their frequency and wavelength. Presently the best experimental tests of the invariance of the speed of light with respect to wavelength come from astronomical observations of gamma-ray bursts, which are sudden outpourings of high-frequency light, believed to originate from a supernova explosion in another galaxy. One such observation, in 2009,3 found that the times of arrival of all the different frequencies in the burst differed by no more than 2 seconds out of a total time in flight on the order of ten billion years!
Discussion Questions
◊

Discussion question B.
A question that students often struggle with is whether time and space can really be distorted, or whether it just seems that way. Compare with optical illusions or magic tricks. How could you verify, for instance, that the lines in the figure are actually parallel? Are relativistic effects the same, or not?
◊ On a spaceship moving at relativistic speeds, would a lecture seem even longer and more boring than normal?
◊ Mechanical clocks can be affected by motion. For example, it was a significant technological achievement to build a clock that could sail aboard a ship and still keep accurate time, allowing longitude to be determined. How is this similar to or different from relativistic time dilation?
◊ Figure q from page 392, depicting the collision of two nuclei at the RHIC accelerator, is reproduced below. What would the shapes of the two nuclei look like to a microscopic observer riding on the left-hand nucleus? To an observer riding on the right-hand one? Can they agree on what is happening? If not, why not --- after all, shouldn't they see the same thing if they both compare the two nuclei side-by-side at the same instant in time?

v / Discussion question E: colliding nuclei show relativistic length contraction.
◊ The machine-gunner in the figure sends out a spray of bullets. Suppose that the bullets are being shot into outer space, and that the distances traveled are trillions of miles (so that the human figure in the diagram is not to scale). After a long time, the bullets reach the points shown with dots which are all equally far from the gun. Their arrivals at those points are events A through E, which happen at different times. The chain of impacts extends across space at a speed greater than \(c\). Does this violate special relativity?
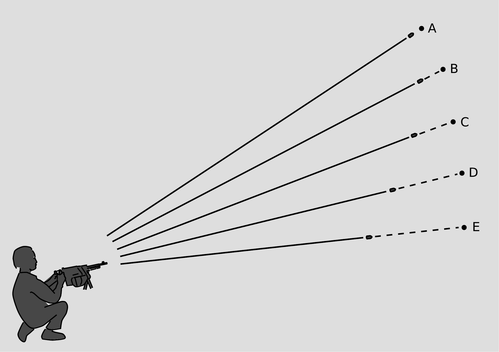
Discussion question G.
7.2.4 No action at a distance
The Newtonian picture
The Newtonian picture of the universe has particles interacting with each other by exerting forces from a distance, and these forces are imagined to occur without any time delay. For example, suppose that super-powerful aliens, angered when they hear disco music in our AM radio transmissions, come to our solar system on a mission to cleanse the universe of our aesthetic contamination. They apply a force to our sun, causing it to go flying out of the solar system at a gazillion miles an hour. According to Newton's laws, the gravitational force of the sun on the earth will immediately start dropping off. This will be detectable on earth, and since sunlight takes eight minutes to get from the sun to the earth, the change in gravitational force will, according to Newton, be the first way in which earthlings learn the bad news --- the sun will not visibly start receding until a little later. Although this scenario is fanciful, it shows a real feature of Newton's laws: that information can be transmitted from one place in the universe to another with zero time delay, so that transmission and reception occur at exactly the same instant. Newton was sharp enough to realize that this required a nontrivial assumption, which was that there was some completely objective and well-defined way of saying whether two things happened at exactly the same instant. He stated this assumption explicitly: “Absolute, true, and mathematical time, of itself, and from its own nature flows at a constant rate without regard to anything external...”
Time delays in forces exerted at a distance
Relativity forbids Newton's instantaneous action at a distance. For suppose that instantaneous action at a distance existed. It would then be possible to send signals from one place in the universe to another without any time lag. This would allow perfect synchronization of all clocks. But the Hafele-Keating experiment demonstrates that clocks A and B that have been initially synchronized will drift out of sync if one is in motion relative to the other. With instantaneous transmission of signals, we could determine, without having to wait for A and B to be reunited, which was ahead and which was behind. Since they don't need to be reunited, neither one needs to undergo any acceleration; each clock can fix an inertial frame of reference, with a velocity vector that changes neither its direction nor its magnitude. But this violates the principle that constant-velocity motion is relative, because each clock can be considered to be at rest, in its own frame of reference. Since no experiment has ever detected any violation of the relativity of motion, we conclude that instantaneous action at a distance is impossible.
Since forces can't be transmitted instantaneously, it becomes natural to imagine force-effects spreading outward from their source like ripples on a pond, and we then have no choice but to impute some physical reality to these ripples. We call them fields, and they have their own independent existence. Gravity is transmitted through a field called the gravitational field. Besides gravity, there are other fundamental fields of force such as electricity and magnetism (ch. 10-11). Ripples of the electric and magnetic fields turn out to be light waves. This tells us that the speed at which electric and magnetic field ripples spread must be \(c\), and by an argument similar to the one in subsection 7.2.3 the same must hold for any other fundamental field, including the gravitational field.
Fields don't have to wiggle; they can hold still as well. The earth's magnetic field, for example, is nearly constant, which is why we can use it for direction-finding.
Even empty space, then, is not perfectly featureless. It has measurable properties. For example, we can drop a rock in order to measure the direction of the gravitational field, or use a magnetic compass to find the direction of the magnetic field. This concept made a deep impression on Einstein as a child. He recalled that as a five-year-old, the gift of a magnetic compass convinced him that there was “something behind things, something deeply hidden.”
More evidence that fields of force are real: they carry energy.
w / Fields carry energy.
The smoking-gun argument for this strange notion of traveling force ripples comes from the fact that they carry energy. In figure x/1, Alice and Betty hold balls A and B at some distance from one another. These balls make a force on each other; it doesn't really matter for the sake of our argument whether this force is gravitational, electrical, or magnetic. Let's say it's electrical, i.e., that the balls have the kind of electrical charge that sometimes causes your socks to cling together when they come out of the clothes dryer. We'll say the force is repulsive, although again it doesn't really matter.
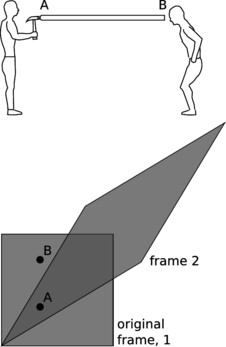
x / Discussion question E.
If Alice chooses to move her ball closer to Betty's, x/2, Alice will have to do some mechanical work against the electrical repulsion, burning off some of the calories from that chocolate cheesecake she had at lunch. This reduction in her body's chemical energy is offset by a corresponding increase in the electrical interaction energy. Not only that, but Alice feels the resistance stiffen as the balls get closer together and the repulsion strengthens. She has to do a little extra work, but this is all properly accounted for in the interaction energy.
But now suppose, x/3, that Betty decides to play a trick on Alice by tossing B far away just as Alice is getting ready to move A. We have already established that Alice can't feel B's motion instantaneously, so the electric forces must actually be propagated by an electric field. Of course this experiment is utterly impractical, but suppose for the sake of argument that the time it takes the change in the electric field to propagate across the diagram is long enough so that Alice can complete her motion before she feels the effect of B's disappearance. She is still getting stale information about B's position. As she moves A to the right, she feels a repulsion, because the field in her region of space is still the field caused by B in its old position. She has burned some chocolate cheesecake calories, and it appears that conservation of energy has been violated, because these calories can't be properly accounted for by any interaction with B, which is long gone.
If we hope to preserve the law of conservation of energy, then the only possible conclusion is that the electric field itself carries away the cheesecake energy. In fact, this example represents an impractical method of transmitting radio waves. Alice does work on charge A, and that energy goes into the radio waves. Even if B had never existed, the radio waves would still have carried energy, and Alice would still have had to do work in order to create them.
Discussion Questions

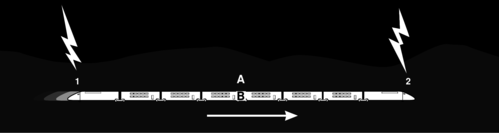
◊ Use a graph to resolve the following relativity paradox. Relativity says that in one frame of reference, event A could happen before event B, but in someone else's frame B would come before A. How can this be? Obviously the two people could meet up at A and talk as they cruised past each other. Wouldn't they have to agree on whether B had already happened?
◊ The rod in the figure is perfectly rigid. At event A, the hammer strikes one end of the rod. At event B, the other end moves. Since the rod is perfectly rigid, it can't compress, so A and B are simultaneous. In frame 2, B happens before A. Did the motion at the right end cause the person on the left to decide to pick up the hammer and use it?
7.2.5 The light cone
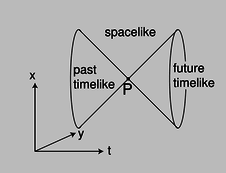
y / The light cone.
Given an event P, we can now classify all the causal relationships in which P can participate. In Newtonian physics, these relationships fell into two classes: P could potentially cause any event that lay in its future, and could have been caused by any event in its past. In relativity, we have a three-way distinction rather than a two-way one. There is a third class of events that are too far away from P in space, and too close in time, to allow any cause and effect relationship, since causality's maximum velocity is \(c\). Since we're working in units in which \(c=1\), the boundary of this set is formed by the lines with slope \(\pm1\) on a \((t,x)\) plot. This is referred to as the light cone, for reasons that become more visually obvious when we consider more than one spatial dimension, figure aa.
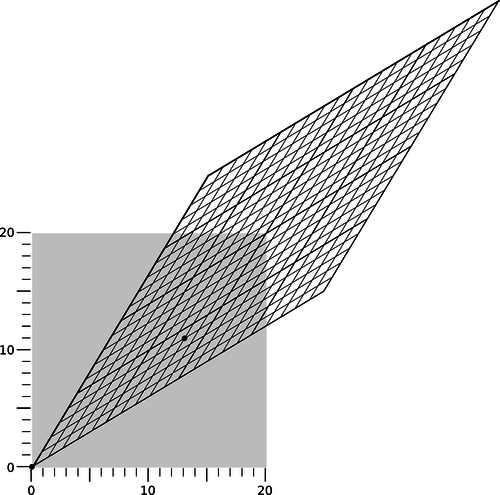
aa / Example 9.
Events lying inside one another's light cones are said to have a timelike relationship. Events outside each other's light cones are spacelike in relation to one another, and in the case where they lie on the surfaces of each other's light cones the term is lightlike. \myoptionalsubsection[2]{The spacetime interval}
The light cone is an object of central importance in both special and general relativity. It relates the geometry of spacetime to possible cause-and-effect relationships between events. This is fundamentally how relativity works: it's a geometrical theory of causality.
These ideas naturally lead us to ask what fruitful analogies we can form between the bizarre geometry of spacetime and the more familiar geometry of the Euclidean plane. The light cone cuts spacetime into different regions according to certain measurements of relationships between points (events). Similarly, a circle in Euclidean geometry cuts the plane into two parts, an interior and an exterior, according to the measurement of the distance from the circle's center. A circle stays the same when we rotate the plane. A light cone stays the same when we change frames of reference. Let's build up the analogy more explicitly.
Measurement in Euclidean geometry
We say that two line segments are congruent, \(\text{AB}\cong \text{CD}\), if the distance between points A and B is the same as the distance between C and D, as measured by a rigid ruler.
Measurement in spacetime
We define \(\text{AB}\cong \text{CD}\) if:
- AB and CD are both spacelike, and the two distances are equal as measured by a rigid ruler, in a frame where the two events touch the ruler simultaneously.
- AB and CD are both timelike, and the two time intervals are equal as measured by clocks moving inertially.
- AB and CD are both lightlike.
The three parts of the relativistic version each require some justification.
Case 1 has to be the way it is because space is part of spacetime. In special relativity, this space is Euclidean, so the definition of congruence has to agree with the Euclidean definition, in the case where it is possible to apply the Euclidean definition. The spacelike relation between the points is both necessary and sufficient to make this possible. If points A and B are spacelike in relation to one another, then a frame of reference exists in which they are simultaneous, so we can use a ruler that is at rest in that frame to measure their distance. If they are lightlike or timelike, then no such frame of reference exists. For example, there is no frame of reference in which Charles VII's restoration to the throne is simultaneous with Joan of Arc's execution, so we can't arrange for both of these events to touch the same ruler at the same time.
The definition in case 2 is the only sensible way to proceed if we are to respect the symmetric treatment of time and space in relativity. The timelike relation between the events is necessary and sufficient to make it possible for a clock to move from one to the other. It makes a difference that the clocks move inertially, because the twins in example 1 on p. 391 disagree on the clock time between the traveling twin's departure and return.
Case 3 may seem strange, since it says that any two lightlike intervals are congruent. But this is the only possible definition, because this case can be obtained as a limit of the timelike one. Suppose that AB is a timelike interval, but in the planet earth's frame of reference it would be necessary to travel at almost the speed of light in order to reach B from A. The required speed is less than \(c\) (i.e., less than 1) by some tiny amount \(\epsilon\). In the earth's frame, the clock referred to in the definition suffers extreme time dilation. The time elapsed on the clock is very small. As \(\epsilon\) approaches zero, and the relationship between A and B approaches a lightlike one, this clock time approaches zero. In this sense, the relativistic notion of “distance” is very different from the Euclidean one. In Euclidean geometry, the distance between two points can only be zero if they are the same point.
The case splitting involved in the relativistic definition is a little ugly. Having worked out the physical interpretation, we can now consolidate the definition in a nicer way by appealing to Cartesian coordinates.
Cartesian definition of distance in Euclidean geometry
Given a vector \((\Delta x,\Delta y)\) from point A to point B, the square of the distance between them is defined as \(\overline{\text{AB}}^2=\Delta x^2+\Delta y^2\).
Definition of the interval in relativity
Given points separated by coordinate differences \(\Delta x\), \(\Delta y\), \(\Delta z\), and \(\Delta t\), the spacetime interval \(\mathcal I\) (cursive letter “I”) between them is defined as \(\mathcal I = \Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2\).
This is stated in natural units, so all four terms on the right-hand side have the same units; in metric units with \(c \ne 1\), appropriate factors of \(c\) should be inserted in order to make the units of the terms agree. The interval \(\mathcal I\) is positive if AB is timelike (regardless of which event comes first), zero if lightlike, and negative if spacelike. Since \(\mathcal I\) can be negative, we can't in general take its square root and define a real number \(\overline{\text{AB}}\) as in the Euclidean case. When the interval is timelike, we can interpret \(\sqrt{\mathcal I}\) as a time, and when it's spacelike we can take \(\sqrt{-\mathcal I}\) to be a distance.
The Euclidean definition of distance (i.e., the Pythagorean theorem) is useful because it gives the same answer regardless of how we rotate the plane. Although it is stated in terms of a certain coordinate system, its result is unambiguously defined because it is the same regardless of what coordinate system we arbitrarily pick. Similarly, \(\mathcal I\) is useful because, as proved in example 8 below, it is the same regardless of our frame of reference, i.e., regardless of our choice of coordinates.
Example \(\PageIndex{7}\): Pioneer 10
\(\triangleright\) The Pioneer 10 space probe was launched in 1972, and in 1973 was the first craft to fly by the planet Jupiter. It crossed the orbit of the planet Neptune in 1983, after which telemetry data were received until 2002. The following table gives the spacecraft's position relative to the sun at exactly midnight on January 1, 1983 and January 1, 1995. The 1983 date is taken to be \(t=0\).
| t (s) | x | y | z |
|---|---|---|---|
| 0 | 1.784 X 1012 m | 3.951 X 1012 m | 0.237 X 1012 m |
| 3.7869120000 X 108 s | 2.420 X 1012 m | 8.827 X 1012 m | 0.488 X 1012 m |
Compare the time elapsed on the spacecraft to the time in a frame of reference tied to the sun.
\(\triangleright\) We can convert these data into natural units, with the distance unit being the second (i.e., a light-second, the distance light travels in one second) and the time unit being seconds. Converting and carrying out this subtraction, we have:
| Δt (s) | Δx | Δy | Δz |
|---|---|---|---|
| 3.7869120000 X 108 s | 0.212 X 104 s | 1.626 X 104 s | 0.084 X 104 s |
Comparing the exponents of the temporal and spatial numbers, we can see that the spacecraft was moving at a velocity on the order of \(10^{-4}\) of the speed of light, so relativistic effects should be small but not completely negligible.
Since the interval is timelike, we can take its square root and interpret it as the time elapsed on the spacecraft. The result is \(\sqrt{\mathcal I}=3.786911996\times 10^8\ \text{s}\). This is 0.4 s less than the time elapsed in the sun's frame of reference.
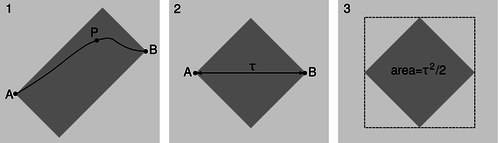
z / Light-rectangles, example 8.
1. The gray light-rectangle represents the set of all events such as P that could be visited after A and before B.
2. The rectangle becomes a square in the frame in which A and B occur at the same location in space.
3. The area of the dashed square is \(\tau^2\), so the area of the gray square is \(\tau^2/2\).
Example \(\PageIndex{8}\): Invariance of the interval
In this example we prove that the interval is the same regardless of what frame of reference we compute it in. This is called “Lorentz invariance.” The proof is limited to the timelike case. Given events A and B, construct the light-rectangle as defined in figure ab/1. On p. 389 we proved that the Lorentz transformation doesn't change the area of a shape in the \(x\)-\(t\) plane. Therefore the area of this rectangle is unchanged if we switch to the frame of reference ab/2, in which A and B occurred at the same location and were separated by a time interval \(\tau\). This area equals half the interval \(\mathcal I\) between A and B. But a straightforward calculation shows that the rectangle in ab/1 also has an area equal to half the interval calculated in that frame. Since the area in any frame equals half the interval, and the area is the same in all frames, the interval is equal in all frames as well.
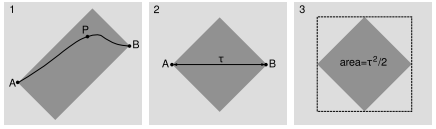
ab / Example 8.
Example \(\PageIndex{9}\): A numerical example of invariance
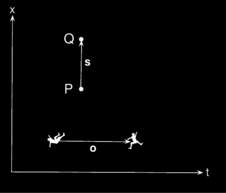
ac / Example 9.
Figure ac shows two frames of reference in motion relative to one another at \(v=3/5\). (For this velocity, the stretching and squishing of the main diagonals are both by a factor of 2.) Events are marked at coordinates that in the frame represented by the square are
The interval between these events is \(13^2-11^2=48\). In the frame represented by the parallelogram, the same two events lie at coordinates
Calculating the interval using these values, the result is
\(8^2-4^2=48\), which comes out the same as in the other frame.
Four-vectors and the inner product
Example 7 makes it natural that we define a type of vector with four components, the first one relating to time and the others being spatial. These are known as four-vectors. It's clear how we should define the equivalent of a dot product in relativity:
The term “dot product” has connotations of referring only to three-vectors, so the operation of taking the scalar product of two four-vectors is usually referred to instead as the “inner product.” The spacetime interval can then be thought of as the inner product of a four-vector with itself. We care about the relativistic inner product for exactly the same reason we care about its Euclidean version; both are scalars, so they have a fixed value regardless of what coordinate system we choose.
| Example 10: The twin paradox |
|---|
|
Alice and Betty are identical twins. Betty goes on a space voyage at relativistic speeds, traveling away from the earth and then turning around and coming back. Meanwhile, Alice stays on earth. When Betty returns, she is younger than Alice because of relativistic time dilation (example 1, p. 391). But isn't it valid to say that Betty's spaceship is standing still and the earth moving? In that description, wouldn't Alice end up younger and Betty older? This is referred to as the “twin paradox.” It can't really be a paradox, since it's exactly what was observed in the Hafele-Keating experiment (p. 381). Betty's track in the \(x\)-\(t\) plane (her “world-line” in relativistic jargon) consists of vectors \(\mathbf{b}\) and \(\mathbf{c}\) strung end-to-end (figure ad). We could adopt a frame of reference in which Betty was at rest during \(\mathbf{b}\) (i.e., \(b_x=0\)), but there is no frame in which \(\mathbf{b}\) and \(\mathbf{c}\) are parallel, so there is no frame in which Betty was at rest during both \(\mathbf{b}\) and \(\mathbf{c}\). This resolves the paradox. We have already established by other methods that Betty ages less that Alice, but let's see how this plays out in a simple numerical example. Omitting units and making up simple numbers, let's say that the vectors in figure ad are \[\begin{align*} \mathbf{a} &= (6,1) \\ \mathbf{b} &= (3,2) \\ \mathbf{c} &= (3,-1) , \end{align*}\]
where the components are given in the order \((t,x)\). The time experienced by Alice is then \[\begin{equation*} |\mathbf{a}| = \sqrt{6^2-1^2} =5.9 , \end{equation*}\]
which is greater than the Betty's elapsed time \[\begin{equation*} |\mathbf{b}|+|\mathbf{c}| = \sqrt{3^2-2^2}+\sqrt{3^2-(-1)^2} = 5.1 . \end{equation*}\]
|
| Example 11: Simultaneity using inner products |
|---|
|
ac / Example 11. Suppose that an observer O moves inertially along a vector \(\mathbf{o}\), and let the vector separating two events P and Q be \(\mathbf{s}\). O judges these events to be simultaneous if \(\mathbf{o}\cdot\mathbf{s}=0\). To see why this is true, suppose we pick a coordinate system as defined by O. In this coordinate system, O considers herself to be at rest, so she says her vector has only a time component, \(\mathbf{o}=(\Delta t,0,0,0)\). If she considers P and Q to be simultaneous, then the vector from P to Q is of the form \((0,\Delta x,\Delta y,\Delta z)\). The inner product is then zero, since each of the four terms vanishes. Since the inner product is independent of the choice of coordinate system, it doesn't matter that we chose one tied to O herself. Any other observer \(\text{O}'\) can look at O's motion, note that \(\mathbf{o}\cdot\mathbf{s}=0\), and infer that O must consider P and Q to be simultaneous, even if \(\text{O}'\) says they weren't. |
Doppler shifts of light and addition of velocities
When Doppler shifts happen to ripples on a pond or the sound waves from an airplane, they can depend on the relative motion of three different objects: the source, the receiver, and the medium. But light waves don't have a medium. Therefore Doppler shifts of light can only depend on the relative motion of the source and observer.

ad / The pattern of waves made by a point source moving to the right across the water. Note the shorter wavelength of the forward-emitted waves and the longer wavelength of the backward-going ones.
One simple case is the one in which the relative motion of the source and the receiver is perpendicular to the line connecting them. That is, the motion is transverse. Nonrelativistic Doppler shifts happen because the distance between the source and receiver is changing, so in nonrelativistic physics we don't expect any Doppler shift at all when the motion is transverse, and this is what is in fact observed to high precision. For example, the photo shows shortened and lengthened wavelengths to the right and left, along the source's line of motion, but an observer above or below the source measures just the normal, unshifted wavelength and frequency. But relativistically, we have a time dilation effect, so for light waves emitted transversely, there is a Doppler shift of \(1/\gamma\) in frequency (or \(\gamma\) in wavelength).
The other simple case is the one in which the relative motion of the source and receiver is longitudinal, i.e., they are either approaching or receding from one another. For example, distant galaxies are receding from our galaxy due to the expansion of the universe, and this expansion was originally detected because Doppler shifts toward the red (low-frequency) end of the spectrum were observed.
Nonrelativistically, we would expect the light from such a galaxy to be Doppler shifted down in frequency by some factor, which would depend on the relative velocities of three different objects: the source, the wave's medium, and the receiver. Relativistically, things get simpler, because light isn't a vibration of a physical medium, so the Doppler shift can only depend on a single velocity \(v\), which is the rate at which the separation between the source and the receiver is increasing.

ae / A graphical representation of the Lorentz transformation for a velocity of \((3/5)c\). The long diagonal is stretched by a factor of two, the short one is half its former length, and the area is the same as before.
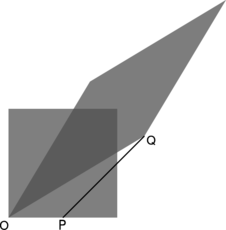
af / At event O, the source and the receiver are on top of each other, so as the source emits a wave crest, it is received without any time delay. At P, the source emits another wave crest, and at Q the receiver receives it.
The square in figure af is the “graph paper” used by someone who considers the source to be at rest, while the parallelogram plays a similar role for the receiver. The figure is drawn for the case where \(v=3/5\) (in units where \(c=1\)), and in this case the stretch factor of the long diagonal is 2. To keep the area the same, the short diagonal has to be squished to half its original size. But now it's a matter of simple geometry to show that OP equals half the width of the square, and this tells us that the Doppler shift is a factor of 1/2 in frequency. That is, the squish factor of the short diagonal is interpreted as the Doppler shift. To get this as a general equation for velocities other than 3/5, one can show by straightforward fiddling with the result of part c of problem 7 on p. 439 that the Doppler shift is
Here \(v>0\) is the case where the source and receiver are getting farther apart, \(v\lt0\) the case where they are approaching. (This is the opposite of the sign convention used in subsection 6.1.5. It is convenient to change conventions here so that we can use positive values of \(v\) in the case of cosmological red-shifts, which are the most important application.)
Suppose that Alice stays at home on earth while her twin Betty takes off in her rocket ship at 3/5 of the speed of light. When I first learned relativity, the thing that caused me the most pain was understanding how each observer could say that the other was the one whose time was slow. It seemed to me that if I could take a pill that would speed up my mind and my body, then naturally I would see everybody else as being slow. Shouldn't the same apply to relativity? But suppose Alice and Betty get on the radio and try to settle who is the fast one and who is the slow one. Each twin's voice sounds slooooowed doooowwwwn to the other. If Alice claps her hands twice, at a time interval of one second by her clock, Betty hears the hand-claps coming over the radio two seconds apart, but the situation is exactly symmetric, and Alice hears the same thing if Betty claps. Each twin analyzes the situation using a diagram identical to ah, and attributes her sister's observations to a complicated combination of time distortion, the time taken by the radio signals to propagate, and the motion of her twin relative to her.
self-check:
Turn your book upside-down and reinterpret figure ah.
(answer in the back of the PDF version of the book)
| Example 12: A symmetry property of the Doppler effect |
|---|
| Suppose that A and B are at rest relative to one another, but C is moving along the line between A and B. A transmits a signal to C, who then retransmits it to B. The signal accumulates two Doppler shifts, and the result is their product \(D(v)D(-v)\). But this product must equal 1, so we must have \(D(-v)D(v)=1\), which can be verified directly from the equation. |
| Example 13: The Ives-Stilwell experiment | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
The result of example 12 was the basis of one of the earliest laboratory tests of special relativity, by Ives and Stilwell in 1938. They observed the light emitted by excited by a beam of \(\text{H}_2^+\) and \(\text{H}_3^+\) ions with speeds of a few tenths of a percent of \(c\). Measuring the light from both ahead of and behind the beams, they found that the product of the Doppler shifts \(D(v)D(-v)\) was equal to 1, as predicted by relativity. If relativity had been false, then one would have expected the product to differ from 1 by an amount that would have been detectable in their experiment. In 2003, Saathoff et al. carried out an extremely precise version of the Ives-Stilwell technique with \(\text{Li}^+\) ions moving at 6.4% of \(c\). The frequencies observed, in units of MHz, were:
The results show incredibly precise agreement between \(f_\text{o}\) and \(\sqrt{f_\text{o}D(-v)\cdot f_\text{o} D(v)}\), as expected relativistically because \(D(v)D(-v)\) is supposed to equal 1. The agreement extends to 9 significant figures, whereas if relativity had been false there should have been a relative disagreement of about \(v^2=.004\), i.e., a discrepancy in the third significant figure. The spectacular agreement with theory has made this experiment a lightning rod for anti-relativity kooks. |
We saw on p. 394 that relativistic velocities should not be expected to be exactly additive, and problem 1 on p. 438 verifies this in the special case where A moves relative to B at \(0.6c\) and B relative to C at \(0.6c\) --- the result not being \(1.2c\). The relativistic Doppler shift provides a simple way of deriving a general equation for the relativistic combination of velocities; problem 17 on p. 442 guides you through the steps of this derivation, and the result is given on p. 936.
Contributors and Attributions
- Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


