02. Analysis Tools
- Page ID
- 663
Applying the Impulse-Momentum Relation to a Single Object
Let’s investigate the following scenario:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
To apply the impulse-momentum relation, you must clearly specify the initial and final events at which you will tabulate the momentum. Let’s choose:
Event 1: The instant the engine is ignited.
Event 2: The instant the engine shuts off.

Applying impulse-momentum to the rocket during this time interval yields:
\( mv_{i}+\sum F(\Delta t)=mv_{f} \)
\( .35(0)+F_{exhaust}(1.8)-F_{gravity}(1.8)=.35v_{2} \)
\( 0+ (11.8)(1.8)-(.35)(9.8)(1.8)=.35v_{2} \)
\( v_{2}=43.0 m/s \)
where each applied force is independently multiplied by the time interval over which it acts. (Note that the rocket’s engine does not produce a force on the rocket! The engine produces a downward force on the hot exhaust gases emitted from the engine and these hot gases exert an equal magnitude force back up on the rocket. That is why the force on the rocket is labeled as Fexhaust rather than Fengine.) Thus, the rocket is traveling at 43.0 m/s at the instant the engine shuts off.
Of course, there is no reason why we had to analyze the rocket’s motion between the two instants of time we selected above. We could have selected the events:
Event 1: The instant the engine is ignited.
Event 2: The instant the rocket reaches maximum height.
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire time interval. Noting that the rocket’s velocity when it reaches its maximum height is zero, impulse-momentum would look like this:
\( mv_{i}+\sum F(\Delta t)=mv_{f} \)
\( .35(0)+F_{exhaust}(1.8)-F_{gravity}(\Delta t)=(0.35)(0) \)
\( 0+ (11.8)(1.8)-(.35)(9.8)(\Delta t)=0 \)
\( \Delta t=6.19 s\)
Thus, the rocket is in the air for \( 6.19 s \) before reaching its maximum height.
Applying the Work-Energy Relation to a Single Object
The work-energy relation also has many uses for investigating physical scenarios. For example, let’s look again at our model rocket:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
To apply the work-energy relation, you must clearly specify the initial and final events at which you will tabulate the energy. Let’s choose:
Event 1: The instant the engine is ignited.
Event 2: The instant the engine shuts off.
 Assuming we’ve already analyzed this scenario using impulse-momentum, what additional information can we extract using work-energy?
Assuming we’ve already analyzed this scenario using impulse-momentum, what additional information can we extract using work-energy?
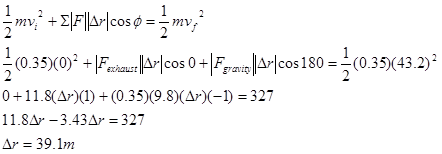
Thus, the rocket rises to a height of 39.1 m before the engines shuts off.
What if we apply work-energy between the following two events:
Event 1: The instant the engine is ignited.
Event 2: The instant the rocket reaches its maximum height.
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire displacement, namely 39 m, while the force of gravity acts over the entire displacement.
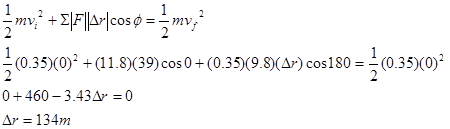
Thus, the maximum height reached by the rocket is 134 m.


