03. Drawing Motion Graphs
- Page ID
- 465
Let’s look at the situation again:
In the shot put, a large mass is thrown at an angle of 22oabove horizontal, from a position of 2 m above the ground, a horizontal distance of 25 m.
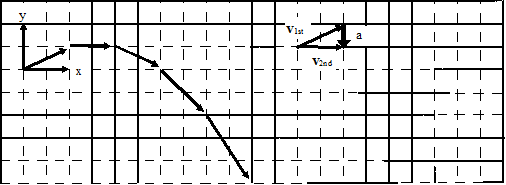
The verbal representation of the situation has already been translated into a pictorial representation, the motion diagram. A careful reading of the motion diagram allows the construction of the motion graphs.
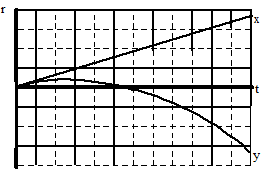
Drawing the position vs. time graph
First, examine the position of the shot put as it moves through the air. Remember, the analysis of the horizontal position must be independent of the analysis of the vertical position.
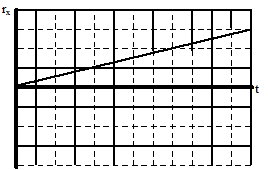
Horizontal Position
From the motion diagram, the shot put starts at position zero, and then has positive, increasing positions throughout the remainder of its motion. The horizontal position increases by even amounts in even time intervals.
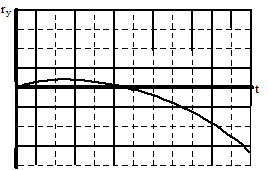
Vertical Position
The shot put starts at position zero, increases its vertical position at a rate that is decreasing, then begins to decrease its vertical position at a rate that is increasing, even as it drops to negative positions.
Typically, both the horizontal and vertical positions are displayed on the same axis.
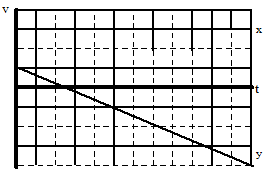
Drawing the velocity vs. time graph
In the horizontal direction, the rate at which the position changes is constant. Hence, the horizontal component of velocity is constant, and positive. In the vertical direction, the velocity component begins positive, decreases to zero, and then increases in the negative direction.
Drawing the acceleration vs. time graph
From the motion diagram, the acceleration of the shot-put can be determined to be directed downward at every point. Thus, the horizontal component of acceleration is zero and the vertical component is negative, and approximately constant due to our model's approximations.