05. Circular Motion 2
- Page ID
- 445
Polar Coordinates
In the polar coordinate system, one axis (the radial axis, or 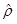 is perpendicular to the surface of the circular path pointing radially away from the center, and the other axis (the tangential, or
is perpendicular to the surface of the circular path pointing radially away from the center, and the other axis (the tangential, or 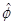 is parallel to the surface of the circular path pointing in the counterclockwise direction. (r is the lower-case Greek letter "rho" and f is "phi".)
is parallel to the surface of the circular path pointing in the counterclockwise direction. (r is the lower-case Greek letter "rho" and f is "phi".)
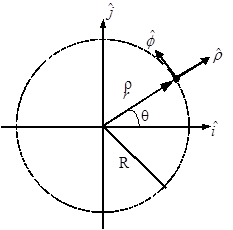
Notice that ![]() is inclined by an angle q from the positive x-axis. Therefore, in terms of
is inclined by an angle q from the positive x-axis. Therefore, in terms of  and
and 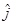 ;
;
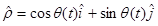
![]() , on the other hand, is inclined by an angle q to the left of the positive y-axis. Therefore, in terms of
, on the other hand, is inclined by an angle q to the left of the positive y-axis. Therefore, in terms of ![]() and
and ![]() ;
;
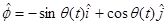
Now re-examine the relationships for position, velocity and acceleration.
Position
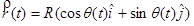
becomes
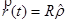
In component form this is:
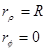
This means that the position of an object undergoing circular motion is only in the radial direction, and has a constant magnitude equal to the radius of the circle. Basically, the coordinate system is constructed so that the location of the object defines the radial direction.
Velocity
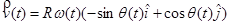
becomes
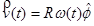
In component form this is:
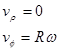
This means that the velocity of an object undergoing circular motion is only in the tangential direction, and has a magnitude equal to the product of the radius and angular velocity. The only way an object can have a radial velocity is if the radius of it path changes, but that can't happen for an object moving along a circular path. If the object moved along an elliptical path, for example, then it would have both tangential and radial velocities.
Acceleration
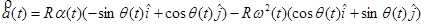
becomes
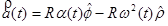
In component form this is:
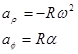
The acceleration of an object undergoing circular motion has two components. If the object is speeding up or slowing down, the angular acceleration does not equal zero and there is an acceleraton component in the tangential direction. The magnitude of the tangential acceleration is equal to the product of the radius and angular acceleration.
However, even if the object is moving at constant speed, there is an acceleration component in the negative radial direction, i.e., pointing toward the center of the circle. By virtue of traveling in a circle, the velocity vector of an object continually changes its orientation. This change in orientation is directed toward the center of the circle. Draw a motion diagram and convince yourself of this fact!
The magnitude of the radial acceleration is equal to the product of the radius and the square of the angular velocity.


