05.Potential Energy Functions
- Page ID
- 458
Potential Energy Functions
The potential energy functions for the work done by gravity and by springs make analyzing many situations much easier. In light of this, why don't we construct potential energy functions for the work done by every different type fo force that could possibly act on an object? Of course, one reason is that there are too many different types of forces. Having a potential energy function for the work done by every one of them would lead to so many potential energy functions that it would be hard to keep them all straight.
Another, more subtle reason is that it is impossible to construct potential energy functions for certain forces. A potential energy function must, by definition, be a funciton. Mathematically speaking, a potential energy function of position must assign a single, specific value of potential energy to every position. Functions must be single-valued. If you specify a height off of the ground, or the deformation of the spring, the potential energy function tells you exactly how much energy the system possesses at that position, regardless of the path the object took to reach that position.
In light of this observation, let's try to create a potential energy function to replace the work done by friction.
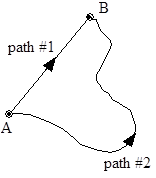
Imagine sliding an object along a rough surface from point A to point B. If you slide the object along path #1, the force of friction will do a certain amount of work on the object. (This work will be negative because the direction of the force of friction is always in opposition to the change in position of the object.)
If you slide the object along path #2, you should see that the magnitude of the work done by friction will be greater. (Although the frictional force will be the same in magnitude, the distance over which the frictional force acts will be larger. Thus, a larger amount of negative work will be done by friction.)
Now let's try to create a potential energy function for the work done by friction. Since we are always free to choose a coordinate system, we can choose a system in which the potential energy at A is zero. What is the value for the potential energy at B? Since the work done by friction depends on the path taken from A to B, so must the potential energy. However, this leaves us with a potential energy at B that can be either one of two values, depending on the path taken! Since a function must be single-valued, the work done by friction cannot be represented by a function. You can not create a potential energy function for the work done by friction!
There are also other forces whose work can not be represented by a potential energy function. In general, forces whose work can be represented by a potential energy function are termed conservative forces, while those for which potential energy functions can not be constructed are termed non-conservative.


