1.1: Reflection and Refraction
- Page ID
- 7348
Reflection of light from a smooth, shiny surface is called specular reflection. (Latin speculum a mirror.) At the other extreme we have the sort of diffuse scattering that occurs when you shine light on blotting paper. And there are lots of situations in between these extremes. In this chapter I am going to deal solely with specular reflection, the law of specular reflection being that the angle of reflection is equal to the angle of incidence.
When light passes from one medium to another, the angles of incidence and refraction, and the two refractive indices are related by the familiar Snell’s Law,
\[n_1 \sin \theta_1 = n_2 \sin \theta_2.\]
In this chapter we are going to look at the laws of reflection and refraction from the point of view of Fermat’s Principle of Least Action, and Snell’s law of refraction from the point of view of Huygens’ construction. We’ll start with the law of reflection (angle of reflection equals angle of incidence).
Light goes from A to B via reflection from a point P on a mirror.
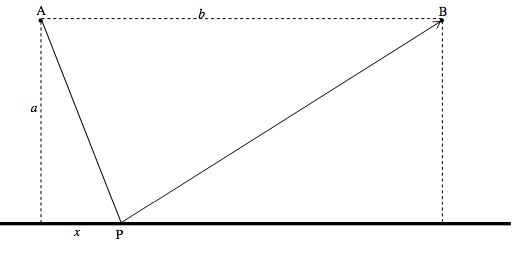
The distance \(s\) travelled is given by
\[s = \sqrt{a^2 +x^2} + \sqrt{a^2 + (b-x)^2}. \]
Here is a graph of \(s\) versus \(x\) (i.e. \(s\) as a function of the position of the point P from which the light is reflected). The drawing above is drawn for \(a = \frac{1}{2}b \), and, in the graph below, \(s\) and \(x\) are in units of b.

From the graph, or by differentiation of \(s\) with respect to \(x\) (do it!), it is seen that the path length is least when \(x = \dfrac{1}{2} b\), i.e. when the angle of reflection is equal to the angle of incidence.
Of all possible paths the light might conceivably take, the path that it actually takes is the one with the shortest path.
Now let us look at refraction at an interface.
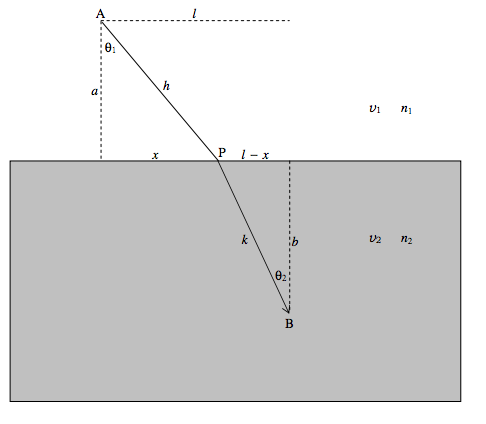
In the drawing, light is travelling from A to B, first in a medium of refractive index \(n_1\) (speed = \(v_1\)) and then in a medium of refractive index \(n_2\) (speed = \(v_2\)), via the point P.
The time taken to get from A to B is
\[t = \dfrac{\sqrt{a^2 + x^2}}{v_1}+ \dfrac{\sqrt{b^2 +(l-x)^2}}{v_2}\]
Given that \(v_1 = c / n_1\) and \( v_2 = c / n_2\), this can be written
\[ct = n_1\sqrt{a^2 + x^2} + n_2 \sqrt{b^2 + (l-x)^2}.\]
If we vary the position of P, the time taken varies as
\[c \dfrac{dt}{dx} = \dfrac{n_1x}{\sqrt{a^2 + x^2}}-\dfrac{n_2(l-x)}{\sqrt{b^2+(l-x)}^2} = n_1 \sin\theta_1 - n_2 \sin \theta_2.\]
The route actually taken is such that for any small deviation \(dx\) from the route actually taken, the corresponding variation \(dt\) in the time taken is zero. That is to say, the derivative is zero, or \(n_1 \sin \theta_1 = n_2 \sin \theta_2\).
In both cases, reflection and refraction, the route taken is such that the time taken is least. This is an example of Fermat’s Principle of Least Action. I am not sure that this is an explanation of why reflection and refraction happen the way they do as much as an interesting description of what happens in nature. A further example of the principle, from Classical Mechanics, is Hamilton’s Variational Principle. The action that a mechanical system takes in going from one state to another is \( \int Ldt\), where \(L\) is the Lagrangian at time \(t\). The route that any mechanical system takes in going from one state to another is such that any small deviation from this route results in no change in the action (which usually means that the action is a minimum). Again, I am not sure that this explains why mechanical systems behave as they do. It is more a useful description of how mechanical events unfold.
Now let us looks at Huygens’ Construction. Imagine that you are following the progress of a wavefront, and you can see the wavefront at some instant of time, and that you want to know what happens next. Huygens’ construction supposes that any point in the wavefront can be regarded as point source for a new disturbance.
For example, in the drawing below, we have wavefront moving from top to bottom.

Now we suppose that every point on the wavefront is a point source for a new disturbance:

The tangent to these little wavelets is the new wavefront:

Now let us look at refraction at an interface between two media.
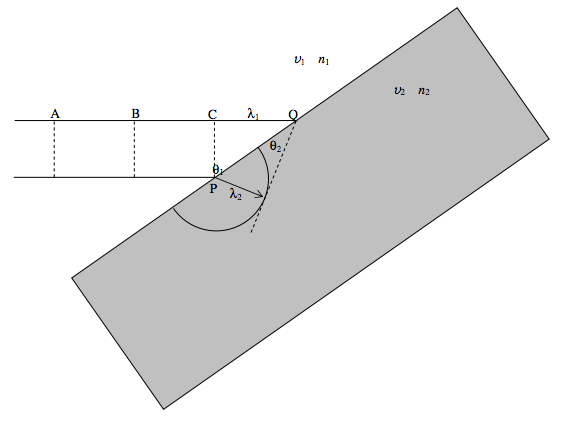
The vertical dashed lines at A, B, C represent wavefronts, separated by the wavelength \(\lambda_1\). The angle of incidence is \( \theta_1\). At some instant of time, the lower ray reaches the point P, and it starts to generate a new wavelet. At a time \(P\) later, where \(P\) is the period of the electromagnetic oscillations, the upper ray has reached the point Q, where CQ = \( \lambda_1\), while the wavelet generated at P has attained a radius \( \lambda 2\). Here \(\lambda_1\lambda_2 = v_1/v_2 = n_2/n_1\).
The new wavelet generated at Q hasn’t started yet, or at least is just about to start. The new wavefront is constructed by drawing the tangent from Q to the wavelet generated at P. From the geometry of the drawing we see that
\(\dfrac{\sin \theta_1}{\sin \theta_2}=\dfrac{\lambda_1 \text{/PQ}}{\lambda_2 \text{/PQ}}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{n_1}{n_2},\)
and so Snell’s Law is derived from the Huygens Construction. I leave it to the reader to decide whether this explains what happens, or merely describes what happens. Perhaps in science we never “explain” nature - we just “describe” it.


