7.P: Exercises

Last updated
Save as PDF

Page ID: 1225

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Calculate the energy-shift in the ground state of the one-dimensional harmonic oscillator when the perturbation 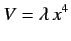$V = \lambda\,x^4$ is added to 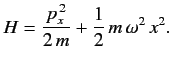$H = \frac{p_x^{\,2}}{2\,m} + \frac{1}{2}\,m\,\omega^2\,x^2.$ The properly normalized ground-state wavefunction is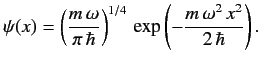 $\psi(x) = \left(\frac{m\,\omega}{\pi\,\hbar}\right)^{1/4}\,\exp\left(-\frac{m\,\omega^2\,x^2}{2\,\hbar}\right).$
Calculate the energy-shifts due to the first-order Stark effect in the $ n=3$ state of a hydrogen atom. You do not need to perform all of the integrals, but you should construct the correct linear combinations of states.
The Hamiltonian of the valence electron in a hydrogen-like atom can be written 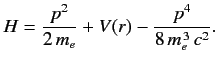$H = \frac{p^2}{2\,m_e} + V(r) - \frac{p^4}{8\,m_e^{\,3}\,c^2}.$ Here, the final term on the right-hand side is the first-order correction due to the electron's relativistic mass increase. Treating this term as a small perturbation, deduce that it causes an energy-shift in the energy eigenstate characterized by the standard quantum numbers $ n$ , $ l$ , $ m$ of 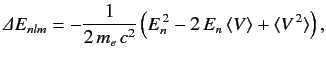${\mit\Delta}E_{nlm} = -\frac{1}{2\,m_e\,c^2}\left(E_n^{\,2} - 2\,E_n\,\langle V\rangle + \langle V^{\,2}\rangle\right),$ where $ E_n$ is the unperturbed energy, and $ \alpha$ the fine structure constant.
Consider an energy eigenstate of the hydrogen atom characterized by the standard quantum numbers $ n$ , $ l$ , and $ m$ . Show that if the energy-shift due to spin-orbit coupling (see Section 7.7) is added to that due to the electron's relativistic mass increase (see previous exercise) then the net fine structure energy-shift can be written 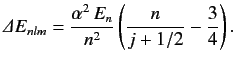${\mit\Delta} E_{nlm} = \frac{\alpha^2\,E_n}{n^2}\left(\frac{n}{j+1/2}-\frac{3}{4}\right).$ Here, $ E_n$ is the unperturbed energy, $ \alpha$ the fine structure constant, and $ j=l\pm 1/2$ the quantum number associated with the magnitude of the sum of the electron's orbital and spin angular momenta. You will need to use the following standard results for a hydrogen atom:

$ a_0$

$ l=0$

$ (2p)_{3/2}$

$ (2p)_{1/2}$

$ (2s)_{1/2}$

$ 4.5\times 10^{-5}\,{\rm eV}$

Contributors

Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

$ \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$