8.6: Sudden Perturbations
- Page ID
- 1231
Consider, for example, a constant perturbation that is suddenly switched on at time \( t=0\) :
where \( H_1\) is time-independent, but is generally a function of the position, momentum, and spin operators. Suppose that the system is definitely in state \( \vert i\rangle\) at time \( t=0\) . According to Equations \ref{795}-\ref{797} (with \( t_0=0\) ),
![$ = -\frac{{\rm i}}{\hbar}\, H_{ni} \int_0^t dt'\,\exp[\,{\rm i}\, ...
...{ni}\,(t'-t)]= \frac{H_{ni}}{E_n - E_i}\, [1- \exp(\,{\rm i}\,\omega_{ni}\,t)],$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1893.png)
giving
![$ P_{i\rightarrow n}(t) \simeq \vert c_n^{\ref{1}}\vert^{\,2} = \frac{4...
...vert E_n - E_i\vert^{\,2}}\, \sin^2\left[ \frac{(E_n-E_i)\,t}{2\,\hbar}\right],$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1894.png)
for \( i\neq n\) . The transition probability between states \( \vert i\rangle\) and \( \vert n\rangle\) can be written
where
The sinc function is highly oscillatory, and decays like \( 1/\vert x\vert\) at large \( \vert x\vert\) . It is a good approximation to say that \( {\rm sinc}(x)\) is small except when \( \vert x\vert \stackrel {_{\normalsize <}}{_{\normalsize\sim}}\pi\) . It follows that the transition probability, \( P_{i\rightarrow n}\) , is small except when
Note that in the limit \( t\rightarrow \infty\) only those transitions that conserve energy (i.e., \( E_n=E_i\) ) have an appreciable probability of occurrence. At finite \( t\) , is is possible to have transitions which do not exactly conserve energy, provided that
where \( {\mit\Delta} E = \vert E_n - E_i\vert\) is the change in energy of the system associated with the transition, and \( {\mit\Delta} t = t\) is the time elapsed since the perturbation was switched on. This result is just a manifestation of the well-known uncertainty relation for energy and time. Incidentally, the energy-time uncertainty relation is fundamentally different to the position-momentum uncertainty relation, because (in non-relativistic quantum mechanics) position and momentum are operators, whereas time is merely a parameter.
The probability of a transition that conserves energy (i.e., \( E_n=E_i\) ) is
where use has been made of \( {\rm sinc}\ref{0} = 1\) . Note that this probability grows quadratically with time. This result is somewhat surprising, because it implies that the probability of a transition occurring in a fixed time interval, \( t\) to \( t+dt\) , grows linearly with \( t\) , despite the fact that \( H_1\) is constant for \( t>0\) . In practice, there is usually a group of final states, all possessing nearly the same energy as the energy of the initial state \( \vert i\rangle\) . It is helpful to define the density of states, \( \rho(E)\) , where the number of final states lying in the energy range \( E\) to \( E+dE\) is given by \( \rho(E)\,dE\) . Thus, the probability of a transition from the initial state \( i\) to any of the continuum of possible final states is
giving
where
and use has been made of Equation \ref{805}. We know that in the limit \( t\rightarrow \infty\) the function \( {\rm sinc}(x)\) is only non-zero in an infinitesimally narrow range of final energies centered on \( E_n=E_i\) . It follows that, in this limit, we can take \( \rho(E_n)\) and \( \vert H_{ni}\vert^{\,2}\) out of the integral in the above formula to obtain
where \( P_{i\rightarrow [n]}\) denotes the transition probability between the initial state \( \vert i\rangle\) and all final states \( \vert n\rangle\) that have approximately the same energy as the initial state. Here, \( \overline{\vert H_{ni}\vert^{\,2}}\) is the average of \( \vert H_{ni}\vert^{\,2}\) over all final states with approximately the same energy as the initial state. In deriving the above formula, we have made use of the result
Note that the transition probability, \( P_{i\rightarrow [n]}\) , is now proportional to \( t\) , instead of \( t^2\) .
It is convenient to define the transition rate, which is simply the transition probability per unit time. Thus,
giving
This appealingly simple result is known as Fermi's golden rule. Note that the transition rate is constant in time (for \( t>0\) ): i.e., the probability of a transition occurring in the time interval \( t\) to \( t+dt\) is independent of \( t\) for fixed \( dt\) . Fermi's golden rule is sometimes written
where it is understood that this formula must be integrated with \( \int dE_n\,\rho(E_n)\) to obtain the actual transition rate.
Let us now calculate the second-order term in the Dyson series, using the constant perturbation \ref{801}. From Equation \ref{797} we find that
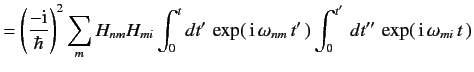
![$ =\frac{\rm i}{\hbar} \sum_m \frac{H_{nm} \,H_{mi}}{E_m - E_i} \in...
...[\exp(\,{\rm i}\,\omega_{ni}\,t'\,) - \exp(\,{\rm i}\,\omega_{nm}\,t']\,\right)$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1931.png)
![$ = \frac{{\rm i}\,t}{\hbar} \sum_m \frac{H_{nm} H_{mi}}{E_m - E_i}...
...t/2)- \exp(\,{\rm i}\,\omega_{nm} \,t/2) \,{\rm sinc}(\omega_{nm}\,t/2)\right].$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1932.png)
Thus,
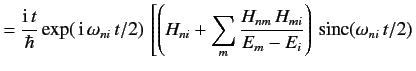
where use has been made of Equation \ref{803}. It follows, by analogy with the previous analysis, that
![$ w_{i\rightarrow [n]} =\left. \frac{2\pi}{\hbar}\, \overline{ \lef...
...\,H_{mi}}{E_m - E_i}\right\vert^{\,2}} \rho(E_n) \right\vert _{E_n \simeq E_i},$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1936.png)
where the transition rate is calculated for all final states, \( \vert n\rangle\) , with approximately the same energy as the initial state, \( \vert i\rangle\) , and for intermediate states, \( \vert m\rangle\) whose energies differ from that of the initial state. The fact that \( E_m\neq E_i\) causes the last term on the right-hand side of Equation \ref{819} to average to zero (due to the oscillatory phase-factor) during the evaluation of the transition probability.
According to Equation \ref{820}, a second-order transition takes place in two steps. First, the system makes a non-energy-conserving transition to some intermediate state \( \vert m\rangle\) . Subsequently, the system makes another non-energy-conserving transition to the final state \( \vert n\rangle\) . The net transition, from \( \vert i\rangle\) to \( \vert n\rangle\) , conserves energy. The non-energy-conserving transitions are generally termed virtual transitions, whereas the energy conserving first-order transition is termed a real transition. The above formula clearly breaks down if \( H_{nm}\,H_{mi}\neq 0\) when \( E_m = E_i\) . This problem can be avoided by gradually turning on the perturbation: i.e., ![]() (where \( \eta\) is very small). The net result is to change the energy denominator in Equation \ref{820} from \( E_i-E_m\) to
(where \( \eta\) is very small). The net result is to change the energy denominator in Equation \ref{820} from \( E_i-E_m\) to 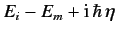 .
.
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


