8.P: Exercises
- Page ID
- 1237
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Demonstrate that \( {\bf p}\cdot{\bf A}={\bf A}\cdot{\bf p}\) when \( \nabla\cdot{\bf A} = 0\) , where \( {\bf p}\) is the momentum operator, and \( {\bf A}({\bf x})\) is a real function of the position operator, \( {\bf x}\) . Hence, show that the Hamiltonian \ref{870} is Hermitian.
- Find the selection rules for the matrix elements \( \langle n,l,m\vert\,x\,\vert n',l',m'\rangle\) , \( \langle n,l,m\vert\,y\,\vert n',l',m'\rangle\) , and \( \langle n,l, m\vert\,z\,\vert n',l',m'\rangle\) to be non-zero. Here, \( \vert n,l,m\rangle\) denotes an energy eigenket of a hydrogen-like atom corresponding to the conventional quantum numbers, \( n\) , \( l\) , and \( m\) .
- Demonstrate that \( \left\langle \vert\mbox{\boldmath\) where the average is taken over all directions of the incident radiation.
- Demonstrate that the spontaneous decay rate (via an electric dipole transition) from any 2p state to a 1s state of a hydrogen atom is
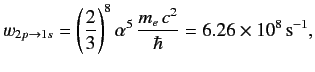 where \( \alpha\) is the fine structure constant. Hence, deduce that the natural line width of the associated spectral line is
where \( \alpha\) is the fine structure constant. Hence, deduce that the natural line width of the associated spectral line is 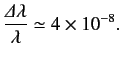 The only non-zero \( 1s\leftrightarrow 2p\) electric dipole matrix elements take the values
The only non-zero \( 1s\leftrightarrow 2p\) electric dipole matrix elements take the values
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


