9.P: Exercises

Last updated
Save as PDF

Page ID: 1247

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Consider a scattering potential of the form 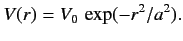$V(r)=V_0\,\exp(-r^2/a^2).$ Calculate the differential scattering cross-section, $ V_0$ for $ r<R$ , and is zero for $ r>R$ , where $ \vert V_0\vert\ll E=\hbar^2\,k^2/2\,m$ , and $ k\,R\ll 1$ , the differential cross-section is isotropic, and that the total cross-section is 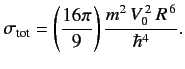$\sigma_{\rm tot} = \left(\frac{16\pi}{9}\right) \frac{m^2\,V_0^{\,2}\,R^{\,6}}{\hbar^4}.$ Suppose that the energy is slightly raised. Show that the angular distribution can then be written in the form 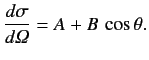$\frac{d\sigma}{d{\mit\Omega} }= A + B\,\cos\theta.$ Obtain an approximate expression for $ \delta$ -shell potential: 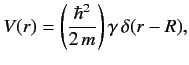$V(r) = \left(\frac{\hbar^2}{2\,m}\right)\gamma\,\delta(r-R),$ where $ s$ -wave phase-shift, $ k$ (where $ \gamma\gg R^{-1}$ , $ \tan(k\,R)$ is not close to zero then the $ \tan(k\,R)$ is close to zero then resonance behavior is possible: i.e., $ k$ increases. Determine the approximate positions of the resonances (retaining terms up to order $ R$ . Obtain an approximate expression for the resonance width ${\mit\Gamma} = - \frac{2}{[d(\cot\delta_0)/dE]_{E=E_r}}.$ Show that the resonances become extremely sharp as $ \gamma\rightarrow \infty$ .
Show that the differential cross-section for the elastic scattering of a fast electron by the ground-state of a hydrogen atom is $\frac{d\sigma}{d{\mit\Omega}} = \left(\frac{2\,m_e\,e^2}{4\pi\,\e... ...n_0\,\hbar^{\,2}\,q^2}\right)^2\left(1-\frac{16}{[4+(q\,a_0)^2]^{\,2}}\right),$ where $ a_0$ is the Bohr radius.

Contributors

Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

$ \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$