2.7: Experimental Tests of Lorentz Geometry
- Page ID
- 10457
We’ve already seen, in section 1.2, a variety of evidence for the nonclassical behavior of spacetime. We’re now in a position to discuss tests of relativity more quantitatively. An up-to-date review of such tests is given by Mattingly.14
One such test is that relativity requires the speed of light to be the same in all frames of reference, for the following reasons. Compare with the speed of sound in air. The speed of sound is not the same in all frames of reference, because the wave propagates at a fixed speed relative to the air. An observer at who is moving relative to the air will measure a different speed of sound. Light, on the other hand, isn’t a vibration of any physical medium. Maxwell’s equations predict a definite value for the speed of light, regardless of the motion of the source. This speed also can’t be relative to any medium. If the speed of light isn’t fixed relative to the source, and isn’t fixed relative to a medium, then it must be fixed relative to anything at all. The only speed in relativity that is equal in all frames of reference is c, so light must propagate at c. We will see later that there is a deeper reason for this; relativity requires that any massless particle propagate at c. The requirement of v = c for massless particles is so intimately hard-wired into the structure of relativity that any violation of it, no matter how tiny, would be of great interest. Essentially, such a violation would disprove Lorentz invariance, i.e., the invariance of the laws of physics under Lorentz transformations. There are two types of tests we could do: (1) test whether photons of all energies travel at the same speed, i.e., whether the vacuum is dispersive; (2) test whether observers in all frames of reference measure the same speed of light.
Dispersion of the Vacuum
Some candidate quantum-mechanical theories of gravity, such as loop quantum gravity, predict a granular structure for spacetime at the Planck scale, \(\sqrt{\frac{\hbar G}{c^{3}}}\) = 10−35 m, which one could imagine might lead to deviations from v = 1 that would become more and more significant for photons with wavelengths getting closer and closer to that scale. Lorentz-invariance would then be an approximation valid only at large scales. It turns out that the state of the art in loop quantum gravity is not yet sufficient to say whether or not such an effect should exist.
Presently the best experimental tests of the invariance of the speed of light with respect to wavelength come from astronomical observations of gamma-ray bursts, which are sudden outpourings of high-energy photons, believed to originate from a supernova explosion in another galaxy. One such observation, in 2009,15 collected photons from such a burst, with a duration of 2 seconds, indicating that the propagation time of all the photons differed by no more than 2 seconds out of a total time in flight on the order of ten billion years, or about one part in 1017! A single superlative photon in the burst had an energy of 31 GeV, and its arrival within the same 2-second time window demonstrates Lorentz invariance over a vast range of photon energies, contradicting heuristic estimates that had been made by some researchers in loop quantum gravity.

Observer-independence of c
The constancy of the speed of light for observers in all frames of reference was originally detected in 1887 when Michelson and Morley set up a clever apparatus to measure any difference in the speed of light beams traveling east-west and north-south. The motion of the earth around the sun at 110,000 km/hour (about 0.01% of the speed of light) is to our west during the day. Michelson and Morley believed that light was a vibration of a physical medium, the ether, so they expected that the speed of light would be a fixed value relative to the ether. As the earth moved through the ether, they thought they would observe an effect on the velocity of light along an east-west line. For instance, if they released a beam of light in a westward direction during the day, they expected that it would move away from them at less than the normal speed because the earth was chasing it through the ether. They were surprised when they found that the expected 0.01% change in the speed of light did not occur.
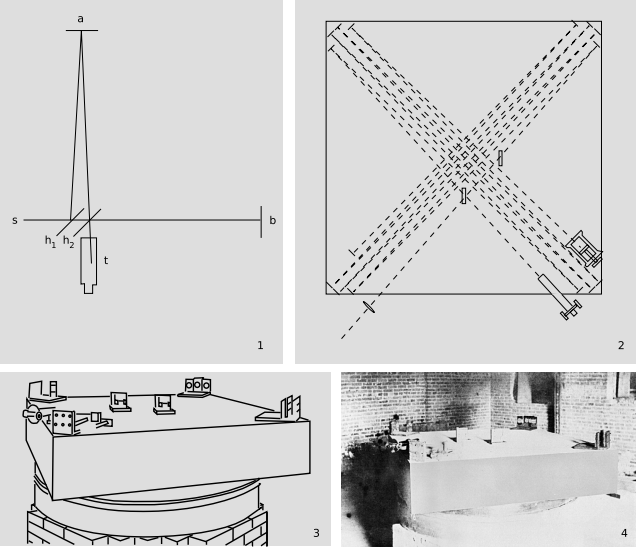
Although the Michelson-Morley experiment was nearly two decades in the past by the time Einstein published his first paper on relativity in 1905, and Einstein did know about it,16 it’s unclear how much it influenced him. Michelson and Morley themselves were uncertain about whether the result was to be trusted, or whether systematic and random errors were masking a real effect from the ether. There were a variety of competing theories, each of which could claim some support from the shaky data. Some physicists believed that the ether could be dragged along by matter moving through it, which inspired variations on the experiment that were conducted on mountaintops in thin-walled buildings, (figure), or with one arm of the apparatus out in the open, and the other surrounded by massive lead walls. In the standard sanitized textbook version of the history of science, every scientist does his experiments without any preconceived notions about the truth, and any disagreement is quickly settled by a definitive experiment. In reality, this period of confusion about the Michelson-Morley experiment lasted for four decades, and a few reputable skeptics, including Miller, continued to believe that Einstein was wrong, and kept trying different variations of the experiment as late as the 1920’s. Most of the remaining doubters were convinced by an extremely precise version of the experiment performed by Joos in 1930, although you can still find kooks on the internet who insist that Miller was right, and that there was a vast conspiracy to cover up his results.


Before Einstein, some physicists who did believe the negative result of the Michelson-Morley experiment came up with explanations that preserved the ether. In the period from 1889 to 1895, both Lorentz and George FitzGerald suggested that the negative result of the Michelson-Morley experiment could be explained if the earth, and every physical object on its surface, was contracted slightly by the strain of the earth’s motion through the ether. Thus although Lorentz developed all the mathematics of Lorentz frames, and got them named after himself, he got the interpretation wrong.
Lorentz Violation by Gravitational Forces
The tests described in earlier both involve the behavior of light, i.e., they test whether or not electromagnetism really has the exact Lorentz-invariant behavior contained implicitly in Maxwell’s equations. In the jargon of the field, they test Lorentz invariance in the “photon sector.” Since relativity is a theory of gravity, it is natural to ask whether the Lorentz invariance holds for gravitational forces as well as electromagnetic ones. If Lorentz invariance is violated by gravity, then the strength of gravitational forces might depend on the observer’s motion through space, relative to some fixed reference frame analogous to that of the ether. Historically, gravitational Lorentz violations have been much more difficult to test, since gravitational forces are so weak, and the first high-precision data were obtained by Nordtvedt and Will in 1957, 70 years after Michelson and Morley. Nordtvedt and Will measured the strength of the earth’s gravitational field as a function of time, and found that it did not vary on a 24-hour cycle with the earth’s rotation, once tidal effects had been accounted for. Further constraints come from data on the moon’s orbit obtained by reflecting laser beams from a mirror left behind by the Apollo astronauts.
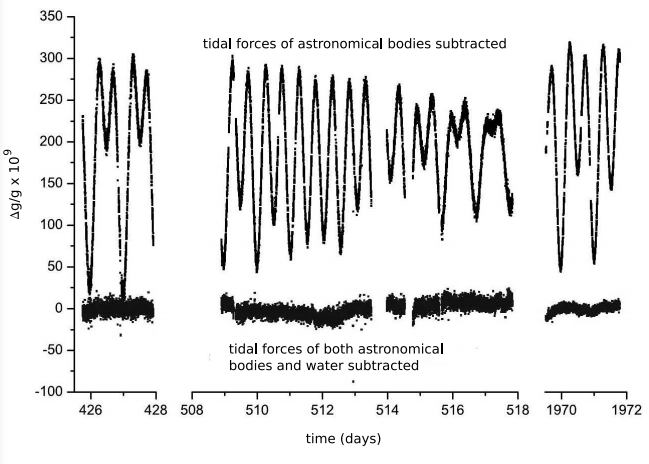
A recent high-precision laboratory experiment was done in 2009 by Chung et al.17 They constructed an interferometer in a vertical plane that is conceptually similar to a Michelson interferometer, except that it uses cesium atoms rather than photons. That is, the light waves of the Michelson-Morley experiment are replaced by quantum-mechanical matter waves. The roles of the half-silvered and fully silvered mirrors are filled by lasers, which kick the atoms electromagnetically. Each atom’s wavefunction is split into two parts, which travel by two different paths through spacetime, eventually reuniting and interfering. The result is a measurement of g to about one part per billion. The results, shown in figure d, put a strict limit on violations of Lorentz geometry by gravity.
References
14 livingreviews.org/lrr-2005-5
15 http://arxiv.org/abs/0908.1832
16 J. van Dongen, http://arxiv.org/abs/0908.1545
17 arxiv.org/abs/0905.1929


