4.3: Four-vectors (Part 2)
- Page ID
- 10421
The Frequency Vector and the Relativistic Doppler Shift
In the spirit of index-gymnastics notation, frequency is to time as the wavenumber k = \(\frac{1}{\lambda}\) is to space, so when treating waves relativistically it is natural to conjecture that there is a four-frequency fa made by assembling (f, k), which behaves as a Lorentz vector. This is correct, since we already know that \(\partial_{a}\) transforms as a covariant vector, and for a scalar wave of the form
\[A = A_o \exp [2\pi if_ax^a]\]
the partial derivative operator is identical to multiplication by 2\(\pi\)fa.
As an application, consider the relativistic Doppler shift of a light wave. For simpicity, let’s restrict ourselves to one spatial dimension. For a light wave, \(f = k\), so the frequency vector in 1+1 dimensions is simply (f, f). Putting this through a Lorentz transformation, we find
\[f' = (1 + v) \gamma f = \sqrt{\frac{1+v}{1-v}} f,\]
where the second form displays more clearly the symmetic form of the relativistic relationship, such that interchanging the roles of source and observer is equivalent to flipping the sign of v. That is, the relativistic version only depends on the relative motion of the source and the observer, whereas the Newtonian one also depends on the source’s motion relative to the medium (i.e., relative to the preferred frame in which the waves have the “right” velocity). In Newtonian mechanics, we have f' = (1 + v)f for a moving observer. Relativistically, there is also a time dilation of the oscillation of the source, providing an additional factor of \(\gamma\).
This analysis is extended to 3+1 dimensions in problem 11.
Example 15: Ives-Stilwell experiments
The relativistic Doppler shift differs from the nonrelativistic one by the time-dilation factor \(\gamma\), so that there is still a shift even when the relative motion of the source and the observer is perpendicular to the direction of propagation. This is called the transverse Doppler shift. Einstein suggested this early on as a test of relativity. However, such experiments are difficult to carry out with high precision, because they are sensitive to any error in the alignment of the 90-degree angle. Such experiments were eventually performed, with results that confirmed relativity,7 but one-dimensional measurements provided both the earliest tests of the relativistic Doppler shift and the most precise ones to date. The first such test was done by Ives and Stilwell in 1938, using the following trick. The relativistic expression
\[S_{v} = \sqrt{\frac{(1 + v)}{(1 − v)}}\]
for the Doppler shift has the property that
\[S_vS_{−v} = 1\]
which differs from the nonrelativistic result of
\[(1 + v)(1 − v) = 1 − v^2.\]
One can therefore accelerate an ion up to a relativistic speed, measure both the forward Doppler shifted frequency ff and the backward one fb, and compute \(\sqrt{f_{f} f_{b}}\). According to relativity, this should exactly equal the frequency fo measured in the ion’s rest frame.
In a particularly exquisite modern version of the Ives-Stilwell idea,8 Saathoff et al. circulated Li+ ions at v = .064 in a storage ring. An electron-cooler technique was used in order to reduce the variation in velocity among ions in the beam. Since the identity SvS−v = 1 is independent of v, it was not necessary to measure v to the same incredible precision as the frequencies; it was only necessary that it be stable and well-defined. The natural line width was 7 MHz, and other experimental effects broadened it further to 11 MHz. By curve-fitting the line, it was possible to achieve results good to a few tenths of a MHz. The resulting frequencies, in units of MHz, were:
ff = 582490203.44 ± .09
fb = 512671442.9 ± 0.5
\(\sqrt{f_{f} f_{b}}\) = 546466918.6 ± 0.3
fo = 546466918.8 ± 0.4 (from previous experimental work)
The spectacular agreement with theory has made this experiment a lightning rod for anti-relativity kooks.
If one is searching for small deviations from the predictions of special relativity, a natural place to look is at high velocities. IvesStilwell experiments have been performed at velocities as high as 0.84, and they confirm special relativity.9
7 See, e.g., Hasselkamp, Mondry, and Scharmann, Zeitschrift f¨ur Physik A: Hadrons and Nuclei 289 (1979) 151.
8 G. Saathoff et al., “Improved Test of Time Dilation in Relativity,” Phys. Rev. Lett. 91 (2003) 190403. A publicly available description of the experiment is given in Saathoff’s PhD thesis, www.mpi-hd.mpg.de/ato/homes/saathoff/ diss-saathoff.pdf.
9 MacArthur et al., Phys. Rev. Lett. 56 (1986) 282 (1986)
2
Earlier, we showed that the celebrated E = mc2 follows directly from the form of the Lorentz transformation. An alternative derivation was given by Einstein in one of his classic 1905 papers laying out the theory of special relativity; the paper is short, and is reproduced in English translation in Appendix A of this book. Having laid the groundwork of four-vectors and relativistic Doppler shifts, we can give an even shorter version of Einstein’s argument. The discussion is also streamlined by restricting the discussion to 1+1 dimensions and by invoking photons.
Suppose that a lantern, at rest in the lab frame, is floating weightlessly in outer space, and simultaneously emits two pulses of light in opposite directions, each with energy \(\frac{E}{2}\) and frequency f. By symmetry, the momentum of the pulses cancels, and the lantern remains at rest. An observer in motion at velocity v relative to the lab sees the frequencies of the beams shifted to f' = (1 ± v)\(\gamma\)f. The effect on the energies of the beams can be found purely classically, by transforming the electric and magnetic fields to the moving frame, but as a shortcut we can apply the quantum-mechanical relation Eph = hf for the energies of the photons making up the beams. The result is that the moving observer finds the total energy of the beams to be not E but (\(\frac{E}{2}\))(1 + v)\(\gamma\) + (\(\frac{E}{2}\))(1 − v)\(\gamma\) = E\(\gamma\).
Both observers agree that the lantern had to use up some of the energy stored in its fuel in order to make the two pulses. But the moving observer says that in addition to this energy E, there was a further energy E(\(\gamma\) − 1). Where could this energy have come from? It must have come from the kinetic energy of the lantern. The lantern’s velocity remained constant throughout the experiment, so this decrease in kinetic energy seen by the moving observer must have come from a decrease in the lantern’s inertial mass — hence the title of Einstein’s paper, “Does the inertia of a body depend upon its energy content?”
To figure out how much mass the lantern has lost, we have to decide how we can even define mass in this new context. In Newtonian mechanics, we had K = (\(\frac{1}{2}\))mv2, and by the correspondence principle this must still hold in the low-velocity limit. Expanding E(\(\gamma\) − 1) in a Taylor series, we find that it equals E(\(\frac{v^{2}}{2}\)) + . . ., and in the low-velocity limit this must be the same as \(\Delta K = (\frac{1}{2}) \Delta mv^{2}\), so \(\Delta\)m = E. Reinserting factors of c to get back to nonrelativistic units, we have E = \(\Delta\)mc2.
A Non-example: Electric and Magnetic Fields
It is fairly easy to see that the electric and magnetic fields cannot be the spacelike parts of two four-vectors. Consider the arrangement shown in Figure 4.2.2 (1). We have two infinite trains of moving charges superimposed on the same line, and a single charge alongside the line. Even though the line charges formed by the two trains are moving in opposite directions, their currents don’t cancel. A negative charge moving to the left makes a current that goes to the right, so in frame 1, the total current is twice that contributed by either line charge.
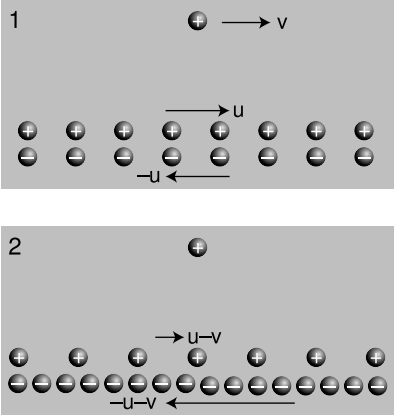
In frame 1 the charge densities of the two line charges cancel out, and the electric field experienced by the lone charge is therefore zero. Frame 2 shows what we’d see if we were observing all this from a frame of reference moving along with the lone charge. Both line charges are in motion in both frames of reference, but in frame 1, the line charges were moving at equal speeds, so their Lorentz contractions were equal, and their charge densities canceled out. In frame 2, however, their speeds are unequal. The positive charges are moving more slowly than in frame 1, so in frame 2 they are less contracted. The negative charges are moving more quickly, so their contraction is greater now. Since the charge densities don’t cancel, there is an electric field in frame 2, which points into the wire, attracting the lone charge.
We appear to have a logical contradiction here, because an observer in frame 2 predicts that the charge will collide with the wire, whereas in frame 1 it looks as though it should move with constant velocity parallel to the wire. Experiments show that the charge does collide with the wire, so to maintain the Lorentz-invariance of electromagnetism, we are forced to invent a new kind of interaction, one between moving charges and other moving charges, which causes the acceleration in frame 2. This is the magnetic interaction, and if we hadn’t known about it already, we would have been forced to invent it. That is, magnetism is a purely relativistic effect. The reason a relativistic effect can be strong enough to stick a magnet to a refrigerator is that it breaks the delicate cancellation of the extremely large electrical interactions between electrically neutral objects.
Although the example shows that the electric and magnetic fields do transform when we change from one frame to another, it is easy to show that they do not transform as the spacelike parts of a relativistic four-vector. This is because transformation between frames 1 and 2 is along the axis parallel to the wire, but it affects the components of the fields perpendicular to the wire. The electromagnetic field actually transforms as a rank-2 tensor.
The Electromagnetic Potential Four-vector
An electromagnetic quantity that does transform as a four-vector is the potential. In section 3.7, I mentioned the fact, which may or may not already be familiar to you, that whereas the Newtonian gravitational field’s polarization properties allow it to be described using a single scalar potential \(\phi\) or a single vector field \(\textbf{g} = − \nabla \phi\), the pair of electromagnetic fields (E, B) needs a pair of potentials, \(\boldsymbol{\Phi}\) and A. It’s easy to see that \(\boldsymbol{\Phi}\) can’t be a Lorentz scalar. Electric charge q is a scalar, so if \(\boldsymbol{\Phi}\) were a scalar as well, then the product q\(\boldsymbol{\Phi}\) would be a scalar. But this is equal to the energy of the charged particle, which is only the timelike component of the energy-momentum four-vector, and therefore not a Lorentz scaler itself. This is a contradiction, so \(\boldsymbol{\Phi}\) is not a scalar.
To see how to fit \(\boldsymbol{\Phi}\) into relativity, consider the nonrelativistic quantum mechanical relation q\(\boldsymbol{\Phi}\) = hf for a charged particle in a potential \(\boldsymbol{\Phi}\). Since f is the timelike component of a four-vector in relativity, we need \(\boldsymbol{\Phi}\) to be the timelike component of some four vector, Ab. For the spacelike part of this four-vector, let’s write A, so that \(A_{b} = (\boldsymbol{\Phi}, \textbf{A})\). We can see by the following argument that this mysterious A must have something to do with the magnetic field.
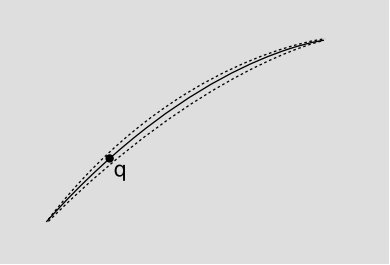
Consider the example of Figure 4.2.3 from a quantum-mechanical point of view. The charged particle q has wave properties, but let’s say that it can be well approximated in this example as following a specific trajectory. This is like the ray approximation to wave optics. A light ray in classical optics follows Fermat’s principle, also known as the principle of least time, which states that the ray’s path from point A to point B is one that extremizes the optical path length (essentially the number of oscillations). The reason for this is that the ray approximation is only an approximation. The ray actually has some width, which we can visualize as a bundle of neighboring trajectories. Only if the trajectory follows Fermat’s principle will the interference among the neighboring paths be constructive. The classical optical path length is found by integrating k · ds, where k is the wavenumber. To make this relativistic, we need to use the frequency four-vector to form fb dxb, which can also be expressed as fbvb d\(\tau\) = \(\gamma\)(f − k · v) d\(\tau\). If the charge is at rest and there are no magnetic fields, then the quantity in parentheses is \(f = \frac{E}{h} = (\frac{q}{h}) \Phi\). The correct relativistic generalization is clearly fb = (\(\frac{q}{h}\))Ab.
Since Ab’s spacelike part, A, results in the velocity-dependent effects, we conclude that A is a kind of potential that relates to the magnetic field, in the same way that the potential \(\boldsymbol{\Phi}\) relates to the electric field. A is known as the vector potential, and the relation between the potentials and the fields is
\[\begin{split} \textbf{E} &= - \nabla \Phi - \frac{\partial \textbf{A}}{\partial t} \\ \textbf{B} &= \nabla \textbf{A} \ldotp \end{split}\]
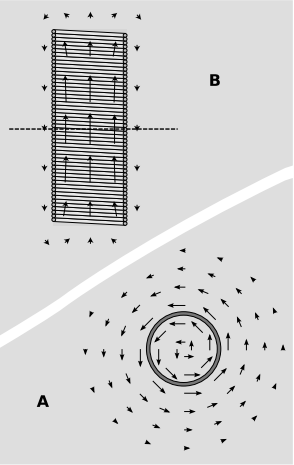
An excellent discussion of the vector potential from a purely classical point of view is given in the classic Feynman Lectures.10 Figure 4.2.4 shows an example.
References
10 The Feynman Lectures on Physics, Feynman, Leighton, and Sands, Addison Wesley Longman, 1970


