1.5: Triangle and Cauchy-Schwarz Inequalities
- Page ID
- 3421
Learning Objectives
- Discuss the triangle and Cauchy-Schwarz
In Euclidean geometry, we have the intuitively obvious fact that any side of a triangle is no greater than the sum of the other two sides. This can be written in terms of vectors as \(|m + n| \leq |m| + |n|\). Closely related to it is the inequality \(|m \cdot n| ≤ |m| |n|\), known as the Cauchy-Schwarz inequality, which can be seen because \(m \cdot n = |m| |n| cos\theta\), where \(\theta\) is the angle between the two vectors.
Any proof of these facts ultimately depends on the assumption that the metric has the Euclidean signature \(+ + +\) (or on equivalent assumptions such as Euclid’s axioms). Figure \(\PageIndex{1}\) shows that on physical grounds, we do not expect the inequalities to hold for Minkowski vectors in their unmodified Euclidean forms. The quantity |m + n| represents the proper time of the spaceship that moved inertially along with the earth, while \(|m| + |n|\) is the greater proper time of the traveling spaceship.
On the other hand, Minkowski space has copies of Euclidean space built in. For example, we know that all the familiar Euclidean facts must hold in any plane of simultaneity defined by a particular observer at a given moment in time, since the restriction of the metric to that plane has signature \(---\), and the distinction between this and the \(+ + +\) signature is an arbitrary notational convention. Summarizing these observations, we expect that the relativistic version of the triangle and Cauchy-Schwarz inequalities will be split into cases, some of which are the same as the Euclidean case and some of them different.
Some notational issues may be confusing in the following discusion. We let \(a^2\) mean \(a \cdot a\), which may not be positive, while \(|a|\) indicates the positive real number \(\mid a \cdot a\mid\). I will try to specifically point out any equations that are only true for \(+---\) signature and not for \(- + ++\), and express important final results in a way that doesn’t depend on this choice.
Two timelike vectors
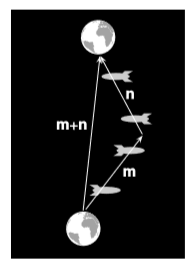
A simple and important case is the one in which both \(m\) and \(n\) trace possible world-lines of material objects, as in figure \(\PageIndex{1}\). That is, they must both be timelike vectors. To see what form of the Cauchy-Schwarz inequality should hold, we break the vector \(n\) down into two parts, \(n = n_{\parallel} + n_{\perp}\), where \(n_{\parallel}\) is parallel to \(m\) and \(n_{\perp}\) perpendicular. We then have \(|m · n| = |m · n_{\parallel} | = |m| |n_{\parallel} |\). But \(n^2 = (n_{\parallel} + n_{perp} )^2 = n_{\parallel}^2 + 2n_{\parallel} \cdot n_{\perp} + n_{\perp} = n_{\parallel}^2 + n_{\perp}^2\), and since \(n_{\parallel}\) is timelike and \(n_{\perp}\) spacelike, we have (in the \(+---\) signature) \(n_{\parallel}^2 > 0\) and \(n_{\perp}^2 < 0\). Therefore, regardless of signature, \(\lvert n\lvert ≤ \lvert n_{\parallel}\lvert\), and we have the reversed Cauchy-Schwarz inequality
\[|m \cdot n| \geq |m| |n| \quad \text{(valid for either + − −− or − + ++)}\]
A useful way of interpreting the reversal compared to the Euclidean case is that if the vectors happen to be normalized such that \(|m| = |n| = 1\), then \(m \cdot n = \gamma\), where \(\gamma\) is the Lorentz factor for an observer whose world-line is parallel to \(m\) with respect to a world- line parallel to \(n\). The difference from the Euclidean behavior can then be understood as arising from the fact that whereas \(|cos\theta| ≤ 1\), we always have \(\gamma \geq 1\).
Given the physical motivation presented so far, it would have been natural to take both \(m\) and \(n\) to lie in the future rather than the past light cone, but we have not yet assumed that this was the case, and the reversed Cauchy-Schwarz inequality holds independently of such an assumption. (See problem Q16 for an alternative way of seeing this.) In order to discuss the related triangle inequality, however, we will need to assume that both vectors are future-directed. Physically, this is necessary in order to give the interpretation shown in figure ai, from which we have already inferred that the triangle inequality must be reversed. To verify this mathematically, we can compute the difference \((m + n)^2 − (|m| + |n|)^2\) (problem 17).
Two spacelike vectors not spanning the light cone
Now suppose that \(m\) and \(n\) are both spacelike, and the plane that they span does not include the light-cone. Operating within this plane, we never get any timelike or lightlike vectors, and therefore the non-Euclidean nature of the metric is never apparent to us. The geometry of this plane is therefore Euclidean, so in this case the ordinary Euclidean versions of the Cauchy-Schwarz and triangle inequalities must hold.
Example \(\PageIndex{1}\): No relativity required
Suppose that a certain observer establishes Minkowski coordi- nates, and consider the unit vectors \(\hat{x}\) and \(\hat{y}\) lying along the \(x\) and \(y\) axes. The \(x-y\) plane that they span does not include the light cone. By plugging in to the Minkowski-coordinate form of the metric, we find that \(\hat{x} \cdot \hat{y} = 0\), as expected since the geometry of the \(x-y\) plane is Euclidean. This satisfies the ordinary form of the Cauchy-Schwarz inequality.
Two spacelike vectors spanning the light cone
Now consider the case, in Minkowski coordinates, where \(m = (0, 5, 0, 0)\) and \(n = (4, 5, 0, 0)\). These vectors span the \(t-x\) plane, whose geometry is not Euclidean, and they do not satisfy the Euclidean Cauchy-Schwarz inequality, since \(m \cdot n = -25\), whereas \(|m| |n| = 15\). Two vectors of this type will always satisfy the reversed version of the Cauchy-Schwarz inequality (problem Q18). The converse holds in the sense that if two spacelike vectors satisfy the strict inequality \(|m \cdot n| > |m| |n|\), then they span the light cone.


