5.10: Relativistic Energy
- Page ID
- 4906
By the end of this section, you will be able to:
- Explain how the work-energy theorem leads to an expression for the relativistic kinetic energy of an object
- Show how the relativistic energy relates to the classical kinetic energy, and sets a limit on the speed of any object with mass
- Describe how the total energy of a particle is related to its mass and velocity
- Explain how relativity relates to energy-mass equivalence, and some of the practical implications of energy-mass equivalence
The tokamak in Figure \(\PageIndex{1}\) is a form of experimental fusion reactor, which can change mass to energy. Nuclear reactors are proof of the relationship between energy and matter.

Conservation of energy is one of the most important laws in physics. Not only does energy have many important forms, but each form can be converted to any other. We know that classically, the total amount of energy in a system remains constant. Relativistically, energy is still conserved, but energy-mass equivalence must now be taken into account, for example, in the reactions that occur within a nuclear reactor. Relativistic energy is intentionally defined so that it is conserved in all inertial frames, just as is the case for relativistic momentum. As a consequence, several fundamental quantities are related in ways not known in classical physics. All of these relationships have been verified by experimental results and have fundamental consequences. The altered definition of energy contains some of the most fundamental and spectacular new insights into nature in recent history.
Kinetic Energy and the Ultimate Speed Limit
The first postulate of relativity states that the laws of physics are the same in all inertial frames. Einstein showed that the law of conservation of energy of a particle is valid relativistically, but for energy expressed in terms of velocity and mass in a way consistent with relativity. Consider first the relativistic expression for the kinetic energy. We again use \(u\) for velocity to distinguish it from relative velocity \(v\) between observers. Classically, kinetic energy is related to mass and speed by the familiar expression
\[K = \dfrac{1}{2} mu^2. \nonumber \]
The corresponding relativistic expression for kinetic energy can be obtained from the work-energy theorem. This theorem states that the net work on a system goes into kinetic energy. Specifically, if a force, expressed as
\[\vec{F} = \dfrac{d\vec{p}}{dt} = m\dfrac{d(\gamma \vec{u})}{dt} \nonumber \]
accelerates a particle from rest to its final velocity, the work done on the particle should be equal to its final kinetic energy. In mathematical form, for one-dimensional motion:
\[\begin{align*} K &= \int Fdx = \int m \dfrac{d}{dt} (\gamma u) dx \nonumber \\[4pt] &= m \int \dfrac{d(\gamma u)}{dt} \dfrac{dx}{dt} \\[4pt] &= m \int u \dfrac{d}{dt} \left( \dfrac{u}{\sqrt{1 - (u/c)^2}}\right) dt. \end{align*} \nonumber \]
Integrate this by parts to obtain
\[\begin{align*} K &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}}\right|_{0}^{u} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}\dfrac{du}{dt}dt \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}du \\[4pt] &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - mc^2 (\sqrt{1 - (u/c)^2})\right|_0^u \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} + \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m c^2 \\[4pt] &= mc^2 \left[ \dfrac{(u^2/c^2) + 1 - (u^2/c^2)}{\sqrt{1 - (u/c)^2}}\right] - mc^2 \nonumber \\[4pt] &= \dfrac{mc^2}{\sqrt{1 - (u/c)^2}} - mc^2. \end{align*} \nonumber \]
Therefore, the relativistic kinetic energy of any particle of mass \(m\) is
\[K_{rel} = (\gamma - 1)mc^2. \label{RKE} \]
When an object is motionless, its speed is \(u = 0\) and
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} = 1 \nonumber \]
so that \(K_{rel} = 0\) at rest, as expected. However, the expression for relativistic kinetic energy (such as total energy and rest energy) does not look much like the classical \(\dfrac{1}{2} mu^2\). To show that the expression for \(K_{rel}\) reduces to the classical expression for kinetic energy at low speeds, we use the binomial expansion to obtain an approximation for \((1 + ε)^n\) valid for small \(ε\):
\[(1 + ε)^n = 1 + nε + \dfrac{n(n−1)}{2!}ε^2 + \dfrac{n(n−1)(n−2)}{3!}ε^3 +⋯ ≈ 1 + nε \nonumber \]
by neglecting the very small terms in \(ε^2\)and higher powers of \(ε\). Choosing \(ε = −u^2/c^2\) and \(n = -\dfrac{1}{2}\) leads to the conclusion that \(\gamma\) at nonrelativistic speeds, where \(ε = u/c\) is small, satisfies
\[\gamma = (1 - u^2/c^2)^{-1/2} \approx 1 + \dfrac{1}{2} \left( \dfrac{u^2}{c^2}\right). \nonumber \]
A binomial expansion is a way of expressing an algebraic quantity as a sum of an infinite series of terms. In some cases, as in the limit of small speed here, most terms are very small. Thus, the expression derived here for \(\gamma\) is not exact, but it is a very accurate approximation. Therefore, at low speed:
\[\gamma - 1 \approx \dfrac{1}{2} \left(\dfrac{u^2}{c^2}\right). \nonumber \]
Entering this into the expression for relativistic kinetic energy (Equation \ref{RKE}) gives
\[\begin{align*} K_{rel} &\approx \left[\dfrac{1}{2}\left( \dfrac{u^2}{c^2}\right)\right] mc^2 \\[4pt] &\approx \dfrac{1}{2} mu^2 \\[4pt] &\approx K_{class}. \end{align*} \nonumber \]
That is, relativistic kinetic energy becomes the same as classical kinetic energy when \(u \ll c\).
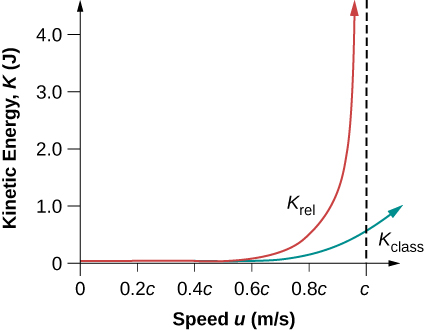
It is even more interesting to investigate what happens to kinetic energy when the speed of an object approaches the speed of light. We know that \(\gamma\) becomes infinite as \(u\) approaches \(c\), so that \(K_{rel}\) also becomes infinite as the velocity approaches the speed of light (Figure \(\PageIndex{2}\)). The increase in \(K_{rel}\) is far larger than in \(K_{class}\) as \(v\) approaches \(c\). An infinite amount of work (and, hence, an infinite amount of energy input) is required to accelerate a mass to the speed of light.
No object with mass can attain the speed of light.
The speed of light is the ultimate speed limit for any particle having mass. All of this is consistent with the fact that velocities less than c always add to less than \(c\). Both the relativistic form for kinetic energy and the ultimate speed limit being \(c\) have been confirmed in detail in numerous experiments. No matter how much energy is put into accelerating a mass, its velocity can only approach—not reach—the speed of light.
An electron has a velocity \(v = 0.990 c\).
- Calculate the kinetic energy in MeV of the electron.
- Compare this with the classical value for kinetic energy at this velocity. (The mass of an electron is \(9.11 \times 10^{-31}kg\).)
Strategy
The expression for relativistic kinetic energy is always correct, but for (a), it must be used because the velocity is highly relativistic (close to \(c\)). First, we calculate the relativistic factor \(\gamma\), and then use it to determine the relativistic kinetic energy. For (b), we calculate the classical kinetic energy (which would be close to the relativistic value if \(v\) were less than a few percent of \(c\)) and see that it is not the same.
Solution for (a)
- Identify the knowns: \(v = 0.990c\); \(m = 9.11 \times 10^{-31}kg\)
- Identify the unknown: \(K_{rel}\).
- Express the answer as an equation: \(K_{rel} = (\gamma - 1)mc^2\) with \(\gamma = \dfrac{1}{\sqrt{1 - u^2/c^2}}.\)
- Do the calculation. First calculate \(\gamma\). Keep extra digits because this is an intermediate calculation: \[\begin{align*} \gamma &= \dfrac{1}{\sqrt{1 - u^2/c^2}} \nonumber \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{(0.990c)^2}{c^2}}} \nonumber \\[4pt] &= 7.0888. \end{align*} \nonumber \] Now use this value to calculate the kinetic energy (Equatoin \ref{RKE}):
\[\begin{align*} K_{rel} &= (\gamma - 1)mc^2 \nonumber \\[4pt] &= (7.0888 - 1)(9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s^2) \nonumber \\[4pt] &= 4.9922 \times 10^{−13}\, J \end{align*} \nonumber \]
- Convert units:
\[\begin{align*} K_{rel} &= (4.9922 \times 10^{−13}\, J) \left(\dfrac{1\, MeV}{1.60 \times 10^{−13} J}\right) \\[4pt] &= 3.12\, MeV.\end{align*} \nonumber \]
Solution for (b)
- List the knowns: \(v = 0.990c\); \(m = 9.11 \times 10^{−31}kg\).
- List the unknown: \(K_{rel}\)
- Express the answer as an equation:
- Do the calculation:
\[\begin{align*} K_{class} &= \dfrac{1}{2} mu^2 \\[4pt] &= \dfrac{1}{2} (9.11 \times 10^{-31} kg)(0.990)^2(3.00 \times 10^8\, m/s)^2 \\[4pt] &= 4.0179 \times 10^{−14}J.\end{align*} \nonumber \]
- Convert units:
\[\begin{align*} K_{class} &= 4.0179 \times 10^{-14} J \left(\dfrac{1\, MeV}{1.60 \times 10^{-13} J}\right) \\[4pt] &= 0.251\, MeV.\end{align*} \nonumber \]
Significance
As might be expected, because the velocity is 99.0% of the speed of light, the classical kinetic energy differs significantly from the correct relativistic value. Note also that the classical value is much smaller than the relativistic value. In fact, \(K_{rel}/K_{class} = 12.4\) in this case. This illustrates how difficult it is to get a mass moving close to the speed of light. Much more energy is needed than predicted classically. Ever-increasing amounts of energy are needed to get the velocity of a mass a little closer to that of light. An energy of 3 MeV is a very small amount for an electron, and it can be achieved with present-day particle accelerators. SLAC, for example, can accelerate electrons to over \(50 \times 10^9 eV = 50,000\, MeV\).
Is there any point in getting v a little closer to c than 99.0% or 99.9%? The answer is yes. We learn a great deal by doing this. The energy that goes into a high-velocity mass can be converted into any other form, including into entirely new particles. In the Large Hadron Collider in Figure \(\PageIndex{1}\), charged particles are accelerated before entering the ring-like structure. There, two beams of particles are accelerated to their final speed of about 99.7% the speed of light in opposite directions, and made to collide, producing totally new species of particles. Most of what we know about the substructure of matter and the collection of exotic short-lived particles in nature has been learned this way. Patterns in the characteristics of these previously unknown particles hint at a basic substructure for all matter. These particles and some of their characteristics will be discussed in a later chapter on particle physics.
Total Relativistic Energy
The expression for kinetic energy can be rearranged to:
\[\begin{align*} E &= \dfrac{mc^2}{\sqrt{1 - u^2/c^2}} \\[4pt] &= K + mc^2. \end{align*} \nonumber \]
Einstein argued in a separate article, also later published in 1905, that if the energy of a particle changes by \(\Delta E\), its mass changes by \(\Delta m = \Delta E/C^2\). Abundant experimental evidence since then confirms that \(mc^2\) corresponds to the energy that the particle of mass \(m\) has when at rest. For example, when a neutral pion of mass \(m\) at rest decays into two photons, the photons have zero mass but are observed to have total energy corresponding to \(mc^2\) for the pion. Similarly, when a particle of mass \(m\) decays into two or more particles with smaller total mass, the observed kinetic energy imparted to the products of the decay corresponds to the decrease in mass. Thus, \(E\) is the total relativistic energy of the particle, and \(mc^2\) is its rest energy.
Total energy (\(E\)) of a particle is
\[E = \gamma mc^2 \nonumber \]
where \(m\) is mass, \(c\) is the speed of light, \(\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}}\), and \(u\) is the velocity of the mass relative to an observer.
Rest energy of an object is
\[E_0 = mc^2. \label{rest energy} \]
Equation \ref{rest energy} is the correct form of Einstein’s most famous equation, which for the first time showed that energy is related to the mass of an object at rest. For example, if energy is stored in the object, its rest mass increases. This also implies that mass can be destroyed to release energy. The implications of these first two equations regarding relativistic energy are so broad that they were not completely recognized for some years after Einstein published them in 1905, nor was the experimental proof that they are correct widely recognized at first. Einstein, it should be noted, did understand and describe the meanings and implications of his theory.
Calculate the rest energy of a 1.00-g mass.
Strategy
One gram is a small mass—less than one-half the mass of a penny. We can multiply this mass, in SI units, by the speed of light squared to find the equivalent rest energy.
Solution
- Identify the knowns: \(m = 1.00 \times 10^{-3} kg\); \(c = 3.00 \times 10^8 m/s\).
- Identify the unknown: \(E_0\).
- Express the answer as an equation: \(E_0 = mc^2\).
- Do the calculation:
\[E_0 = mc^2 = (1.00 \times 10^{-3} kg) (3.00 \times 10^8 m/s)^2 = 9.00 \times 10^{13} kg \cdot m^2/s^2. \nonumber \]
- Convert units. Noting that \(1\, kg \cdot m^2/s^2 = 1\, J\), we see the rest energy is:
\[E_0 = 9.00 \times 10^{13}\, J. \nonumber \]
Significance
This is an enormous amount of energy for a 1.00-g mass. Rest energy is large because the speed of light c is a large number and \(c^2\) is a very large number, so that \(mc^2\) is huge for any macroscopic mass. The \(9.00 \times 10^{13} J\) rest mass energy for 1.00 g is about twice the energy released by the Hiroshima atomic bomb and about 10,000 times the kinetic energy of a large aircraft carrier.
Today, the practical applications of the conversion of mass into another form of energy, such as in nuclear weapons and nuclear power plants, are well known. But examples also existed when Einstein first proposed the correct form of relativistic energy, and he did describe some of them. Nuclear radiation had been discovered in the previous decade, and it had been a mystery as to where its energy originated. The explanation was that, in some nuclear processes, a small amount of mass is destroyed and energy is released and carried by nuclear radiation. But the amount of mass destroyed is so small that it is difficult to detect that any is missing. Although Einstein proposed this as the source of energy in the radioactive salts then being studied, it was many years before there was broad recognition that mass could be and, in fact, commonly is, converted to energy (Figure \(\PageIndex{4}\)).

Because of the relationship of rest energy to mass, we now consider mass to be a form of energy rather than something separate. There had not been even a hint of this prior to Einstein’s work. Energy-mass equivalence is now known to be the source of the sun’s energy, the energy of nuclear decay, and even one of the sources of energy keeping Earth’s interior hot.
Stored Energy and Potential Energy
What happens to energy stored in an object at rest, such as the energy put into a battery by charging it, or the energy stored in a toy gun’s compressed spring? The energy input becomes part of the total energy of the object and thus increases its rest mass. All stored and potential energy becomes mass in a system. In seeming contradiction, the principle of conservation of mass (meaning total mass is constant) was one of the great laws verified by nineteenth-century science. Why was it not noticed to be incorrect? The following example helps answer this question.
A car battery is rated to be able to move 600 ampere-hours \((A \cdot h)\) of charge at 12.0 V.
- Calculate the increase in rest mass of such a battery when it is taken from being fully depleted to being fully charged, assuming none of the chemical reactants enter or leave the battery.
- What percent increase is this, given that the battery’s mass is 20.0 kg?
Strategy
In part (a), we first must find the energy stored as chemical energy \(E_{batt}\) in the battery, which equals the electrical energy the battery can provide. Because \(E_{batt} = qV\), we have to calculate the charge \(q\) in \(600\, A \cdot h\), which is the product of the current \(I\) and the time \(t\). We then multiply the result by 12.0 V. We can then calculate the battery’s increase in mass using \(E_{batt} = (\Delta m)c^2\). Part (b) is a simple ratio converted into a percentage.
Solution for (a)
- Identify the knowns: \[I \cdot t = 600\, A \cdot h;\, V = 12.0\, V;\, c = 3.00 \times 10^8\, m/s. \nonumber \]
- Identify the unknown: \(\Delta m\).
- Express the answer as an equation: \[\begin{align*} E_{batt} &= (\Delta m)c^2 \\[4pt] \Delta m &= \dfrac{E_{batt}}{c^2} \\[4pt] &= \dfrac{qV}{c^2} \\[4pt] &= \dfrac{(It)V}{c^2}.\end{align*} \nonumber \]
- Do the calculation: \[\Delta m = \dfrac{(600\, A \cdot h)(12.0\, V)}{(3.00 \times 10^8)^2}. \nonumber \]
- Write amperes A as coulombs per second (C/s), and convert hours into seconds:
\[\begin{align*}\Delta m &= \dfrac{(600\, C/s \cdot h)\left(\dfrac{3600\, s}{1\, h}\right)(12.0\, J/C)}{(3.00 \times 10^8\, m/s)^2} \\[4pt] &= 2.88 \times 10^{-10}\, kg. \end{align*} \nonumber \]
where we have used the conversion \(1\, kg \cdot m^2/s^2 = 1\, J.\).
Solution for (b)
For part (b):
- Identify the knowns: \(\delta m = 2.88 \times 10^{-10}kg\); \(m = 20.0\, kg\).
- Identify the unknown: % change.
- Express the answer as an equation: \[\%\, increase = \dfrac{\delta m}{m} \times 100\%. \nonumber \]
- Do the calculation:
\[\begin{align*} \%\, increase &= \dfrac{\Delta m}{m} \times 100\% \\[4pt] &= \dfrac{2.88 \times 10^{-10}\, kg}{20.0\, kg} \times 100\% \\[4pt] &= 1.44 \times 10^{-9} \% \end{align*} \nonumber \]
Significance
Both the actual increase in mass and the percent increase are very small, because energy is divided by \(c^2\), a very large number. We would have to be able to measure the mass of the battery to a precision of a billionth of a percent, or 1 part in \(10^{11}\), to notice this increase. It is no wonder that the mass variation is not readily observed. In fact, this change in mass is so small that we may question how anyone could verify that it is real. The answer is found in nuclear processes in which the percentage of mass destroyed is large enough to be measured accurately. The mass of the fuel of a nuclear reactor, for example, is measurably smaller when its energy has been used. In that case, stored energy has been released (converted mostly into thermal energy to power electric generators) and the rest mass has decreased. A decrease in mass also occurs from using the energy stored in a battery, except that the stored energy is much greater in nuclear processes, making the change in mass measurable in practice as well as in theory.
Relativistic Energy and Momentum
We know classically that kinetic energy and momentum are related to each other, because:
\[K_{class} = \dfrac{p^2}{2m} = \dfrac{(mu)^2}{2m} = \dfrac{1}{2}mu^2. \nonumber \]
Relativistically, we can obtain a relationship between energy and momentum by algebraically manipulating their defining equations. This yields:
\[E^2 = (pc)^2 + (mc^2)^2, \label{5.11} \]
where \(E\) is the relativistic total energy,
\[E = \dfrac{mc^2 }{\sqrt{1 - u^2/c^2}} \nonumber \]
and \(p\) is the relativistic momentum. This relationship between relativistic energy and relativistic momentum is more complicated than the classical version, but we can gain some interesting new insights by examining it. First, total energy is related to momentum and rest mass. At rest, momentum is zero, and the equation gives the total energy to be the rest energy \(mc^2\) (so this equation is consistent with the discussion of rest energy above). However, as the mass is accelerated, its momentum \(p\) increases, thus increasing the total energy. At sufficiently high velocities, the rest energy term \((mc^2)^2\) becomes negligible compared with the momentum term \((pc)^2\); thus, \(E = pc\) at extremely relativistic velocities.
If we consider momentum \(p\) to be distinct from mass, we can determine the implications of the equation
\[E^2 = (pc)^2 + (mc^2)^2, \nonumber \]
for a particle that has no mass. If we take \(m\) to be zero in this equation, then \(E = pc,\, orp = E/c\). Massless particles have this momentum. There are several massless particles found in nature, including photons (which are packets of electromagnetic radiation). Another implication is that a massless particle must travel at speed c and only at speed c. It is beyond the scope of this text to examine the relationship in the equation \(E^2 = (pc)^2 + (mc^2)^2\) in detail, but you can see that the relationship has important implications in special relativity.
What is the kinetic energy of an electron if its speed is \(0.992c\)?
- Answer
-
\[ \begin{align*} K_{rel} &= (\gamma - 1)mc^2 = \left(\dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} - 1 \right) mc^2 \nonumber \\[4pt] &= \left(\dfrac{1}{\sqrt{1 - \dfrac{(0.992 c)^2}{c^2}}} - 1 \right) (9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s)^2 \nonumber \\[4pt] &= 5.67 \times 10^{-13}\, J \end{align*} \nonumber \]


