12.A: Sources of Magnetic Fields (Answers)
- Page ID
- 10256
Check Your Understanding
12.1. 1.41 meters
12.2. \(\displaystyle \frac{μ_0I}{2R}\)
12.3. 4 amps flowing out of the page
12.4. Both have a force per unit length of \(\displaystyle 9.23×10^{−12}N/m\)
12.5. 0.608 meters
12.6. In these cases the integrals around the Ampèrian loop are very difficult because there is no symmetry, so this method would not be useful.
12.7. a. 1.00382;
b. 1.00015
12.8. a. \(\displaystyle 1.0×10^{−4}T\);
b. 0.60 T;
c. \(\displaystyle 6.0×10^3\)
Conceptual Questions
1. Biot-Savart law’s advantage is that it works with any magnetic field produced by a current loop. The disadvantage is that it can take a long time.
3. If you were to go to the start of a line segment and calculate the angle \(\displaystyle θ\) to be approximately \(\displaystyle 0°\), the wire can be considered infinite. This judgment is based also on the precision you need in the result.
5. You would make sure the currents flow perpendicular to one another.
7. A magnetic field line gives the direction of the magnetic field at any point in space. The density of magnetic field lines indicates the strength of the magnetic field.
9. The spring reduces in length since each coil with have a north pole-produced magnetic field next to a south pole of the next coil.
11. Ampère’s law is valid for all closed paths, but it is not useful for calculating fields when the magnetic field produced lacks symmetry that can be exploited by a suitable choice of path.
13. If there is no current inside the loop, there is no magnetic field (see Ampère’s law). Outside the pipe, there may be an enclosed current through the copper pipe, so the magnetic field may not be zero outside the pipe.
15. The bar magnet will then become two magnets, each with their own north and south poles. There are no magnetic monopoles or single pole magnets.
Problems
17. \(\displaystyle 5.66×10^{−5}T\)
19. \(\displaystyle B=\frac{μ_oI}{8}(\frac{1}{a}−\frac{1}{b})\) out of the page
21. \(\displaystyle a=\frac{2R}{π}\); the current in the wire to the right must flow up the page.
23. 20 A
25. Both answers have the magnitude of magnetic field of \(\displaystyle 4.5×10^{−5}T\).
27. At P1, the net magnetic field is zero. At P2, \(\displaystyle B=\frac{3μ_oI}{8πa}\) into the page.
29. The magnetic field is at a minimum at distance a from the top wire, or half-way between the wires.
31. a. \(\displaystyle F/l=8×10^{−6}\) N/m away from the other wire;
b. \(\displaystyle F/l=8×10^{−6}\) N/m toward the other wire
33. \(\displaystyle B=\frac{μ_oIa}{2πb^2}\) into the page
35. 0.019 m
37. \(\displaystyle 6.28×10^{−5}T\)
39. \(\displaystyle B=\frac{\mu_{o} I R^{2}}{\left(\left(\frac{d}{2}\right)^{2}+R^{2}\right)^{3 / 2}}\)
41. a. \(\displaystyle μ0I;\)
b. 0;
c. \(\displaystyle μ0I\);
d. 0
43. a. \(\displaystyle 3μ_0I\);
b. 0;
c. \(\displaystyle 7μ_0I\);
d. \(\displaystyle −2μ_0I\)
45. at the radius R
47.
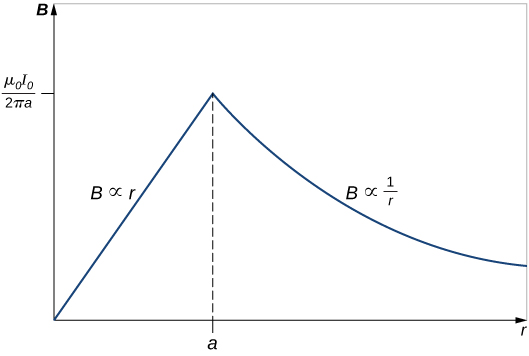
49. \(\displaystyle B=1.3×10^{−2}T\)
51. roughly eight turns per cm
53. \(\displaystyle B=\frac{1}{2}μ_0nI\)
55. 0.0181 A
57. 0.0008 T
59. 317.31
61. \(\displaystyle 2.1×10^{−4}A⋅m^2\) \(\displaystyle 2.7A\)
63. 0.18 T
Additional Problems
65. \(\displaystyle B=6.93×10^{−5}T\)
67. \(\displaystyle 3.2×10^{−19}N\) in an arc away from the wire
69. a. above and below \(\displaystyle B=μ_0j\), in the middle \(\displaystyle B=0\);
b. above and below \(\displaystyle B=0\), in the middle \(\displaystyle B=μ_0j\)
71. \(\displaystyle \frac{dB}{B}=−\frac{dr}{r}\)
73. a. 52778 turns;
b. 0.10 T
75. \(\displaystyle B_1(x)=\frac{μ_0IR^2}{2(R^2+z^2)^{3/2}}\)
77. \(\displaystyle B=\frac{μ_0σω}{2}R\)
79. derivation
81. derivation
83. As the radial distance goes to infinity, the magnetic fields of each of these formulae go to zero.
85. a. \(\displaystyle B=\frac{μ_0I}{2πr}\);
b. \(\displaystyle B=\frac{μ_0J_0r^2}{3R}\)
87. \(\displaystyle B(r)=μ_0NI/2πr\)
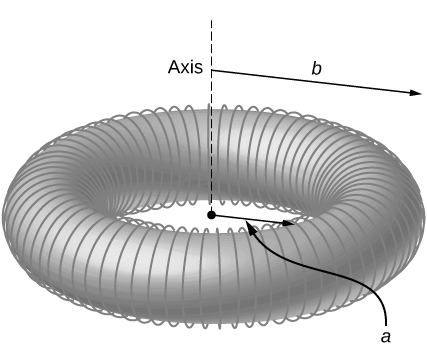
Challenge Problems
89. \(\displaystyle B=\frac{μ_0I}{2πx}\).
91. a. \(\displaystyle B=\frac{μ_0σω}{2}[\frac{2h^2+R^2}{\sqrt{R^2+h^0}}]\);
b. \(\displaystyle B=4.09×10^{−5}T\), 82% of Earth’s magnetic field
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


