15.2: AC Sources
- Page ID
- 4442
By the end of the section, you will be able to:
- Explain the differences between direct current (dc) and alternating current (ac)
- Define characteristic features of alternating current and voltage, such as the amplitude or peak and the frequency
Most examples dealt with so far in this book, particularly those using batteries, have constant-voltage sources. Thus, once the current is established, it is constant. Direct current (dc) is the flow of electric charge in only one direction. It is the steady state of a constant-voltage circuit.
Most well-known applications, however, use a time-varying voltage source. Alternating current (ac) is the flow of electric charge that periodically reverses direction. An ac is produced by an alternating emf, which is generated in a power plant, as described in Induced Electric Fields. If the ac source varies periodically, particularly sinusoidally, the circuit is known as an ac circuit. Examples include the commercial and residential power that serves so many of our needs.
The ac voltages and frequencies commonly used in businesses and homes vary around the world. In a typical house, the potential difference between the two sides of an electrical outlet alternates sinusoidally with a frequency of 60 or 50 Hz and an amplitude of 170 or 311 V, depending on whether you live in the United States or Europe, respectively. Most people know the potential difference for electrical outlets is 120 V or 220 V in the US or Europe, but as explained later in the chapter, these voltages are not the peak values given here but rather are related to the common voltages we see in our electrical outlets. Figure \(\PageIndex{1}\) shows graphs of voltage and current versus time for typical dc and ac power in the United States.
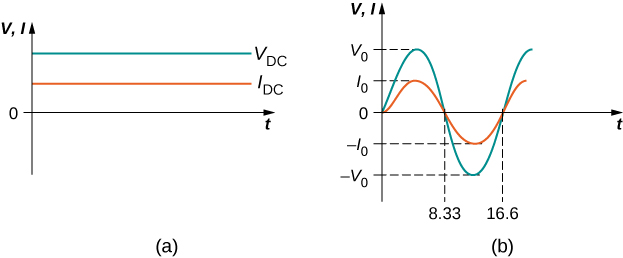
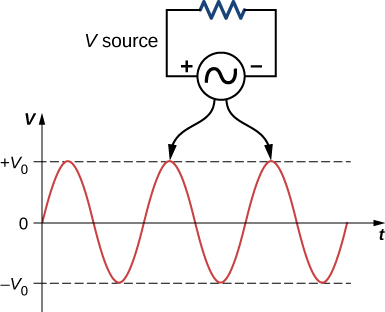
Suppose we hook up a resistor to an ac voltage source and determine how the voltage and current vary in time across the resistor. Figure \(\PageIndex{2}\) shows a schematic of a simple circuit with an ac voltage source. The voltage fluctuates sinusoidally with time at a fixed frequency, as shown, on either the battery terminals or the resistor. Therefore, the ac voltage, or the “voltage at a plug,” can be given by
\[v(t) = V_0 \, \sin \, \omega t,\]
where
- \(v\) is the voltage at time \(t\),
- \(V_0\) is the peak voltage, and
- \(\omega\) is the angular frequency in radians per second.
For a typical house in the United States, \(V_0 = 156 \, V\) and \(\omega = 120 \pi \, rad/s\), whereas in Europe, \(V_0 = 311 \, V\) and \(\omega = 100 \pi \, rad/s\).
For this simple resistance circuit, \(I = V/R\), so the ac current, meaning the current that fluctuates sinusoidally with time at a fixed frequency, is
\[i(t) = I_0 \, \sin \, \omega t,\]
where
- \(i(t)\) is the current at time \(t\) and
- \(I_0\) is the peak current and is equal to \(V_0/R\).
For this example, the voltage and current are said to be in phase, meaning that their sinusoidal functional forms have peaks, troughs, and nodes in the same place. They oscillate in sync with each other, as shown in Figure \(\PageIndex{1b}\). In these equations, and throughout this chapter, we use lowercase letters (such as \(i\)) to indicate instantaneous values and capital letters (such as \(I\)) to indicate maximum, or peak, values.
Current in the resistor alternates back and forth just like the driving voltage, since \(I = V/R\). If the resistor is a fluorescent light bulb, for example, it brightens and dims 120 times per second as the current repeatedly goes through zero. A 120-Hz flicker is too rapid for your eyes to detect, but if you wave your hand back and forth between your face and a fluorescent light, you will see the stroboscopic effect of ac.
If a European ac voltage source is considered, what is the time difference between the zero crossings on an ac voltage-versus-time graph?
Solution
10 ms
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


