13.E: Gravitation (Exercises)
- Page ID
- 6549
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Conceptual Questions
13.1 Newton's Law of Universal Gravitation
- Action at a distance, such as is the case for gravity, was once thought to be illogical and therefore untrue. What is the ultimate determinant of the truth in science, and why was this action at a distance ultimately accepted?
- In the law of universal gravitation, Newton assumed that the force was proportional to the product of the two masses (~m1m2). While all scientific conjectures must be experimentally verified, can you provide arguments as to why this must be? (You may wish to consider simple examples in which any other form would lead to contradictory results.)
13.2 Gravitation Near Earth's Surface
- Must engineers take Earth’s rotation into account when constructing very tall buildings at any location other than the equator or very near the poles?
13.3 Gravitational Potential Energy and Total Energy
- It was stated that a satellite with negative total energy is in a bound orbit, whereas one with zero or positive total energy is in an unbounded orbit. Why is this true? What choice for gravitational potential energy was made such that this is true?
- It was shown that the energy required to lift a satellite into a low Earth orbit (the change in potential energy) is only a small fraction of the kinetic energy needed to keep it in orbit. Is this true for larger orbits? Is there a trend to the ratio of kinetic energy to change in potential energy as the size of the orbit increases?
13.4 Satellite Orbits and Energy
- One student argues that a satellite in orbit is in free fall because the satellite keeps falling toward Earth. Another says a satellite in orbit is not in free fall because the acceleration due to gravity is not 9.80 m/s2. With whom do you agree with and why?
- Many satellites are placed in geosynchronous orbits. What is special about these orbits? For a global communication network, how many of these satellites would be needed?
13.5 Kepler's Laws of Planetary Motion
- Are Kepler’s laws purely descriptive, or do they contain causal information?
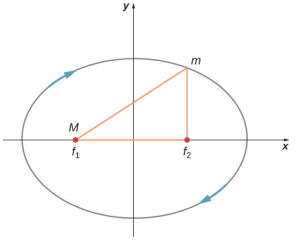
- In the diagram below for a satellite in an elliptical orbit about a much larger mass, indicate where its speed is the greatest and where it is the least. What conservation law dictates this behavior? Indicate the directions of the force, acceleration, and velocity at these points. Draw vectors for these same three quantities at the two points where the yaxis intersects (along the semi-minor axis) and from this determine whether the speed is increasing decreasing, or at a max/min.
13.6 Tidal Forces
- As an object falls into a black hole, tidal forces increase. Will these tidal forces always tear the object apart as it approaches the Schwarzschild radius? How does the mass of the black hole and size of the object affect your answer?
13.7 Einstein's Theory of Gravity
- The principle of equivalence states that all experiments done in a lab in a uniform gravitational field cannot be distinguished from those done in a lab that is not in a gravitational field but is uniformly accelerating. For the latter case, consider what happens to a laser beam at some height shot perfectly horizontally to the floor, across the accelerating lab. (View this from a nonaccelerating frame outside the lab.) Relative to the height of the laser, where will the laser beam hit the far wall? What does this say about the effect of a gravitational field on light? Does the fact that light has no mass make any difference to the argument?
- As a person approaches the Schwarzschild radius of a black hole, outside observers see all the processes of that person (their clocks, their heart rate, etc.) slowing down, and coming to a halt as they reach the Schwarzschild radius. (The person falling into the black hole sees their own processes unaffected.) But the speed of light is the same everywhere for all observers. What does this say about space as you approach the black hole?
Problems
13.1 Newton's Law of Universal Gravitation
- Evaluate the magnitude of gravitational force between two 5-kg spherical steel balls separated by a center-to-center distance of 15 cm.
- Estimate the gravitational force between two sumo wrestlers, with masses 220 kg and 240 kg, when they are embraced and their centers are 1.2 m apart.
- Astrology makes much of the position of the planets at the moment of one’s birth. The only known force a planet exerts on Earth is gravitational. (a) Calculate the gravitational force exerted on a 4.20-kg baby by a 100-kg father 0.200 m away at birth (he is assisting, so he is close to the child). (b) Calculate the force on the baby due to Jupiter if it is at its closest distance to Earth, some 6.29 x 1011 m away. How does the force of Jupiter on the baby compare to the force of the father on the baby? Other objects in the room and the hospital building also exert similar gravitational forces. (Of course, there could be an unknown force acting, but scientists first need to be convinced that there is even an effect, much less that an unknown force causes it.)
- A mountain 10.0 km from a person exerts a gravitational force on him equal to 2.00% of his weight. (a) Calculate the mass of the mountain. (b) Compare the mountain’s mass with that of Earth. (c) What is unreasonable about these results? (d) Which premises are unreasonable or inconsistent? (Note that accurate gravitational measurements can easily detect the effect of nearby mountains and variations in local geology.)
- The International Space Station has a mass of approximately 370,000 kg. (a) What is the force on a 150-kg suited astronaut if she is 20 m from the center of mass of the station? (b) How accurate do you think your answer would be?

- Asteroid Toutatis passed near Earth in 2006 at four times the distance to our Moon. This was the closest approach we will have until 2060. If it has mass of 5.0 x 1013 kg , what force did it exert on Earth at its closest approach?
- (a) What was the acceleration of Earth caused by asteroid Toutatis (see previous problem) at its closest approach? (b) What was the acceleration of Toutatis at this point?
13.2 Gravitation Near Earth's Surface
- (a) Calculate Earth’s mass given the acceleration due to gravity at the North Pole is measured to be 9.832 m/s2 and the radius of the Earth at the pole is 6356 km. (b) Compare this with the NASA’s Earth Fact Sheet value of 5.9726 x 1024 kg.
- (a) What is the acceleration due to gravity on the surface of the Moon? (b) On the surface of Mars? The mass of Mars is 6.418 x 1023 kg and its radius is 3.38 x 106 m.
- (a) Calculate the acceleration due to gravity on the surface of the Sun. (b) By what factor would your weight increase if you could stand on the Sun? (Never mind that you cannot.)
- The mass of a particle is 15 kg. (a) What is its weight on Earth? (b) What is its weight on the Moon? (c) What is its mass on the Moon? (d) What is its weight in outer space far from any celestial body? (e) What is its mass at this point?
- On a planet whose radius is 1.2 x 107 m, the acceleration due to gravity is 18 m/s2. What is the mass of the planet?
- The mean diameter of the planet Saturn is 1.2 x 108 m, and its mean mass density is 0.69 g/cm3. Find the acceleration due to gravity at Saturn’s surface.
- The mean diameter of the planet Mercury is 4.88 x 106 m, and the acceleration due to gravity at its surface is 3.78 m/s2. Estimate the mass of this planet.
- The acceleration due to gravity on the surface of a planet is three times as large as it is on the surface of Earth. The mass density of the planet is known to be twice that of Earth. What is the radius of this planet in terms of Earth’s radius?
- A body on the surface of a planet with the same radius as Earth’s weighs 10 times more than it does on Earth. What is the mass of this planet in terms of Earth’s mass?
13.3 Gravitational Potential Energy and Total Energy
- Find the escape speed of a projectile from the surface of Mars.
- Find the escape speed of a projectile from the surface of Jupiter.
- What is the escape speed of a satellite located at the Moon’s orbit about Earth? Assume the Moon is not nearby.
- (a) Evaluate the gravitational potential energy between two 5.00-kg spherical steel balls separated by a center-to-center distance of 15.0 cm. (b) Assuming that they are both initially at rest relative to each other in deep space, use conservation of energy to find how fast will they be traveling upon impact. Each sphere has a radius of 5.10 cm.
- An average-sized asteroid located 5.0 x 107 km from Earth with mass 2.0 x 1013 kg is detected headed directly toward Earth with speed of 2.0 km/s. What will its speed be just before it hits our atmosphere? (You may ignore the size of the asteroid.)
- (a) What will be the kinetic energy of the asteroid in the previous problem just before it hits Earth? b) Compare this energy to the output of the largest fission bomb, 2100 TJ. What impact would this have on Earth?
- (a) What is the change in energy of a 1000-kg payload taken from rest at the surface of Earth and placed at rest on the surface of the Moon? (b) What would be the answer if the payload were taken from the Moon’s surface to Earth? Is this a reasonable calculation of the energy needed to move a payload back and forth?
13.4 Satellite Orbits and Energy
- If a planet with 1.5 times the mass of Earth was traveling in Earth’s orbit, what would its period be?
- Two planets in circular orbits around a star have speeds of v and 2v. (a) What is the ratio of the orbital radii of the planets? (b) What is the ratio of their periods?
- Using the average distance of Earth from the Sun, and the orbital period of Earth, (a) find the centripetal acceleration of Earth in its motion about the Sun. (b) Compare this value to that of the centripetal acceleration at the equator due to Earth’s rotation.
- What is the orbital radius of an Earth satellite having a period of 1.00 h? (b) What is unreasonable about this result?
- Calculate the mass of the Sun based on data for Earth’s orbit and compare the value obtained with the Sun’s actual mass.
- Find the mass of Jupiter based on the fact that Io, its innermost moon, has an average orbital radius of 421,700 km and a period of 1.77 days.
- Astronomical observations of our Milky Way galaxy indicate that it has a mass of about 8.0 x 1011 solar masses. A star orbiting on the galaxy’s periphery is about 6.0 x 104 light-years from its center. (a) What should the orbital period of that star be? (b) If its period is 6.0 x 107 years instead, what is the mass of the galaxy? Such calculations are used to imply the existence of other matter, such as a very massive black hole at the center of the Milky Way.
- (a) In order to keep a small satellite from drifting into a nearby asteroid, it is placed in orbit with a period of 3.02 hours and radius of 2.0 km. What is the mass of the asteroid? (b) Does this mass seem reasonable for the size of the orbit?
- The Moon and Earth rotate about their common center of mass, which is located about 4700 km from the center of Earth. (This is 1690 km below the surface.) (a) Calculate the acceleration due to the Moon’s gravity at that point. (b) Calculate the centripetal acceleration of the center of Earth as it rotates about that point once each lunar month (about 27.3 d) and compare it with the acceleration found in part (a). Comment on whether or not they are equal and why they should or should not be.
- The Sun orbits the Milky Way galaxy once each 2.60 x 108 years, with a roughly circular orbit averaging a radius of 3.00 x 104 light-years. (A light-year is the distance traveled by light in 1 year.) Calculate the centripetal acceleration of the Sun in its galactic orbit. Does your result support the contention that a nearly inertial frame of reference can be located at the Sun? (b) Calculate the average speed of the Sun in its galactic orbit. Does the answer surprise you?
- A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for Earth in Appendix D.
13.5 Kepler's Laws of Planetary Motion
- Calculate the mass of the Sun based on data for average Earth’s orbit and compare the value obtained with the Sun’s commonly listed value of 1.989 x 1030 kg.
- Io orbits Jupiter with an average radius of 421,700 km and a period of 1.769 days. Based upon these data, what is the mass of Jupiter?
- The “mean” orbital radius listed for astronomical objects orbiting the Sun is typically not an integrated average but is calculated such that it gives the correct period when applied to the equation for circular orbits. Given that, what is the mean orbital radius in terms of aphelion and perihelion?
- The perihelion of Halley’s comet is 0.586 AU and the aphelion is 17.8 AU. Given that its speed at perihelion is 55 km/s, what is the speed at aphelion (1 AU = 1.496 x 1011 m)? (Hint: You may use either conservation of energy or angular momentum, but the latter is much easier.)
- The perihelion of the comet Lagerkvist is 2.61 AU and it has a period of 7.36 years. Show that the aphelion for this comet is 4.95 AU.
- What is the ratio of the speed at perihelion to that at aphelion for the comet Lagerkvist in the previous problem?
- Eros has an elliptical orbit about the Sun, with a perihelion distance of 1.13 AU and aphelion distance of 1.78 AU. What is the period of its orbit?
13.6 Tidal Forces
- (a) What is the difference between the forces on a 1.0-kg mass on the near side of Io and far side due to Jupiter? Io has a mean radius of 1821 km and a mean orbital radius about Jupiter of 421,700 km. (b) Compare this difference to that calculated for the difference for Earth due to the Moon calculated in Example 13.14. Tidal forces are the cause of Io’s volcanic activity.
- If the Sun were to collapse into a black hole, the point of no return for an investigator would be approximately 3 km from the center singularity. Would the investigator be able to survive visiting even 300 km from the center? Answer this by finding the difference in the gravitational attraction the black holes exerts on a 1.0-kg mass at the head and at the feet of the investigator.
- Consider Figure 13.23 in Tidal Forces. This diagram represents the tidal forces for spring tides. Sketch a similar diagram for neap tides. (Hint: For simplicity, imagine that the Sun and the Moon contribute equally. Your diagram would be the vector sum of two force fields (as in Figure 13.23), reduced by a factor of two, and superimposed at right angles.)
13.7 Einstein's Theory of Gravity
- What is the Schwarzschild radius for the black hole at the center of our galaxy if it has the mass of 4 million solar masses?
- What would be the Schwarzschild radius, in light years, if our Milky Way galaxy of 100 billion stars collapsed into a black hole? Compare this to our distance from the center, about 13,000 light years.
Additional Problems
- A neutron star is a cold, collapsed star with nuclear density. A particular neutron star has a mass twice that of our Sun with a radius of 12.0 km. (a) What would be the weight of a 100-kg astronaut on standing on its surface? (b) What does this tell us about landing on a neutron star?
- (a) How far from the center of Earth would the net gravitational force of Earth and the Moon on an object be zero? (b) Setting the magnitudes of the forces equal should result in two answers from the quadratic. Do you understand why there are two positions, but only one where the net force is zero?
- How far from the center of the Sun would the net gravitational force of Earth and the Sun on a spaceship be zero?
- Calculate the values of g at Earth’s surface for the following changes in Earth’s properties: (a) its mass is doubled and its radius is halved; (b) its mass density is doubled and its radius is unchanged; (c) its mass density is halved and its mass is unchanged.
- Suppose you can communicate with the inhabitants of a planet in another solar system. They tell you that on their planet, whose diameter and mass are 5.0 x 103 km and 3.6 x 1023 kg, respectively, the record for the high jump is 2.0 m. Given that this record is close to 2.4 m on Earth, what would you conclude about your extraterrestrial friends’ jumping ability?
- (a) Suppose that your measured weight at the equator is one-half your measured weight at the pole on a planet whose mass and diameter are equal to those of Earth. What is the rotational period of the planet? (b) Would you need to take the shape of this planet into account?
- A body of mass 100 kg is weighed at the North Pole and at the equator with a spring scale. What is the scale reading at these two points? Assume that g = 9.83 m/s2 at the pole.
- Find the speed needed to escape from the solar system starting from the surface of Earth. Assume there are no other bodies involved and do not account for the fact that Earth is moving in its orbit. [Hint: Equation 13.6 does not apply. Use Equation 13.5 and include the potential energy of both Earth and the Sun.
- Consider the previous problem and include the fact that Earth has an orbital speed about the Sun of 29.8 km/ s. (a) What speed relative to Earth would be needed and in what direction should you leave Earth? (b) What will be the shape of the trajectory?
- A comet is observed 1.50 AU from the Sun with a speed of 24.3 km/s. Is this comet in a bound or unbound orbit?
- An asteroid has speed 15.5 km/s when it is located 2.00 AU from the sun. At its closest approach, it is 0.400 AU from the Sun. What is its speed at that point?
- Space debris left from old satellites and their launchers is becoming a hazard to other satellites. (a) Calculate the speed of a satellite in an orbit 900 km above Earth’s surface. (b) Suppose a loose rivet is in an orbit of the same radius that intersects the satellite’s orbit at an angle of 90°. What is the velocity of the rivet relative to the satellite just before striking it? (c) If its mass is 0.500 g, and it comes to rest inside the satellite, how much energy in joules is generated by the collision? (Assume the satellite’s velocity does not change appreciably, because its mass is much greater than the rivet’s.)
- A satellite of mass 1000 kg is in circular orbit about Earth. The radius of the orbit of the satellite is equal to two times the radius of Earth. (a) How far away is the satellite? (b) Find the kinetic, potential, and total energies of the satellite.
- After Ceres was promoted to a dwarf planet, we now recognize the largest known asteroid to be Vesta, with a mass of 2.67 x 1020 kg and a diameter ranging from 578 km to 458 km. Assuming that Vesta is spherical with radius 520 km, find the approximate escape velocity from its surface.
- (a) Using the data in the previous problem for the asteroid Vesta, what would be the orbital period for a space probe in a circular orbit of 10.0 km from its surface? (b) Why is this calculation marginally useful at best?
- What is the orbital velocity of our solar system about the center of the Milky Way? Assume that the mass within a sphere of radius equal to our distance away from the center is about a 100 billion solar masses. Our distance from the center is 27,000 light years.
- (a) Using the information in the previous problem, what velocity do you need to escape the Milky Way galaxy from our present position? (b) Would you need to accelerate a spaceship to this speed relative to Earth?
- Circular orbits in Equation 13.10 for conic sections must have eccentricity zero. From this, and using Newton’s second law applied to centripetal acceleration, show that the value of α in Equation 13.10 is given by \(\alpha = \frac{L^{2}}{GMm^{2}}\) where L is the angular momentum of the orbiting body. The value of α is constant and given by this expression regardless of the type of orbit.
- Show that for eccentricity equal to one in Equation 13.10 for conic sections, the path is a parabola. Do this by substituting Cartesian coordinates, x and y, for the polar coordinates, r and \(\theta\), and showing that it has the general form for a parabola, x = ay2 + by + c.
- Using the technique shown in Satellite Orbits and Energy, show that two masses m1 and m2 in circular orbits about their common center of mass, will have total energy \(E = K + E = K_{1} + k_{2} - \frac{Gm_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{2r}\). We have shown the kinetic energy of both masses explicitly. (Hint: The masses orbit at radii r1 and r2, respectively, where r = r1 + r2. Be sure not to confuse the radius needed for centripetal acceleration with that for the gravitational force.)
- Given the perihelion distance, p, and aphelion distance, q, for an elliptical orbit, show that the velocity at perihelion, vp, is given by \(v_{p} = \sqrt{\frac{2GM_{Sun}}{(q + p)} \frac{q}{p}}\). (Hint: Use conservation of angular momentum to relate vp and vq, and then substitute into the conservation of energy equation.)
- Comet P/1999 R1 has a perihelion of 0.0570 AU and aphelion of 4.99 AU. Using the results of the previous problem, find its speed at aphelion. (Hint: The expression is for the perihelion. Use symmetry to rewrite the expression for aphelion.)
Challenge Problems
- A tunnel is dug through the center of a perfectly spherical and airless planet of radius R. Using the expression for g derived in Gravitation Near Earth’s Surface for a uniform density, show that a particle of mass m dropped in the tunnel will execute simple harmonic motion. Deduce the period of oscillation of m and show that it has the same period as an orbit at the surface.
- Following the technique used in Gravitation Near Earth’s Surface, find the value of g as a function of the radius r from the center of a spherical shell planet of constant density \(\rho\) with inner and outer radii Rin and Rout. Find g for both Rin < r < Rout and for r < Rin. Assuming the inside of the shell is kept airless, describe travel inside the spherical shell planet.
- Show that the areal velocity for a circular orbit of radius r about a mass M is \(\frac{\Delta A}{\Delta t} = \frac{1}{2} \sqrt{GMr}\). Does your expression give the correct value for Earth’s areal velocity about the Sun?
- Show that the period of orbit for two masses, m1 and m2, in circular orbits of radii r1 and r2, respectively, about their common center-of-mass, is given by \(T = 2 \pi \sqrt{\frac{r^{3}}{G(m_{1} + m_{2})}}\) where r = r1 + r2. (Hint: The masses orbit at radii r1 and r2, respectively where r = r1 + r2. Use the expression for the center-of-mass to relate the two radii and note that the two masses must have equal but opposite momenta. Start with the relationship of the period to the circumference and speed of orbit for one of the masses. Use the result of the previous problem using momenta in the expressions for the kinetic energy.)
- Show that for small changes in height h, such that h << RE, Equation 13.4 reduces to the expression \(\Delta\)U = mgh.
- Using Figure 13.9, carefully sketch a free body diagram for the case of a simple pendulum hanging at latitude lambda, labeling all forces acting on the point mass, m. Set up the equations of motion for equilibrium, setting one coordinate in the direction of the centripetal acceleration (toward P in the diagram), the other perpendicular to that. Show that the deflection angle \(\epsilon\), defined as the angle between the pendulum string and the radial direction toward the center of Earth, is given by the expression below. What is the deflection angle at latitude 45 degrees? Assume that Earth is a perfect sphere. \(\tan(\lambda + \epsilon) = \frac{g}{(g − \omega^{2} R_{E})} \tan \lambda\), where \(\omega\) is the angular velocity of Earth.
- (a) Show that tidal force on a small object of mass m, defined as the difference in the gravitational force that would be exerted on m at a distance at the near and the far side of the object, due to the gravitation at a distance R from M, is given by Ftidal = \(\frac{2GMm}{R^{3}} \Delta\)r where \(\Delta\)r is the distance between the near and far side and \(\Delta\)r << R . (b) Assume you are falling feet first into the black hole at the center of our galaxy. It has mass of 4 million solar masses. What would be the difference between the force at your head and your feet at the Schwarzschild radius (event horizon)? Assume your feet and head each have mass 5.0 kg and are 2.0 m apart. Would you survive passing through the event horizon?
- Find the Hohmann transfer velocities, \(\Delta\)vEllipseEarth and \(\Delta\)vEllipseMars, needed for a trip to Mars. Use Equation 13.7 to find the circular orbital velocities for Earth and Mars. Using Equation 13.4 and the total energy of the ellipse (with semi-major axis a), given by E = − \(\frac{GmM_{s}}{2a}\), find the velocities at Earth (perihelion) and at Mars (aphelion) required to be on the transfer ellipse. The difference, \(\Delta\)v, at each point is the velocity boost or transfer velocity needed.
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


