18.4: Motion in Two and Three Dimensions
- Page ID
- 7943
Check Your Understanding
4.1. (a) Taking the derivative with respect to time of the position function, we have \(\vec{v}\)(t) = 9.0t2 \(\hat{i}\) and \(\vec{v}\)(3.0s) = 81.0 \(\hat{i}\) m/s. (b) Since the velocity function is nonlinear, we suspect the average velocity is not equal to the instantaneous velocity. We check this and find$$\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} = \frac{\vec{r} (4.0\; s) - \vec{r} (2.0\; s)}{4.0\; s - 2.0\; s} = \frac{(188.0\; \hat{i} - 20.0\; \hat{i})\; m}{2.0\; s} = 84.0\; \hat{i}\; m/s,$$ which is different from \(\vec{v}\)(3.0 s) = 81.0 \(\hat{i}\) m/s.
4.2. The acceleration vector is constant and doesn’t change with time. If a, b, and c are not zero, then the velocity function must be linear in time. We have \(\vec{v}\)(t) = \(\int \vec{a}\)dt = \(\int\) (a \(\hat{i}\) + b \(\hat{j}\) + c \(\hat{k}\))dt = (a \(\hat{i}\) + b \(\hat{j}\) + c \(\hat{k}\))t m/s, since taking the derivative of the velocity function produces \(\vec{a}\)(t). If any of the components of the acceleration are zero, then that component of the velocity would be a constant.
4.3. (a) Choose the top of the cliff where the rock is thrown from the origin of the coordinate system. Although it is arbitrary, we typically choose time t = 0 to correspond to the origin. (b) The equation that describes the horizontal motion is x = x0 + vxt. With x0 = 0, this equation becomes x = vxt. (c) Equation 4.27 through Equation 4.29 and Equation 4.46 describe the vertical motion, but since y0 = 0 and v0y = 0, these equations simplify greatly to become y = \(\frac{1}{2}\)(v0y + vy)t = \(\frac{1}{2}\)vyt, vy = −gt, y = − \(\frac{1}{2}\)gt2, and vy2 = −2gy. (d) We use the kinematic equations to find the x and y components of the velocity at the point of impact. Using vy2 = −2gy and noting the point of impact is −100.0 m, we find the y component of the velocity at impact is vy = 44.3 m/s. We are given the x component, vx = 15.0 m/s, so we can calculate the total velocity at impact: v = 46.8 m/s and \(\theta\) = 71.3° below the horizontal.
4.4. The golf shot at 30°.
4.5. 134.0 cm/s
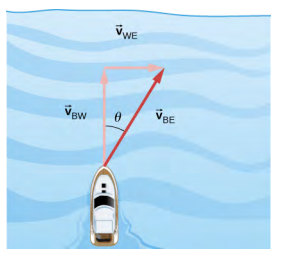
4.6. Labeling subscripts for the vector equation, we have B = boat, R = river, and E = Earth. The vector equation becomes \(\vec{v}_{BE}\) = \(\vec{v}_{BR}\) + \(\vec{v}_{RE}\). We have right triangle geometry shown in the figure below. Solving for \(\vec{v}_{BE}\), we have$$v_{BE} = \sqrt{v_{BR}^{2} + v_{RE}^{2}} = \sqrt{4.5^{2} + 3.0^{2}}$$$$v_{BE} = 5.4\; m/s, \quad \theta = \tan^{-1} \left(\dfrac{3.0}{4.5}\right) = 33.7^{o} \ldotp\]
Conceptual Questions
1. Straight line
3. The slope must be zero because the velocity vector is tangent to the graph of the position function.
5. No, motions in perpendicular directions are independent.
7. a. No; b. minimum at apex of trajectory and maximum at launch and impact; c. no, velocity is a vector; d. yes, where it lands
9. They both hit the ground at the same time.
11. Yes
13. If he is going to pass the ball to another player, he needs to keep his eyes on the reference frame in which the other players on the team are located.
15.
Problems
17. \(\vec{r}\) = 1.0 \(\hat{i}\) − 4.0 \(\hat{j}\) + 6.0 \(\hat{k}\)
19. \(\Delta \vec{r}_{Total}\) = 472.0 m \(\hat{i}\) + 80.3 m \(\hat{j}\)
21. Sum of displacements = −6.4 km \(\hat{i}\) + 9.4 km \(\hat{j}\)
23. a. \(\vec{v}\)(t) = 8.0t \(\hat{i}\) + 6.0t2 \(\hat{k}\), \(\vec{v}\)(0) = 0, \(\vec{v}\)(1.0) = 8.0 \(\hat{i}\) + 6.0 \(\hat{k}\) m/s
b. \(\vec{v}_{avg}\) = 4.0 \(\hat{i}\) + 2.0 \(\hat{k}\) m/s
25. \(\Delta \vec{r}_{1}\) = 20.00 m \(\hat{j}\), \(\Delta \vec{r}_{2}\) = (2.000 x 104 m) (cos 30° \(\hat{i}\) + sin 30° \(\hat{j}\)), \(\Delta \vec{r}\) = 1.700 x 104 m \(\hat{i}\) + 1.002 x 104 m \(\hat{j}\)
27. a. \(\vec{v}\)(t) = (4.0t \(\hat{i}\) + 3.0t \(\hat{j}\))m/s, \(\vec{r}\)(t) = (2.0t2 \(\hat{i}\) + \(\frac{3}{2}\)t2 \(\hat{j}\)) m
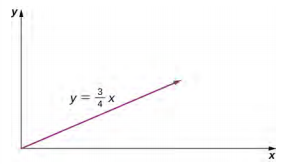
b. x(t) = 2.0t 2m, y(t) = \(\frac{3}{2}\)t2 m, t2 = \(\frac{x}{2} \Rightarrow\) y = \(\frac{3}{4}\)x
29. a. \(\vec{v}\)(t) = (6.0t \(\hat{i}\) − 21.0t2 \(\hat{j}\) + 10.0t−3 \(\hat{k}\)) m/s
b. \(\vec{a}\)(t) = (6.0 \(\hat{i}\) − 42.0t \(\hat{j}\) − 30t−4 \(\hat{k}\)) m/s2
c. \(\vec{v}\)(2.0s) = (12.0 \(\hat{i}\) − 84.0 \(\hat{j}\) + 1.25 \(\hat{k}\)) m/s
d. \(\vec{v}\)(1.0 s) = (6.0 \(\hat{i}\) − 21.0 \(\hat{j}\) + 10.0 \(\hat{k}\)) m/s, |\(\vec{v}\)(1.0 s)| = 24.0 m/s; \(\vec{v}\)(3.0 s) = (18.0 \(\hat{i}\) − 189.0 \(\hat{j}\) + 0.37 \(\hat{k}\)) m/s, |\(\vec{v}\)(3.0 s)| = 190.0 m/s
e. \(\vec{r}\)(t) = (3.0t2 \(\hat{i}\) − 7.0t3 \(\hat{j}\) − 5.0t−2 \(\hat{k}\)) cm, \(\vec{v}_{avg}\) = (9.0 \(\hat{i}\) − 49.0 \(\hat{j}\) − 6.3 \(\hat{k}\)) m/s
31. a. \(\vec{v}\)(t) = −sin(1.0t) \(\hat{i}\) + cos(1.0t) \(\hat{j}\) + \(\hat{k}\)
b. \(\vec{a}\)(t) = −cos(1.0t) \(\hat{i}\) − sin(1.0t) \(\hat{j}\)
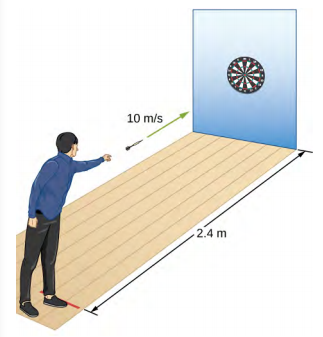
33. a. t = 0.55 s
b. x = 110 m
35. a. t = 0.24s, d = 0.28 m
b. They aim high.
37. a. t = 12.8 s, x = 5619 m
b. vy = 125.0 m/s, vx = 439.0 m/s, |\(\vec{v}\)| = 456.0 m/s
39. a. vy = v0y − gt, t = 10s, vy = 0, v0y = 98.0 m/s, v0 = 196.0 m/s
b. h = 490.0 m
c. v0x = 169.7 m/s, x = 3394.0 m
d. x = 2545.5 m, y = 367.5 m, \(\vec{s}\) = 2545.5 m \(\hat{i}\) + 367.5 m \(\hat{j}\)
41. −100 m = (−2.0 m/s)t − (4.9 m/s2)t2, t = 4.3 s, x = 86.0 m
43. RMoon = 48 m
45. a. v0y= 24 m/s, vy2 = v0y2 − 2gy \(\Rightarrow\) h = 23.4 m
b. t = 3 s, v0x = 18 m/s, x = 54 m
c. y = −100 m, y0 = 0, y − y0 = v0y, t − \(\frac{1}{2}\)gt2 − 100 = 24t − 4.9t2 \(\Rightarrow\) t = 7.58 s
d. x = 136.44 m
e.$$\begin{split} t & = 2.0\; s, y = 28.4\; m, x = 36\; m \\ t & = 4.0\; s, y = 17.6\; m, x = 22.4\; m \\ t & = 6.0\; s, y = −32.4\; m, x = 108\; m \end{split}\]
47. v0y= 12.9 m/s, y − y0 = v0yt − \(\frac{1}{2}\)gt2 − 20.0 = 12.9t − 4.9t2
t = 3.7 s, v0x = 15.3 m/s \(\Rightarrow\) x = 56.7 m
So the golfer’s shot lands 13.3 m short of the green.
49. a. R = 60.8 m
b. R = 137.8 m
51. a. vy2 = v0y2 − 2gy \(\Rightarrow\) y = 2.9 m/s
y = 3.3 m/s
y = \(\frac{v_{0y}^{2}}{2g}\) = \(\frac{(v_{0} \sin \theta)^{2}}{2g} \Rightarrow \sin \theta\) = 0.91 \(\Rightarrow\) \(\theta\) = 65.5°
53. R = 18.5 m
55. y = (tan\(\theta_{0}\))x − \(\Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big]\)x2 \(\Rightarrow\) v0 = 16.4 m/s
57. R = \(\frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \Rightarrow \theta_{0}\) = 15.0°
59. It takes the wide receiver 1.1 s to cover the last 10 m of his run.
Ttof = \(\frac{2(v_{0} \sin \theta)}{g} \Rightarrow \sin \theta\) = 0.27 \(\Rightarrow \theta\) = 15.6°
61. aC = 40 m/s2
63. aC = \(\frac{v^{2}}{r} \Rightarrow\) v2 = r, aC = 78.4, v = 8.85 m/s
T = 5.68 s, which is 0.176 rev/s = 10.6 rev/min
65. Venus is 108.2 million km from the Sun and has an orbital period of 0.6152 y.
r = 1.082 x 1011 m, T = 1.94 x 107 s
v = 3.5 x 104 m/s, aC = 1.135 x 10−2 m/s2
67. 360 rev/min = 6 rev/s
v = 3.8 m/s, aC = 144. m/s2
69. a. O′(t) = (4.0 \(\hat{i}\) + 3.0 \(\hat{j}\) + 5.0 \(\hat{k}\))t m
b. \(\vec{r}_{PS}\) = \(\vec{r}_{PS'}\) + \(\vec{r}_{S'S}\), \(\vec{r}\)(t) = \(\vec{r′}\)(t) + (4.0 \(\hat{i}\) + 3.0 \(\hat{j}\) + 5.0 \(\hat{k}\))t m
c. \(\vec{v}\)(t) = \(\vec{v′}\)(t) + (4.0 \(\hat{i}\) + 3.0 \(\hat{j}\) + 5.0 \(\hat{k}\)) m/s
d. The accelerations are the same.
71. \(\vec{v}_{PC}\) = (2.0 \(\hat{i}\) + 5.0 \(\hat{j}\) + 4.0 \(\hat{k}\))m/s
73. a. A = air, S = seagull, G = ground
\(\vec{v}_{SA}\) = 9.0 m/s, velocity of seagull with respect to still air
\(\vec{v}_{AG}\) = ?, \(\vec{v}_{SG}\) = 5 m/s, \(\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{AG} = \vec{v}_{SG} − \vec{v}_{SA}\)
\(\vec{v}_{AG}\) = −4.0 m/s
b. \(\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{SG}\) = −13.0 m/s
\(\frac{−6000\; m}{−13.0\; m/s}\) = 7 min 42 s
75. Take the positive direction to be the same direction that the river is flowing, which is east. S = shore/Earth, W = water, and B = boat.
a. \(\vec{v}_{BS}\) = 11 km/h, t = 8.2 min
b. \(\vec{v}_{BS}\) = −5 km/h, t = 18 min
c. \(\vec{v}_{BS} = \vec{v}_{BW} + \vec{v}_{WS}, \theta\) = 22° west of north
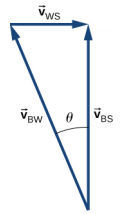
d. |\(\vec{v}_{BS}\)| = 7.4 km/h, t = 6.5 min
e. \(\vec{v}_{BS}\) = 8.54 km/h, but only the component of the velocity straight across the river is used to get the time
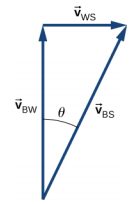
t = 6.0 min
Downstream = 0.3 km
77. \(\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}\)
|\(\vec{v}_{AC}\)| = 25 km/h, |\(\vec{v}_{CG}\)| = 15 km/h, |\(\vec{v}_{AG}\)| = 29.15 km/h, \(\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}\)
The angle between \(\vec{v}_{AC}\) and \(\vec{v}_{AG}\) is 31°, so the direction of the wind is 14° north of east.
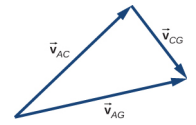
Additional Problems
79. aC = 39.6 m/s2
81. 90.0 km/h = 25.0 m/s, 9.0 km/h = 2.5 m/s, 60.0 km/h = 16.7 m/s
aT = −2.5 m/s2, aC = 1.86 m/s2, a = 3.1 m/s2
83. The radius of the circle of revolution at latitude \(\lambda\) is RE cos \(\lambda\). The velocity of the body is \(\frac{2 \pi r}{T}\). aC = \(\frac{4 \pi^{2} R_{E} \cos \lambda}{T^{2}}\) for \(\lambda\) = 40°, aC = 0.26% g
85. aT = 3.00 m/s2
v(5 s) = 15.00 m/s, aC = 150.00 m/s2, \(\theta\) = 88.8° with respect to the tangent to the circle of revolution directed inward.
|\(\vec{a}\)| = 150.03 m/s2
87. \(\vec{a}\)(t) = −A\(\omega^{2}\) cos \(\omega\)t \(\hat{i}\) − A\(\omega^{2}\) sin \(\omega\)t \(\hat{j}\)
aC = 5.0 m\(\omega^{2}\), \(\omega\) = 0.89 rad/s
\(\vec{v}\)(t) = −2.24 m/s \(\hat{i}\) − 3.87 m/s \(\hat{j}\)
89. \(\vec{r}_{1}\) = 1.5 \(\hat{j}\) + 4.0 \(\hat{k}\), \(\vec{r}_{2} = \Delta \vec{r} + \vec{r}_{1}\) = 2.5 \(\hat{i}\) + 4.7 \(\hat{j}\) + 2.8 \(\hat{k}\)
91. vx(t) = 265.0 m/s, vy(t) = 20.0 m/s, \(\vec{v}\)(5.0 s) = (265.0 \(\hat{i}\) + 20.0 \(\hat{j}\))m/s
93. R = 1.07 m
95. v0 = 20.1 m/s
97. v = 3072.5 m/s, aC = 0.223 m/s2
Challenge Problems
99. a. −400.0 m = v0yt − 4.9t2, 359.0 m = v0xt, t = \(\frac{359.0}{v_{0x}}\) − 400.0 = 359.0\(\frac{v_{0y}}{v_{0x}}\) − 4.9\(\left(\dfrac{359.0}{v_{0x}}\right)^{2}\)
−400.0 = 359.0 tan 40 − \(\frac{631,516.9}{v_{0x}^{2}} \Rightarrow\) v0x2 = 900.6, v0x = 30.0 m/s, v0y = v0x tan 40 = 25.2 m/s, v = 39.2 m/s
b. t = 12.0 s
101. a. \(\vec{r}_{TC}\) = (−32 + 80t) \(\hat{i}\) + 50t \(\hat{j}\), |\(\vec{r}_{TC}\)|2 = (−32 + 80t)2 + (50t)2
2r\(\frac{dr}{dt}\) = 2(−32 + 80t) + 100t, \(\frac{dr}{dt} = \frac{2(−32 + 80t) + 100t}{2r}\) = 0
260t = 64 \(\Rightarrow\) t = 15 min
b. |\(\vec{r}_{TC}\)| = 17 km


