7.23: Zeeman effect with nuclear spin
- Page ID
- 8924
So far, I have described the splitting of the states within a level \(J\) on the assumption that there is no nuclear spin. Now I move to the case of an atom with nuclear spin \(I\). We have seen in section 7.18, equation 7.18.1, that the electronic angular momentum \(\textbf{J}\) combines with the nuclear spin angular momentum \(\textbf{I}\) to form the total angular momentum \(\textbf{F}\) for the atom, and we have seen, in equation 7.18.2, how the term values of the resulting hyperfine levels are spaced. Let us consider a level \(J=1\) in an atom whose nuclear spin is \(I = 1\). The hyperfine levels are then spaced in exactly the same manner as the levels are placed in a \(^3 \text{P}\) term (\(L = 1\), \(S = 1\)). Draw the three hyperfine levels on your graph paper, with the \(F = 0, \ 1, \ 2\) hyperfine levels at \(−0.2, \ −0.1\) and \(+0.1\) inches respectively. Now, if you apply a very small magnetic field, each hyperfine level will be split up into \(2F+1\) equally-spaced states. But you must now bear in mind that the coupling between \(\textbf{J}\) and \(\textbf{I}\) is exceedingly weak (i.e. the spacings between the hyperfine levels is exceedingly small), so this Zeeman effect will obtain for only very tiny magnetic fields indeed. As soon as the magnetic field is at all appreciable, \(\textbf{J}\) and \(\textbf{I}\) uncouple from each other and they then couple independently with \(\textbf{B}\) to form a Paschen-Back effect. Does this make life unbearably complicated? As it turns out - not at all! The separation of the states is given by exactly the same sort of expression as for the Paschen-Back effect earlier described, namely \((M_J + g_I M_I) \mu_B B + AM_J M_I\), except that the nuclear \(g\)-factor is not \(2\) as in the case of the electron, but is of order \(10^{-3}\). This makes a world of difference to the way the states are separated. Let us calculate the term values, as we did before with the Paschen-Back effect, and we'll use the same field strength as before so that \(\mu_B B\) is represented by \(4\) inches, but this time, purely for illustrative purposes, we'll put \(g_I = 0.002\) and \(A = 0.0002\) inches. The result of the calculation (which you should carry out yourself - it is very quick with a programmable calculator, though tedious without) is as follows:
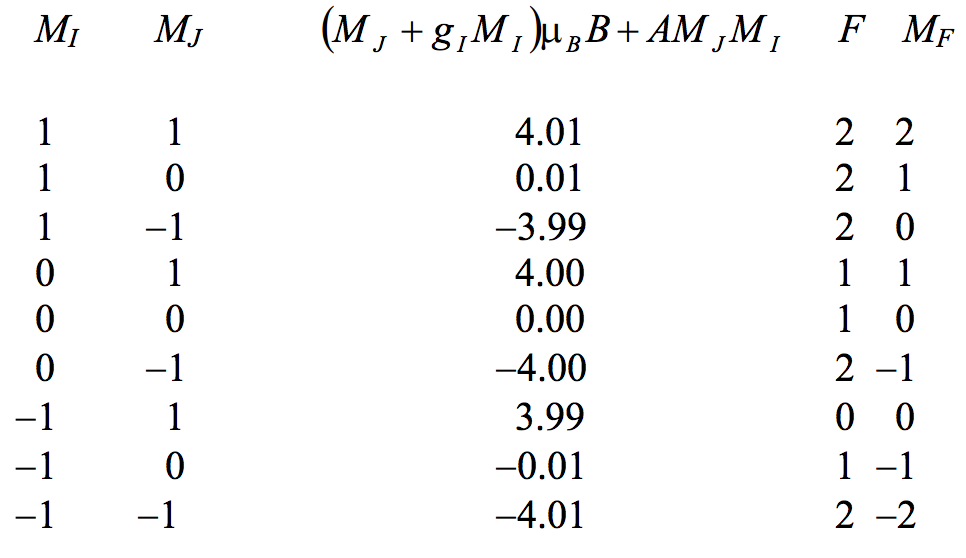
Now please do draw these out on your graph paper. You will find that the states are spaced in three widely-separated groups of three, with three closely-separated states in each group. You will not appreciate exactly what is happening unless you actually draw it out. But , if you do, you will see that, if your resolution is such that you cannot resolve the hyperfine structure in the zero-field situation, and you are unaware of or do not care about the nuclear spin, and you think that you have but a single level with \(J = 1\), when you apply a magnetic field what happens is this: you will find that this level is apparently split into three "states" (which you cannot resolve into their several genuine states), and it will appear that you have a perfectly ordinary Zeeman effect in which the nuclear spin plays no role at all. Only with high-resolution, cold-source, interferometric resolution will you see the hyperfine structure of each component into hyperfine components.


