18.2: Vectors
- Page ID
- 7941
Check Your Understanding
2.1. a. Not equal because they are orthogonal; b. not equal because they have different magnitudes; c. not equal because they have different magnitudes and directions; d. not equal because they are antiparallel; e. equal.
2.2. 16 m; \(\vec{D}\) = −16 m \(\hat{u}\)
2.3. G = 28.2 cm, \(\theta_{G}\) = 291°
2.4. \(\vec{D}\) = (−5.0 \(\hat{i}\) − 3.0 \(\hat{j}\))cm; the fly moved 5.0 cm to the left and 3.0 cm down from its landing site.
2.5. 5.83 cm, 211°
2.6. \(\vec{D}\) = (−20 m) \(\hat{j}\)
2.7. 35.1 m/s = 126.4 km/h
2.8. \(\vec{G}\) = (10.25 \(\hat{i}\) − 26.22 \(\hat{j}\))cm
2.9. D = 55.7 N; direction 65.7° north of east
2.10. \(\hat{v}\) = 0.8 \(\hat{i}\) + 0.6 \(\hat{j}\), 36.87° north of east
2.11. \(\vec{A} \cdotp \vec{B}\) = −57.3, \(\vec{F} \cdotp \vec{C}\) = 27.8
2.13. 131.9°
2.14. W1 = 1.5 J, W2 = 0.3 J
2.15. \(\vec{A} \times \vec{B}\) = −40.1 \(\hat{k}\) or, equivalently, |\(\vec{A} \times \vec{B}\)| = 40.1, and the direction is into the page; \(\vec{C} \times \vec{F}\) = + 157.6 \(\hat{k}\) or, equivalently, |\(\vec{C} \times \vec{F}\)| = 157.6, and the direction is out of the page.
2.16. a. −2 \(\hat{k}\), b. 2, c. 153.4°, d. 135°
Conceptual Questions
1. Scalar
3. Answers may vary
5. Parallel, sum of magnitudes, antiparallel, zero
7. Yes, yes
9. Zero, yes
11. No
13. Equal, equal, the same
15. A unit vector of the x-axis
17. They are equal.
19. Yes
21. a. C = \(\vec{A} \cdotp \vec{B}\), b. \(\vec{C} = \vec{A} \times \vec{B}\) or \(\vec{C} = \vec{A} - \vec{B}\), c. \(\vec{C} = \vec{A} \times\vec{B}\), d. \(\vec{C}\) = A\(\vec{B}\), e. \(\vec{C} + 2 \vec{A} = \vec{B}\), f. \(\vec{C} = \vec{A} \times \vec{B}\), g. left side is a scalar and right side is a vector, h. \(\vec{C} = 2 \vec{A} \times \vec{B}\), i. \(\vec{C} = \frac{\vec{A}}{B}\), j. \(\vec{C} = \frac{\vec{A}}{B}\)
23. They are orthogonal.
Problems
25. \(\vec{h}\) = −16.4 m \(\hat{u}\), 16.4 m
27. 30.8 m, 35.7° west of north
29. 134 km, 80°
31. 7.34 km, 63.5° south of east
33. 3.8 km east, 3.2 km north, 7.0 km
35. 14.3 km, 65°
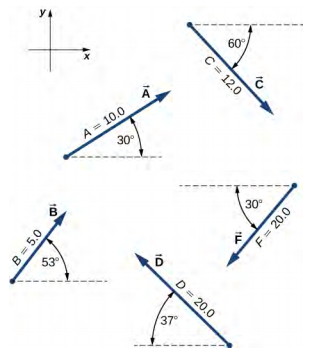
37. a. \(\vec{A}\) = + 8.66 \(\hat{i}\) + 5.00 \(\hat{j}\)
b. \(\vec{B}\) = + 3.01 \(\hat{i}\) + 3.99 \(\hat{j}\)
c. \(\vec{C}\) = + 6.00 \(\hat{i}\) − 10.39 \(\hat{j}\)
d. \(\vec{D}\) = −15.97 \(\hat{i}\) + 12.04 \(\hat{j}\)
f. \(\vec{F}\) = −17.32 \(\hat{i}\) − 10.00 \(\hat{j}\)
39. a. 1.94 km, 7.24 km
b. proof
41. 3.8 km east, 3.2 km north, 2.0 km, \(\vec{D}\) = (3.8 \(\hat{i}\) + 3.2 \(\hat{j}\))km
43. P1(2.165 m, 1.250 m), P2(−1.900 m, 3.290 m), 5.27 m
45. 8.60 m, A(2\(\sqrt{5}\) m, 0.647\(\pi\)), B(3\(\sqrt{2}\) m, 0.75\(\pi\))
47. a. \(\vec{A} + \vec{B}\) = −4 \(\hat{i}\) − 6 \(\hat{j}\), |\(\vec{A} + \vec{B}\)| = 7.211, \(\theta\) = 236.3°
b. \(\vec{A} -\vec{B}\) = -2 \(\hat{i}\) + 2 \(\hat{j}\), |\(\vec{A} - \vec{B}\)| = 2\(\sqrt{2}\), \(\theta\) = 135°
49. a. \(\vec{C}\) = (5.0 \(\hat{i}\) − 1.0 \(\hat{j}\) − 3.0 \(\hat{k}\))m, C = 5.92 m
b. \(\vec{D}\) = (4.0 \(\hat{i}\) − 11.0 \(\hat{j}\) + 15.0 \(\hat{k}\))m, D = 19.03 m
51. \(\vec{D}\) = (3.3 \(\hat{i}\) − 6.6 \(\hat{j}\))km, \(\hat{i}\) is to the east, 7.34 km, −63.5°
53. a. \(\vec{R}\) = −1.35 \(\hat{i}\) − 22.04 \(\hat{j}\)
b. \(\vec{R}\) = −17.98 \(\hat{i}\) + 0.89 \(\hat{j}\)
55. \(\vec{D}\) = (200 \(\hat{i}\) + 300 \(\hat{j}\))yd, D = 360.5 yd, 56.3° north of east; The numerical answers would stay the same but the physical unit would be meters. The physical meaning and distances would be about the same because 1 yd is comparable with 1 m.
57. \(\vec{R}\) = −3 \(\hat{i}\) − 16 \(\hat{j}\)
59. \(\vec{E}\) = E \(\hat{E}\), Ex = + 178.9 V/m , Ey = −357.8 V/m, Ez = 0.0 V/m, \(\theta_{E}\) = −tan−1(2)
61. a. \(\vec{R}_{B}\) = (12.278 \(\hat{i}\) + 7.089 \(\hat{j}\) + 2.500 \(\hat{k}\))km, \(\vec{R}_{D}\) = (−0.262 \(\hat{i}\) + 3.000 \(\hat{k}\))km
b. |\(\vec{R}_{B} − \vec{R}_{D}\)| = 14.414 km
63. a. 8.66
b. 10.39
c. 0.866
d. 17.32
65. \(\theta_{i}\) = 64.12°, \(\theta_{j}\) = 150.79°, \(\theta_{k}\) = 77.39°
67. a. −119.98 \(\hat{k}\)
b. 0 \(\hat{k}\)
c. +93.69 \(\hat{k}\)
d. −240.0 \(\hat{k}\)
e. +3.993 \(\hat{k}\)
f. −3.009 \(\hat{k}\)
g. +14.99 \(\hat{k}\)
h. 0
69. a. 0
b. 173,194
c. +199,993 \(\hat{k}\)
Additional Problems
71. a. 18.4 km and 26.2 km
b. 31.5 km and 5.56 km
73. a. (r, \(\phi + \frac{\pi}{2}\))
b. (2r, \(\phi + 2 \pi\))
c. (3r, −\(\phi\))
75. dPM = 33.12 nmi = 61.34 km, dNP = 35.47 nmi = 65.69 km
77. proof
79. a. 10.00 m
b. 5\(\pi\) m, c. 0
81. 22.2 km/h, 35.8° south of west
83. 240.2 m, 2.2° south of west
85. \(\vec{B}\) = −4.0 \(\hat{i}\) + 3.0 \(\hat{j}\) or \(\vec{B}\) = 4.0 \(\hat{i}\) − 3.0 \(\hat{j}\)
87. proof
Challenge Problems
89. G\(\perp\) = 2375\(\sqrt{17}\) ≈ 9792
91. proof
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


