18.5: Newton's Laws of Motion
- Page ID
- 7944
Check Your Understanding
5.1. 14 N, 56° measured from the positive x-axis
5.2. a. His weight acts downward, and the force of air resistance with the parachute acts upward. b. neither; the forces are equal in magnitude
5.3. 0.1 m/s2
5.4. 40 m/s2
5.5. a. 159.0 \(\hat{i}\) + 770.0 \(\hat{j}\) N; b. 0.1590 \(\hat{i}\) + 0.7700 \(\hat{j}\) N
5.6. a = 2.78 m/s2
5.7. a. 3.0 m/s2; b. 18 N
5.8. a. 1.7 m/s2; b. 1.3 m/s2
5.9. 6.0 × 102 N
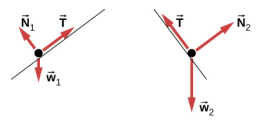
5.10.
Conceptual Questions
1. Forces are directional and have magnitude.
3. The cupcake velocity before the braking action was the same as that of the car. Therefore, the cupcakes were unrestricted bodies in motion, and when the car suddenly stopped, the cupcakes kept moving forward according to Newton’s first law.
5. No. If the force were zero at this point, then there would be nothing to change the object’s momentary zero velocity. Since we do not observe the object hanging motionless in the air, the force could not be zero.
7. The astronaut is truly weightless in the location described, because there is no large body (planet or star) nearby to exert a gravitational force. Her mass is 70 kg regardless of where she is located.
9. The force you exert (a contact force equal in magnitude to your weight) is small. Earth is extremely massive by comparison. Thus, the acceleration of Earth would be incredibly small. To see this, use Newton’s second law to calculate the acceleration you would cause if your weight is 600.0 N and the mass of Earth is 6.00 x 1024 kg.
11. a. action: Earth pulls on the Moon, reaction: Moon pulls on Earth; b. action: foot applies force to ball, reaction: ball applies force to foot; c. action: rocket pushes on gas, reaction: gas pushes back on rocket; d. action: car tires push backward on road, reaction: road pushes forward on tires; e. action: jumper pushes down on ground, reaction: ground pushes up on jumper; f. action: gun pushes forward on bullet, reaction: bullet pushes backward on gun.
13. a. The rifle (the shell supported by the rifle) exerts a force to expel the bullet; the reaction to this force is the force that the bullet exerts on the rifle (shell) in opposite direction. b. In a recoilless rifle, the shell is not secured in the rifle; hence, as the bullet is pushed to move forward, the shell is pushed to eject from the opposite end of the barrel. c. It is not safe to stand behind a recoilless rifle.
15. a. Yes, the force can be acting to the left; the particle would experience deceleration and lose speed. b. Yes, the force can be acting downward because its weight acts downward even as it moves to the right.
17. Two forces of different types: weight acting downward and normal force acting upward
Problems
19. a. \(\vec{F}_{net}\) = 5.0 \(\hat{i}\) + 10.0 \(\hat{j}\) N
b. The magnitude is Fnet = 11 N, and the direction is \(\theta\) = 63°
21. a. \(\vec{F}_{net}\) = 660.0 \(\hat{i}\) + 150.0 \(\hat{j}\) N
b. Fnet = 676.6 N at \(\theta\) = 12.8° from David’s rope
23. a. \(\vec{F}_{net}\) = 95.0 \(\hat{i}\) + 283 \(\hat{j}\) N
b. 299 N at 71° north of east
c. \(\vec{F}_{DS}\) = − (95.0 \(\hat{i}\) + 283 \(\hat{j}\)) N
25. Running from rest, the sprinter attains a velocity of v = 12.96 m/s, at end of acceleration. We find the time for acceleration using x = 20.00 m = 0 + 0.5at12, or t1 = 3.086 s. For maintained velocity, x2 = vt2, or t2 = \(\frac{x_{2}}{v}\) = \(\frac{80.00\; m}{12.96\; m/s}\) = 6.173 s. Total time = 9.259 s.
27. a. m = 56.0 kg
b. ameas = aastro + aship, where aship = \(\frac{m_{astro} a_{astro}}{m_{ship}}\)
c. If the force could be exerted on the astronaut by another source (other than the spaceship), then the spaceship would not experience a recoil.
29. Fnet = 4.12 x 105 N
31. a = 253 m/s2
33. Fnet = F − f = ma \(\Rightarrow\) F = 1.26 x 103 N
35. v2 = v02 + 2ax \(\Rightarrow\) a = −7.80 m/s2, Fnet = −7.80 x 103 N
37. a. \(\vec{F}_{net}\) = m\(\vec{a} \Rightarrow \vec{a}\) = 9.0 \(\hat{i}\) m/s2
b. The acceleration has magnitude 9.0 m/s2, so x = 110 m.
39. 1.6 \(\hat{i}\) − 0.8 \(\hat{j}\) m/s2
41. a. wMoon = mgMoon, m = 150 kg, wEarth = 1.5 x 103 N
b. Mass does not change, so the suited astronaut’s mass on both Earth and the Moon is 150 kg.
43. a. Fh = 3.68 x 103 N and w = 7.35 x 102 N, \(\frac{F_{h}}{w}\) = 5.00 times greater than weight
b. Fnet = 3750 N, \(\theta\) = 11.3° from horizontal
45. w = 19.6 N, Fnet = 5.40 N, Fnet = ma \(\Rightarrow\) a = 2.70 m/s2
47. 98 N
49. 497 N
51. a. Fnet= 2.64 x 107 N
b. The force exerted on the ship is also 2.64 x 107 N because it is opposite the shell’s direction of motion.
53. Because the weight of the history book is the force exerted by Earth on the history book, we represent it as \(\vec{F}_{EH}\) = −14 \(\hat{j}\) N. Aside from this, the history book interacts only with the physics book. Because the acceleration of the history book is zero, the net force on it is zero by Newton’s second law: \(\vec{F}_{PH} + \vec{F}_{EH} = \vec{0}\), where \(\vec{F}_{PH}\) is the force exerted by the physics book on the history book. Thus, \(\vec{F}_{PH} = − \vec{F}_{EH} = −(−14\; \hat{j})\; N = 14\; \hat{j}\; N\). We find that the physics book exerts an upward force of magnitude 14 N on the history book. The physics book has three forces exerted on it: \(\vec{F}_{EP}\) due to Earth, \(\vec{F}_{HP}\) due to the history book, and \(\vec{F}_{DP}\) due to the desktop. Since the physics book weighs 18 N, \(\vec{F}_{EP} = −18\; \hat{j}\; N\). From Newton’s third law, \(\vec{F}_{HP} = − \vec{F}_{PH}\), so \(\vec{F}_{HP} = −14\; \hat{j}\; N\). Newton’s second law applied to the physics book gives \(\Sigma \vec{F} = \vec{0}\), or \(\vec{F}_{DP} + \vec{F}_{EP} + \vec{F}_{HP} = \vec{0}\), so \(\vec{F}_{DP}\) = −(−18 \(\hat{j}\)) − (−14 \(\hat{j}\)) = 32 \(\hat{j}\) N. The desk exerts an upward force of 32 N on the physics book. To arrive at this solution, we apply Newton’s second law twice and Newton’s third law once.
55. a. The free-body diagram of the pulley closest to the foot:
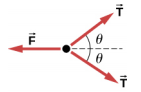
b. T = mg, F = 2T cos \(\theta\) = 2mg cos \(\theta\)
57. a. 1.95 m/s2
b. 1960 N
59. a. T = 1.96 x 10−4 N
b. T′ = 4.71 x 10−4 N, \(\frac{T′}{T}\) = 2.40 times the tension in the vertical strand
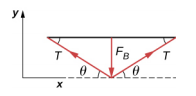
61. \[\begin{split} F_{y\; net} = F_{\perp} - 2T \sin \theta & = 0 \\ F_{\perp} & = 2T \sin \theta \\ T & = \frac{F_{\perp}}{2 \sin \theta} \end{split}\]
63. a. see Example 5.13
b. 1.5 N
c. 15 N
65. a. 5.6 kg
b. 55 N
c. T2 = 60 N
d.
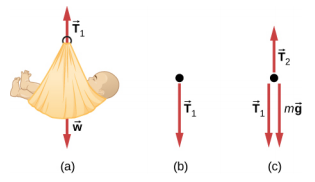
67. a. 4.9 m/s2, 17 N
b. 9.8 N
69.
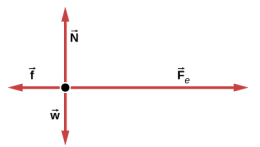
71.
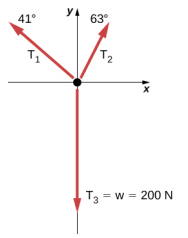
Additional Problems
73. 5.90 kg
75.
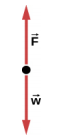
77. a. Fnet = \(\frac{m(v^{2} - v_{0}^{2})}{2x}\)
b. 2590 N
79. \[\begin{split} \vec{F}_{net} & = 6.02\; \hat{i} + 14.0\; \hat{j}\; N \\ \vec{F}_{net} & = m \vec{a} \Rightarrow \vec{a} = 0.602\; \hat{i} + 1.40\; \hat{j}\; m/s^{2} \end{split}\]
81. \[\begin{split} \vec{F}_{net} & = \vec{F}_{A} + \vec{F}_{B} \\ \vec{F}_{net} & = A \hat{i} + (-1.1A\; \hat{i} - 1.41A\; \hat{j}) \\ \vec{F}_{net} & = A(-0.41\; \hat{i} - 1.41\; \hat{j}) \end{split}\]
\(\theta\) = 254° (We add 180°, because the angle is in quadrant IV.)
83. \(F = 2mk^{2}x^{2}\); First, take the derivative of the velocity function to obtain \(a = 2kxv = 2kx(kx^2) = 2k^{2}x^{3}\). Then apply Newton’s second law \(F = ma = 2mk^{2}x^{2}\).
85. a. For box A, NA = mg and NB = mg cos \(\theta\)
b. NA > NB because for \(\theta\) < 90°, cos \(\theta\) < 1
c. NA > NB when \(\theta\) = 10°
87. a. 8.66 N
b. 0.433 m
89. 0.40 or 40%
91. 16 N
Challenge Problems
93. a.
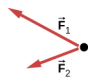
b. No; \(\vec{F}_{R}\) is not shown, because it would replace \(\vec{F}_{1}\) and \(\vec{F}_{2}\). (If we want to show it, we could draw it and then place squiggly lines on \(\vec{F}_{1}\) and \(\vec{F}_{2}\) to show that they are no longer considered.
95. a. 14.1 m/s
b. 601 N
97. \(\frac{F}{m}\)t2
99. 936 N
101. \(\vec{a}\) = −248 \(\hat{i}\) − 433 \(\hat{j}\) m/s2
103. 0.548 m/s2
105. a. T1 = \(\frac{2mg}{\sin \theta}\), T2 = \(\frac{mg}{\sin (\arctan(\frac{1}{2} \tan \theta))}\), T3 = \(\frac{2mg}{\tan \theta}\)
b. \(\phi = \arctan(\frac{1}{2} \tan \theta)\)
c. 2.56°
d. x = d(2 cos \(\theta\) + 2 cos(arctan(\(\frac{1}{2}\) tan \(\theta\))) + 1)
107. a. \(\vec{a}\) = (5.00 m \(\hat{i}\) + 3.00 m \(\hat{j}\)) m/s2
b. 1.38 kg
c. 21.2 m/s
d. \(\vec{v}\) = (18.1 \(\hat{i}\) + 10.9 \(\hat{j}\)) m/s2
109. a. 0.900 \(\hat{i}\) + 0.600 \(\hat{j}\) N
b. 1.08 N
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


