6.4: Applying Gauss’s Law
- Page ID
- 4381
By the end of this section, you will be able to:
- Explain what spherical, cylindrical, and planar symmetry are
- Recognize whether or not a given system possesses one of these symmetries
- Apply Gauss’s law to determine the electric field of a system with one of these symmetries
Gauss’s law is very helpful in determining expressions for the electric field, even though the law is not directly about the electric field; it is about the electric flux. It turns out that in situations that have certain symmetries (spherical, cylindrical, or planar) in the charge distribution, we can deduce the electric field based on knowledge of the electric flux. In these systems, we can find a Gaussian surface S over which the electric field has constant magnitude. Furthermore, if \(\vec{E}\) is parallel to \(\hat{n}\) everywhere on the surface, then \(\vec{E} \cdot \hat{n} = E\). (If \(\vec{E}\) and \(\hat{n}\) are antiparallel everywhere on the surface, \(\vec{E} \cdot \hat{n} = - E\).) Gauss’s law then simplifies to
\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = E \oint_S dA = EA = \dfrac{q_{enc}}{\epsilon_0},\]
where A is the area of the surface. Note that these symmetries lead to the transformation of the flux integral into a product of the magnitude of the electric field and an appropriate area. When you use this flux in the expression for Gauss’s law, you obtain an algebraic equation that you can solve for the magnitude of the electric field, which looks like
\[E \approx \dfrac{q_{enc}}{\epsilon_0 \, area}.\]
The direction of the electric field at point P is obtained from the symmetry of the charge distribution and the type of charge in the distribution. Therefore, Gauss’s law can be used to determine \(\vec{E}\). Here is a summary of the steps we will follow:
- Identify the spatial symmetry of the charge distribution. This is an important first step that allows us to choose the appropriate Gaussian surface. As examples, an isolated point charge has spherical symmetry, and an infinite line of charge has cylindrical symmetry.
- Choose a Gaussian surface with the same symmetry as the charge distribution and identify its consequences. With this choice, \(\vec{E} \cdot \hat{n}\) is easily determined over the Gaussian surface.
- Evaluate the integral \(\oint_S \vec{E} \cdot \hat{n} dA\) over the Gaussian surface, that is, calculate the flux through the surface. The symmetry of the Gaussian surface allows us to factor \(\vec{E} \cdot \hat{n}\) outside the integral.
- Determine the amount of charge enclosed by the Gaussian surface. This is an evaluation of the right-hand side of the equation representing Gauss’s law. It is often necessary to perform an integration to obtain the net enclosed charge.
- Evaluate the electric field of the charge distribution. The field may now be found using the results of steps 3 and 4.
Basically, there are only three types of symmetry that allow Gauss’s law to be used to deduce the electric field. They are
- A charge distribution with spherical symmetry
- A charge distribution with cylindrical symmetry
- A charge distribution with planar symmetry
To exploit the symmetry, we perform the calculations in appropriate coordinate systems and use the right kind of Gaussian surface for that symmetry, applying the remaining four steps.
Charge Distribution with Spherical Symmetry
A charge distribution has spherical symmetry if the density of charge depends only on the distance from a point in space and not on the direction. In other words, if you rotate the system, it doesn’t look different. For instance, if a sphere of radius R is uniformly charged with charge density \(\rho_0\) then the distribution has spherical symmetry (Figure \(\PageIndex{1a}\)). On the other hand, if a sphere of radius R is charged so that the top half of the sphere has uniform charge density \(\rho_1\) and the bottom half has a uniform charge density \(\rho_2 \neq \rho_1\) then the sphere does not have spherical symmetry because the charge density depends on the direction (Figure \(\PageIndex{1b}\)). Thus, it is not the shape of the object but rather the shape of the charge distribution that determines whether or not a system has spherical symmetry.
Figure \(\PageIndex{1c}\) shows a sphere with four different shells, each with its own uniform charge density. Although this is a situation where charge density in the full sphere is not uniform, the charge density function depends only on the distance from the center and not on the direction. Therefore, this charge distribution does have spherical symmetry.
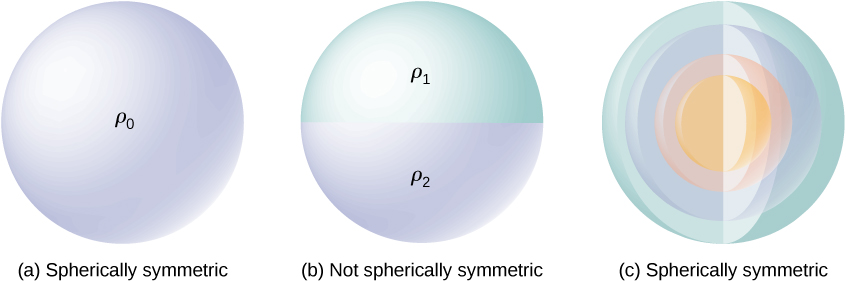
One good way to determine whether or not your problem has spherical symmetry is to look at the charge density function in spherical coordinates, \(\rho(r, \theta, \phi)\). If the charge density is only a function of r, that is \(\rho = \rho(r)\), then you have spherical symmetry. If the density depends on \(\theta\) or \(\phi\), you could change it by rotation; hence, you would not have spherical symmetry.
Consequences of symmetry
In all spherically symmetrical cases, the electric field at any point must be radially directed, because the charge and, hence, the field must be invariant under rotation. Therefore, using spherical coordinates with their origins at the center of the spherical charge distribution, we can write down the expected form of the electric field at a point P located at a distance r from the center:
\[Spherical \, symmetry: \, \vec{E}_p = E_p(r)\hat{r},\]
where \(\hat{r}\) is the unit vector pointed in the direction from the origin to the field point P. The radial component \(E_p\) of the electric field can be positive or negative. When \(E_p > 0\), the electric field at P points away from the origin, and when \(E_p < 0\), the electric field at P points toward the origin.
Gaussian surface and flux calculations
We can now use this form of the electric field to obtain the flux of the electric field through the Gaussian surface. For spherical symmetry, the Gaussian surface is a closed spherical surface that has the same center as the center of the charge distribution. Thus, the direction of the area vector of an area element on the Gaussian surface at any point is parallel to the direction of the electric field at that point, since they are both radially directed outward (Figure \(\PageIndex{2}\)).
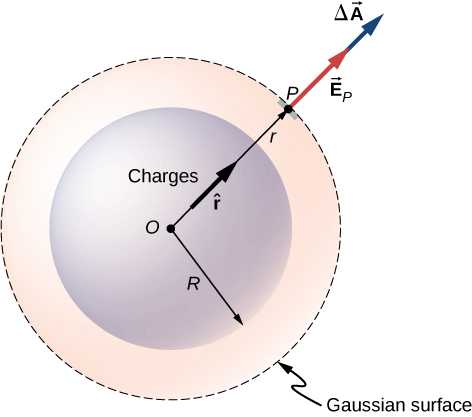
The magnitude of the electric field \(\vec{E}\) must be the same everywhere on a spherical Gaussian surface concentric with the distribution. For a spherical surface of radius r:
\[\Phi = \oint_S \vec{E}_p \cdot \hat{n} dA = E_p \oint_S dA = E_p \, 4\pi r^2.\]
Using Gauss’s law
According to Gauss’s law, the flux through a closed surface is equal to the total charge enclosed within the closed surface divided by the permittivity of vacuum \(\epsilon_0\). Let \(q_{enc}\) be the total charge enclosed inside the distance r from the origin, which is the space inside the Gaussian spherical surface of radius r. This gives the following relation for Gauss’s law:
\[4\pi r^2 E = \dfrac{q_{enc}}{\epsilon_0}.\]
Hence, the electric field at point P that is a distance r from the center of a spherically symmetrical charge distribution has the following magnitude and direction:
\[Magnitude: \, E(r) = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{enc}}{r^2}\]
Direction: radial from O to P or from P to O.
The direction of the field at point P depends on whether the charge in the sphere is positive or negative. For a net positive charge enclosed within the Gaussian surface, the direction is from O to P, and for a net negative charge, the direction is from P to O. This is all we need for a point charge, and you will notice that the result above is identical to that for a point charge. However, Gauss’s law becomes truly useful in cases where the charge occupies a finite volume.
Computing Enclosed Charge
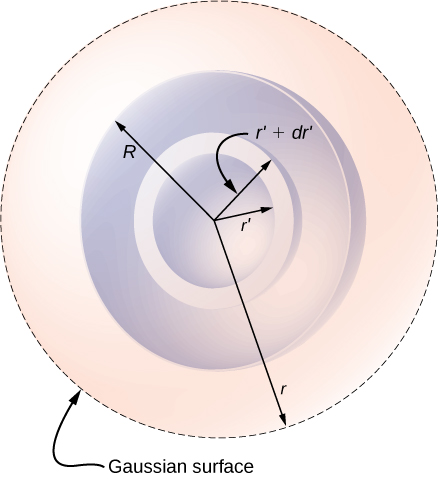
The more interesting case is when a spherical charge distribution occupies a volume, and asking what the electric field inside the charge distribution is thus becomes relevant. In this case, the charge enclosed depends on the distance r of the field point relative to the radius of the charge distribution R, such as that shown in Figure \(\PageIndex{3}\).
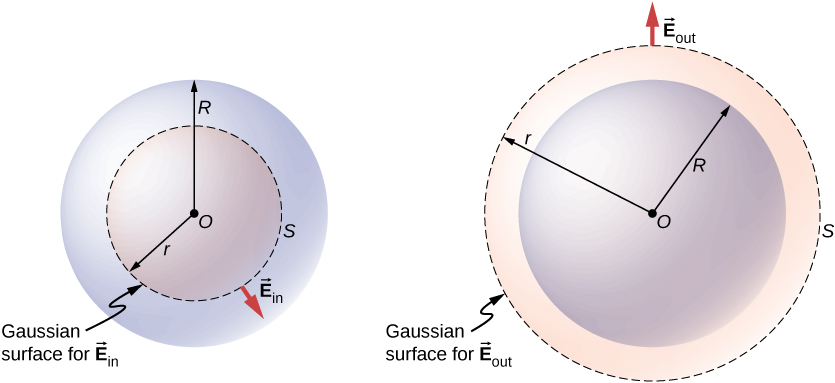
If point P is located outside the charge distribution—that is, if \(r \geq R\) —then the Gaussian surface containing P encloses all charges in the sphere. In this case, \(q_{enc}\) equals the total charge in the sphere. On the other hand, if point P is within the spherical charge distribution, that is, if \(r < R\), then the Gaussian surface encloses a smaller sphere than the sphere of charge distribution. In this case, \(q_{enc}\) is less than the total charge present in the sphere. Referring to Figure \(\PageIndex{3}\), we can write \(q_{enc}\) as
\[q_{enc} = q_{tot} (total \, charge) \, if \, r \geq R\]
\[q_{enc} = q_{within \, r < R} (only \, charge \, within \, r < R) \, if \, r < R\]
The field at a point outside the charge distribution is also called \(\vec{E}_{out}\), and the field at a point inside the charge distribution is called \(\vec{E}_{in}\). Focusing on the two types of field points, either inside or outside the charge distribution, we can now write the magnitude of the electric field as
\[P \, outside \, sphere \, E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}\]
\[P \, inside \, sphere \, E_{in} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{within \, r < R}}{r^2}.\]
Note that the electric field outside a spherically symmetrical charge distribution is identical to that of a point charge at the center that has a charge equal to the total charge of the spherical charge distribution. This is remarkable since the charges are not located at the center only. We now work out specific examples of spherical charge distributions, starting with the case of a uniformly charged sphere.
A sphere of radius R, such as that shown in Figure \(\PageIndex{3}\), has a uniform volume charge density \(\rho_0\). Find the electric field at a point outside the sphere and at a point inside the sphere.
Strategy
Apply the Gauss’s law problem-solving strategy, where we have already worked out the flux calculation.
Solution
The charge enclosed by the Gaussian surface is given by
\[q_{enc} = \int \rho_0 dV = \int_0^r \rho_0 4\pi r'^2 dr' = \rho \left(\dfrac{4}{3} \pi r^3\right).\]
The answer for electric field amplitude can then be written down immediately for a point outside the sphere, labeled \(E_{out}\) and a point inside the sphere, labeled \(E_{in}\).
\[E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}, \, q_{tot} = \dfrac{4}{3} \pi R^3 \, \rho_0,\]
\[E_{in} = \dfrac{q_{enc}}{4\pi \epsilon_0 r^2} = \dfrac{\rho_0r}{3 \epsilon_0}, \, since \, q_{enc} = \dfrac{4}{3} \pi r^3 \rho_0.\]
It is interesting to note that the magnitude of the electric field increases inside the material as you go out, since the amount of charge enclosed by the Gaussian surface increases with the volume. Specifically, the charge enclosed grows \(\propto r^3\), whereas the field from each infinitesimal element of charge drops off \(\propto 1/r^2\) with the net result that the electric field within the distribution increases in strength linearly with the radius. The magnitude of the electric field outside the sphere decreases as you go away from the charges, because the included charge remains the same but the distance increases. Figure \(\PageIndex{4}\) displays the variation of the magnitude of the electric field with distance from the center of a uniformly charged sphere.
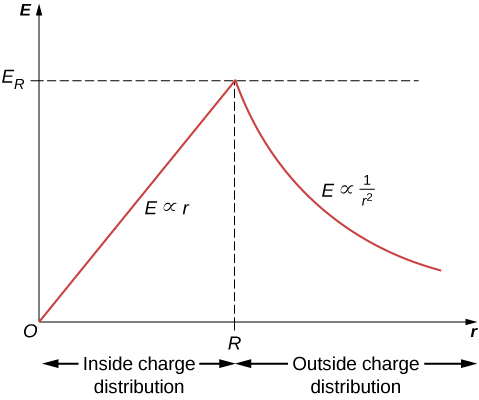
The direction of the electric field at any point P is radially outward from the origin if \(\rho_0\) is positive, and inward (i.e., toward the center) if \(\rho_0\) is negative. The electric field at some representative space points are displayed in Figure \(\PageIndex{5}\) whose radial coordinates r are \(r = R/2, \, r = R,\) and \(r = 2R\).
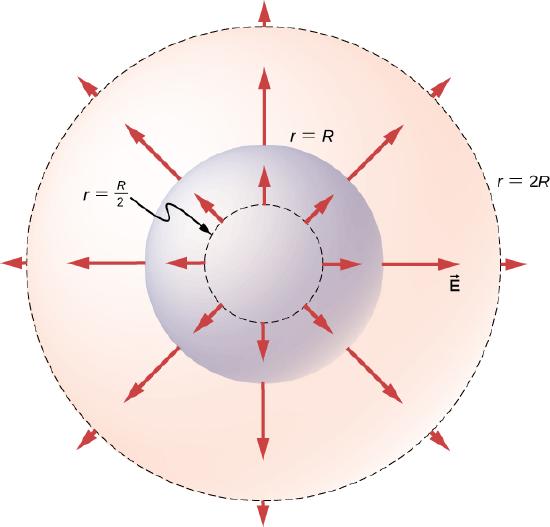
Significance
Notice that \(E_{out}\) has the same form as the equation of the electric field of an isolated point charge. In determining the electric field of a uniform spherical charge distribution, we can therefore assume that all of the charge inside the appropriate spherical Gaussian surface is located at the center of the distribution.
A non-conducting sphere of radius R has a non-uniform charge density that varies with the distance from its center as given by
\[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\]
where a is a constant. We require \(n \geq 0\) so that the charge density is not undefined at \(r = 0\). Find the electric field at a point outside the sphere and at a point inside the sphere.
Strategy
Apply the Gauss’s law strategy given above, where we work out the enclosed charge integrals separately for cases inside and outside the sphere.
Solution
Since the given charge density function has only a radial dependence and no dependence on direction, we have a spherically symmetrical situation. Therefore, the magnitude of the electric field at any point is given above and the direction is radial. We just need to find the enclosed charge \(q_{enc}\), which depends on the location of the field point.
A note about symbols: We use \(r'\) for locating charges in the charge distribution and r for locating the field point(s) at the Gaussian surface(s). The letter R is used for the radius of the charge distribution.
As charge density is not constant here, we need to integrate the charge density function over the volume enclosed by the Gaussian surface. Therefore, we set up the problem for charges in one spherical shell, say between \(r'\) and \(r' + dr'\) as shown in Figure \(\PageIndex{6}\). The volume of charges in the shell of infinitesimal width is equal to the product of the area of surface \(4\pi r'^2\) and the thickness \(dr'\). Multiplying the volume with the density at this location, which is \(ar'^n\), gives the charge in the shell:
\[dq = ar'^n 4\pi r'^2 dr'. \nonumber\]
(a) Field at a point outside the charge distribution. In this case, the Gaussian surface, which contains the field point P, has a radius r that is greater than the radius R of the charge distribution, \(r > R\). Therefore, all charges of the charge distribution are enclosed within the Gaussian surface. Note that the space between \(r' = R\) and \(r' = r\) is empty of charges and therefore does not contribute to the integral over the volume enclosed by the Gaussian surface:
\[q_{enc} = \int dq = \int_0^R ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} R^{n+3}. \nonumber\]
This is used in the general result for \(E_{out}\) above to obtain the electric field at a point outside the charge distribution as
\[ \vec{E}_{out} = \left[ \dfrac{aR^{n+3}}{\epsilon_0(n + 3)} \right] \dfrac{1}{r^2} \hat{r}, \nonumber\]
where \(\hat{r}\) is a unit vector in the direction from the origin to the field point at the Gaussian surface.
(b) Field at a point inside the charge distribution. The Gaussian surface is now buried inside the charge distribution, with \(r < R\). Therefore, only those charges in the distribution that are within a distance r of the center of the spherical charge distribution count in \(r_{enc}\):
\[q_{enc} = \int_0^r ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} r^{n+3}. \nonumber\]
Now, using the general result above for \(\vec{E}_{in}\), we find the electric field at a point that is a distance r from the center and lies within the charge distribution as
\[\vec{E}_{in} = \left[ \dfrac{a}{\epsilon_0 ( n + 3)} \right] r^{n+1} \hat{r}, \nonumber\]
where the direction information is included by using the unit radial vector.
Check that the electric fields for the sphere reduce to the correct values for a point charge.
Solution
In this case, there is only \(\vec{E}_{out}\). So, yes.
Charge Distribution with Cylindrical Symmetry
A charge distribution has cylindrical symmetry if the charge density depends only upon the distance r from the axis of a cylinder and must not vary along the axis or with direction about the axis. In other words, if your system varies if you rotate it around the axis, or shift it along the axis, you do not have cylindrical symmetry.
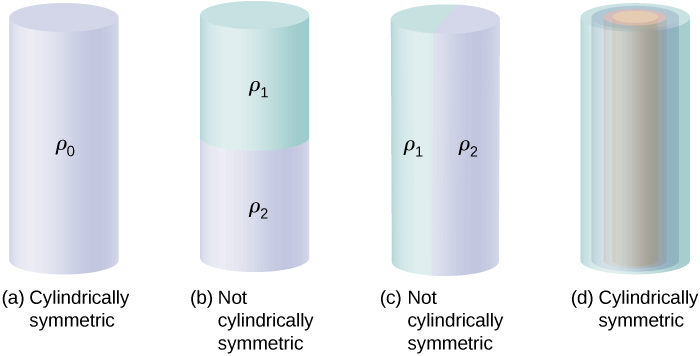
Figure \(\PageIndex{7}\) shows four situations in which charges are distributed in a cylinder. A uniform charge density \(\rho_0\) in an infinite straight wire has a cylindrical symmetry, and so does an infinitely long cylinder with constant charge density \(\rho_0\). An infinitely long cylinder that has different charge densities along its length, such as a charge density \(\rho_1\) for \(z > 0\) and \(\rho_2 \neq \rho_1\) for \(z < 0\), does not have a usable cylindrical symmetry for this course. Neither does a cylinder in which charge density varies with the direction, such as a charge density \(\rho_1\) for \(0 \leq \theta < \pi\) and \(\rho_2 \neq \rho_1\) for \(\pi \leq \theta < 2\pi\). A system with concentric cylindrical shells, each with uniform charge densities, albeit different in different shells, as in FiFigure \(\PageIndex{7d}\), does have cylindrical symmetry if they are infinitely long. The infinite length requirement is due to the charge density changing along the axis of a finite cylinder. In real systems, we don’t have infinite cylinders; however, if the cylindrical object is considerably longer than the radius from it that we are interested in, then the approximation of an infinite cylinder becomes useful.
Consequences of SAymmetry
In all cylindrically symmetrical cases, the electric field \(E_p\) at any point \(P\) must also display cylindrical symmetry.
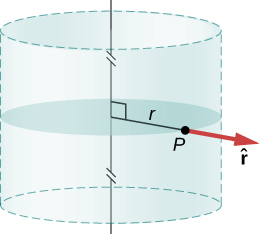
Cylindrical symmetry: \(\vec{E}_p = E_p(r)\hat{r}\), where \(r\) is the distance from the axis and \(\hat{r}\) is a unit vector directed perpendicularly away from the axis (Figure \(\PageIndex{8}\)).
Gaussian surface and flux calculation
To make use of the direction and functional dependence of the electric field, we choose a closed Gaussian surface in the shape of a cylinder with the same axis as the axis of the charge distribution. The flux through this surface of radius s and height L is easy to compute if we divide our task into two parts: (a) a flux through the flat ends and (b) a flux through the curved surface (Figure \(\PageIndex{9}\)).
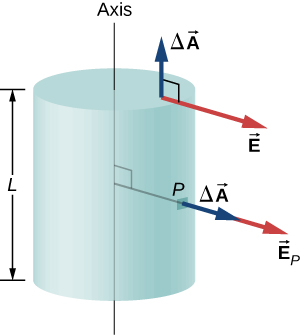
The electric field is perpendicular to the cylindrical side and parallel to the planar end caps of the surface. The flux through the cylindrical part is
\[\int_S \vec{E} \cdot \hat{n} dA = E \int_S dA = E(2\pi r L), \nonumber\]
whereas the flux through the end caps is zero because \(\vec{E} \cdot \hat{n} = 0\) there. Thus, the flux is
\[\int_S \vec{E} \cdot \hat{n} dA = E(2\pi rL) + 0 + 0 = 2\pi rLE. \nonumber\]
Using Gauss’s law
According to Gauss’s law, the flux must equal the amount of charge within the volume enclosed by this surface, divided by the permittivity of free space. When you do the calculation for a cylinder of length L, you find that \(q_{enc}\) of Gauss’s law is directly proportional to L. Let us write it as charge per unit length (\(\lambda_{enc}\)) times length L:
\[q_{enc} = \lambda_{enc} L.\]
Hence, Gauss’s law for any cylindrically symmetrical charge distribution yields the following magnitude of the electric field a distance s away from the axis:
\[Magnitude: \, E(r) = \dfrac{\lambda_{enc}}{2\pi \epsilon_0} \dfrac{1}{r}.\]
The charge per unit length \(\lambda_{enc}\) depends on whether the field point is inside or outside the cylinder of charge distribution, just as we have seen for the spherical distribution.
Computing enclosed charge
Let R be the radius of the cylinder within which charges are distributed in a cylindrically symmetrical way. Let the field point P be at a distance s from the axis. (The side of the Gaussian surface includes the field point P.) When \(r > R\) (that is, when P is outside the charge distribution), the Gaussian surface includes all the charge in the cylinder of radius R and length L. When \(r < R\) (P is located inside the charge distribution), then only the charge within a cylinder of radius s and length L is enclosed by the Gaussian surface:
\(\lambda_{enc} = (total \, charge) \, if \, r \geq R\)
\(\lambda_{enc} = (only \, charge \, within \, t < R) \, if \, r < R\)
A very long non-conducting cylindrical shell of radius R has a uniform surface charge density \(\sigma_0\) Find the electric field (a) at a point outside the shell and (b) at a point inside the shell.
Strategy
Apply the Gauss’s law strategy given earlier, where we treat the cases inside and outside the shell separately.
Solution
a.Electric field at a point outside the shell. For a point outside the cylindrical shell, the Gaussian surface is the surface of a cylinder of radius \(r > R\) and length L, as shown in Figure \(\PageIndex{10}\). The charge enclosed by the Gaussian cylinder is equal to the charge on the cylindrical shell of length L. Therefore, \(\lambda_{enc}\) is given by \[\lambda_{enc} = \dfrac{\sigma_0 2\pi RL}{L} = 2\pi R \sigma_0.\]
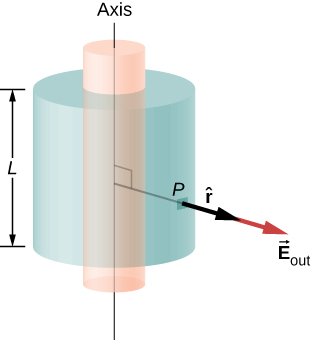
Hence, the electric field at a point P outside the shell at a distance r away from the axis is
\[\vec{E} = \dfrac{2\pi R \sigma_0}{2 \pi \epsilon_0} \dfrac{1}{r} \hat{r} = \dfrac{R\sigma_0}{\epsilon_0} \dfrac{1}{r} \hat{r} \, (r > R)\]
where \(\hat{r}\) is a unit vector, perpendicular to the axis and pointing away from it, as shown in the figure. The electric field at P points in the direction of \(\hat{r}\) given in Figure \(\PageIndex{10}\) if \(\sigma_0 > 0\) and in the opposite direction to \(\hat{r}\) if \(\sigma_0 <0\).
b. Electric field at a point inside the shell. For a point inside the cylindrical shell, the Gaussian surface is a cylinder whose radius r is less than R (Figure \(\PageIndex{11}\)). This means no charges are included inside the Gaussian surface:
\[\lambda_{enc} = 0.\]
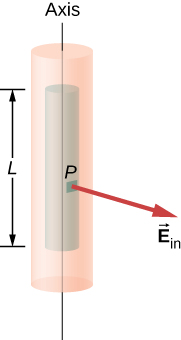
This gives the following equation for the magnitude of the electric field \(E_{in}\) at a point whose r is less than R of the shell of charges.
\[E_{in} 2\pi rL = 0 (r<R), \nonumber\]
This gives us
\[E_{in} = 0 (r < R). \nonumber\]
Significance
Notice that the result inside the shell is exactly what we should expect: No enclosed charge means zero electric field. Outside the shell, the result becomes identical to a wire with uniform charge \(R\sigma\).
A thin straight wire has a uniform linear charge density \(\lambda_0\). Find the electric field at a distance d from the wire, where d is much less than the length of the wire.
Solution
\(\vec{E} = \frac{\lambda_0}{2\pi \epsilon_0} \frac{1}{d} \hat{r}\); This agrees with the calculation of [link] where we found the electric field by integrating over the charged wire. Notice how much simpler the calculation of this electric field is with Gauss’s law.
Charge Distribution with Planar Symmetry
A planar symmetry of charge density is obtained when charges are uniformly spread over a large flat surface. In planar symmetry, all points in a plane parallel to the plane of charge are identical with respect to the charges.
Consequences of symmetry
We take the plane of the charge distribution to be the xy-plane and we find the electric field at a space point P with coordinates (x, y, z). Since the charge density is the same at all (x, y)-coordinates in the \(z = 0\) plane, by symmetry, the electric field at P cannot depend on the x- or y-coordinates of point P, as shown in Figure \(\PageIndex{12}\). Therefore, the electric field at P can only depend on the distance from the plane and has a direction either toward the plane or away from the plane. That is, the electric field at P has only a nonzero z-component.
Uniform charges in xy plane: \(\vec{E} = E(z) \hat{z}\) where z is the distance from the plane and \(\hat{z}\) is the unit vector normal to the plane. Note that in this system, \(E(z) = E(-z)\), although of course they point in opposite directions.
Gaussian surface and flux calculation
In the present case, a convenient Gaussian surface is a box, since the expected electric field points in one direction only. To keep the Gaussian box symmetrical about the plane of charges, we take it to straddle the plane of the charges, such that one face containing the field point P is taken parallel to the plane of the charges. In Figure \(\PageIndex{13}\), sides I and II of the Gaussian surface (the box) that are parallel to the infinite plane have been shaded. They are the only surfaces that give rise to nonzero flux because the electric field and the area vectors of the other faces are perpendicular to each other.
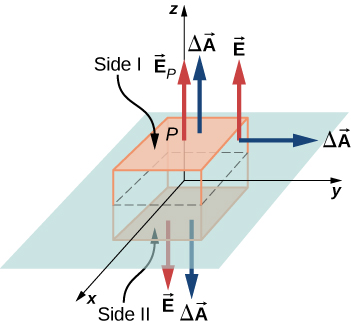
Let A be the area of the shaded surface on each side of the plane and EP
be the magnitude of the electric field at point P. Since sides I and II are at the same distance from the plane, the electric field has the same magnitude at points in these planes, although the directions of the electric field at these points in the two planes are opposite to each other.
Magnitude at I or II: \(E(z) = E_p\).
If the charge on the plane is positive, then the direction of the electric field and the area vectors are as shown in Figure \(\PageIndex{13}\). Therefore, we find for the flux of electric field through the box
\[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\]
where the zeros are for the flux through the other sides of the box. Note that if the charge on the plane is negative, the directions of electric field and area vectors for planes I and II are opposite to each other, and we get a negative sign for the flux. According to Gauss’s law, the flux must equal \(q_{enc}/\epsilon_0\). From Figure \(\PageIndex{13}\), we see that the charges inside the volume enclosed by the Gaussian box reside on an area A of the xy-plane. Hence,
\[q_{enc} = \sigma_0 A. \nonumber\]
Using the equations for the flux and enclosed charge in Gauss’s law, we can immediately determine the electric field at a point at height z from a uniformly charged plane in the xy-plane:
\[\vec{E}_p = \dfrac{\sigma_0}{2\epsilon_0} \hat{n}. \nonumber\]
The direction of the field depends on the sign of the charge on the plane and the side of the plane where the field point P is located. Note that above the plane, \(\hat{n} = + \hat{z}\), while below the plane, \(\hat{n} = - \hat{z}\).
You may be surprised to note that the electric field does not actually depend on the distance from the plane; this is an effect of the assumption that the plane is infinite. In practical terms, the result given above is still a useful approximation for finite planes near the center.


