7.4: Calculations of Electric Potential
- Page ID
- 4388
By the end of this section, you will be able to:
- Calculate the potential due to a point charge
- Calculate the potential of a system of multiple point charges
- Describe an electric dipole
- Define dipole moment
- Calculate the potential of a continuous charge distribution
Point charges, such as electrons, are among the fundamental building blocks of matter. Furthermore, spherical charge distributions (such as charge on a metal sphere) create external electric fields exactly like a point charge. The electric potential due to a point charge is, thus, a case we need to consider.
We can use calculus to find the work needed to move a test charge q from a large distance away to a distance of r from a point charge q. Noting the connection between work and potential \(W = -q\Delta V\), as in the last section, we can obtain the following result.
The electric potential \(V\) of a point charge is given by
\[\underbrace{V = \dfrac{kq}{r}}_{\text{point charge}} \label{PointCharge}\]
where \(k\) is a constant equal to \(9.0 \times 10^9 \, N \cdot m^2/C^2\).
The potential in Equation \ref{PointCharge} at infinity is chosen to be zero. Thus, \(V\) for a point charge decreases with distance, whereas \(\vec{E}\) for a point charge decreases with distance squared:
\[E = \dfrac{F}{q_t} = \dfrac{kq}{r^2}\]
Recall that the electric potential V is a scalar and has no direction, whereas the electric field \(\vec{E}\) is a vector. To find the voltage due to a combination of point charges, you add the individual voltages as numbers. To find the total electric field, you must add the individual fields as vectors, taking magnitude and direction into account. This is consistent with the fact that V is closely associated with energy, a scalar, whereas \(\vec{E}\) is closely associated with force, a vector.
Charges in static electricity are typically in the nanocoulomb (nC) to microcoulomb \((\mu C)\) range. What is the voltage 5.00 cm away from the center of a 1-cm-diameter solid metal sphere that has a –3.00-nC static charge?
Strategy
As we discussed in Electric Charges and Fields, charge on a metal sphere spreads out uniformly and produces a field like that of a point charge located at its center. Thus, we can find the voltage using the equation \(V = \dfrac{kq}{r}\).
Solution
Entering known values into the expression for the potential of a point charge (Equation \ref{PointCharge}), we obtain
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (9.00 \times 10^9 \, N \cdot m^2/C^2)\left(\dfrac{-3.00 \times 10^{-9}C}{5.00 \times 10^{-2}m}\right) \nonumber \\[4pt] &= - 539 \, V. \nonumber \end{align} \nonumber \]
Significance
The negative value for voltage means a positive charge would be attracted from a larger distance, since the potential is lower (more negative) than at larger distances. Conversely, a negative charge would be repelled, as expected.
A demonstration Van de Graaff generator has a 25.0-cm-diameter metal sphere that produces a voltage of 100 kV near its surface (Figure). What excess charge resides on the sphere? (Assume that each numerical value here is shown with three significant figures.)
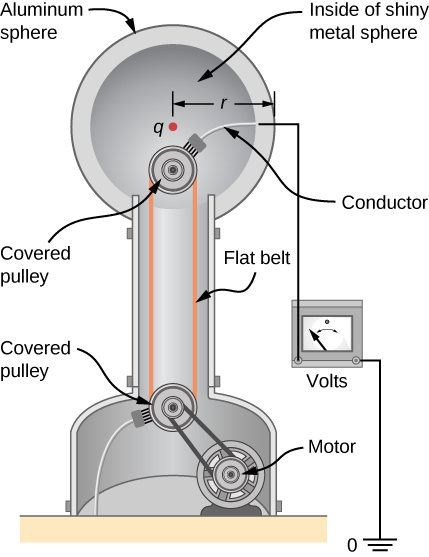
Strategy
The potential on the surface is the same as that of a point charge at the center of the sphere, 12.5 cm away. (The radius of the sphere is 12.5 cm.) We can thus determine the excess charge using Equation \ref{PointCharge}
\[V = \dfrac{kq}{r}.\]
Solution
Solving for \(q\) and entering known values gives
\[\begin{align} q &= \dfrac{rV}{k} \nonumber \\[4pt] &= \dfrac{(0.125 \, m)(100 \times 10^3 \, V)}{8.99 \times 10^9 N \cdot m^2/C^2} \nonumber \\[4pt] &= 1.39 \times 10^{-6} C \nonumber \\[4pt] &= 1.39 \, \mu C. \nonumber \end{align} \nonumber \]
Significance
This is a relatively small charge, but it produces a rather large voltage. We have another indication here that it is difficult to store isolated charges.
What is the potential inside the metal sphere in Example \(\PageIndex{1}\)?
Solution
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (8.99 \times 10^9 N \cdot m^2/C^2) \left(\dfrac{-3.00 \times 10^{-9} C}{5.00 \times 10^{-3} m}\right) \nonumber \\[4pt] &= - 5390 \, V\nonumber \end{align} \nonumber \]
Recall that the electric field inside a conductor is zero. Hence, any path from a point on the surface to any point in the interior will have an integrand of zero when calculating the change in potential, and thus the potential in the interior of the sphere is identical to that on the surface.
The voltages in both of these examples could be measured with a meter that compares the measured potential with ground potential. Ground potential is often taken to be zero (instead of taking the potential at infinity to be zero). It is the potential difference between two points that is of importance, and very often there is a tacit assumption that some reference point, such as Earth or a very distant point, is at zero potential. As noted earlier, this is analogous to taking sea level as \(h = 0\) when considering gravitational potential energy \(U_g = mgh\).
Systems of Multiple Point Charges
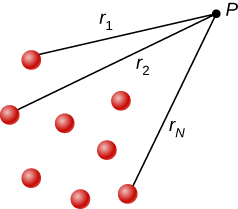
Just as the electric field obeys a superposition principle, so does the electric potential. Consider a system consisting of N charges \(q_1,q_2,. . ., q_N\). What is the net electric potential V at a space point P from these charges? Each of these charges is a source charge that produces its own electric potential at point P, independent of whatever other changes may be doing. Let \(V_1, V_2, . . ., V_N\) be the electric potentials at P produced by the charges \(q_1,q_2,. . ., q_N\), respectively. Then, the net electric potential \(V_p\) at that point is equal to the sum of these individual electric potentials. You can easily show this by calculating the potential energy of a test charge when you bring the test charge from the reference point at infinity to point P:
\[V_p = V_1 + V_2 + . . . + V_N = \sum_1^N V_i.\]
Note that electric potential follows the same principle of superposition as electric field and electric potential energy. To show this more explicitly, note that a test charge \(q_i\) at the point P in space has distances of \(r_1,r_2, . . . ,r_N\) from the N charges fixed in space above, as shown in Figure \(\PageIndex{2}\). Using our formula for the potential of a point charge for each of these (assumed to be point) charges, we find that
\[V_p = \sum_1^N k\dfrac{q_i}{r_i} = k\sum_1^N \dfrac{q_i}{r_i}. \label{eq20}\]
Therefore, the electric potential energy of the test charge is
\[U_p = q_tV_p = q_tk\sum_1^N \dfrac{q_i}{r_i},\] which is the same as the work to bring the test charge into the system, as found in the first section of the chapter.
The Electric Dipole
An electric dipole is a system of two equal but opposite charges a fixed distance apart. This system is used to model many real-world systems, including atomic and molecular interactions. One of these systems is the water molecule, under certain circumstances. These circumstances are met inside a microwave oven, where electric fields with alternating directions make the water molecules change orientation. This vibration is the same as heat at the molecular level.
Consider the dipole in Figure \(\PageIndex{3}\) with the charge magnitude of \(q = 3.0 \, \mu C\) and separation distance \(d = 4.0 \, cm.\) What is the potential at the following locations in space? (a) (0, 0, 1.0 cm); (b) (0, 0, –5.0 cm); (c) (3.0 cm, 0, 2.0 cm).
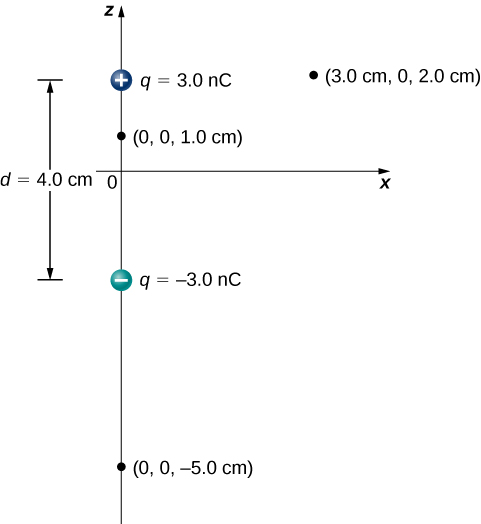
Strategy
Apply \(V_p = k \sum_1^N \dfrac{q_i}{r_i}\) to each of these three points.
Solution
a. \(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.010 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = 1.8 \times 10^3 \, V\)
b. \(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.070 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = -5.1 \times 10^2 \, V\)
c. \(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.030 \, m} - \dfrac{3.0\space nC}{0.050 \, m}\right) = 3.6 \times 10^2 \, V\)
Significance
Note that evaluating potential is significantly simpler than electric field, due to potential being a scalar instead of a vector.
What is the potential on the x-axis? The z-axis
Solution
The x-axis the potential is zero, due to the equal and opposite charges the same distance from it. On the z-axis, we may superimpose the two potentials; we will find that for \(z > > d\), again the potential goes to zero due to cancellation.
Now let us consider the special case when the distance of the point P from the dipole is much greater than the distance between the charges in the dipole, \(r >> d\); for example, when we are interested in the electric potential due to a polarized molecule such as a water molecule. This is not so far (infinity) that we can simply treat the potential as zero, but the distance is great enough that we can simplify our calculations relative to the previous example.
We start by noting that in Figure \(\PageIndex{4}\) the potential is given by
\[V_p = V_+ + V_- = k \left( \dfrac{q}{r_+} - \dfrac{q}{r_-} \right)\]
where
\[r_{\pm} = \sqrt{x^2 + \left(z \pm \dfrac{d}{2}\right)^2}.\]
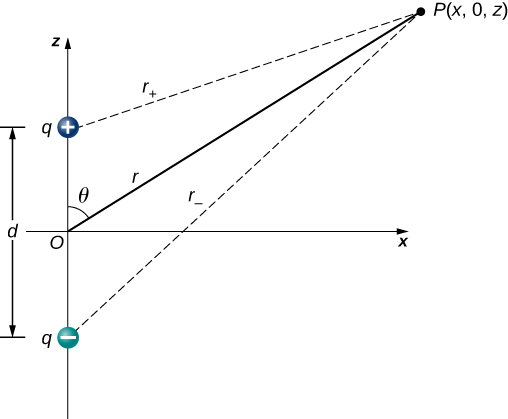
This is still the exact formula. To take advantage of the fact that \(r \gg d\), we rewrite the radii in terms of polar coordinates, with \(x = r \, \sin \, \theta\) and z = r \, \cos \, \theta\). This gives us
\[r_{\pm} = \sqrt{r^2 \, \sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}.\]
We can simplify this expression by pulling r out of the root,
\[r_{\pm} = \sqrt{\sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}\]
and then multiplying out the parentheses
\[r_{\pm} = r \sqrt{\sin^2\space \theta + \cos^2 \, \theta \pm \cos \, \theta\dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2}.\]
The last term in the root is small enough to be negligible (remember \(r >> d\), and hence \((d/r)^2\) is extremely small, effectively zero to the level we will probably be measuring), leaving us with
\[r_{\pm} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r}}.\]
Using the binomial approximation (a standard result from the mathematics of series, when \(a\) is small)
\[\dfrac{1}{\sqrt{1 \pm a}} \approx 1 \pm \dfrac{a}{2}\]
and substituting this into our formula for \(V_p\), we get
\[V_p = k\left[\dfrac{q}{r}\left(1 + \dfrac{d \, \cos \, \theta}{2r} \right) - \dfrac{q}{r}\left(1 - \dfrac{d \, \cos \, \theta}{2r}\right)\right] = k\dfrac{qd \, \cos \theta}{r^2}.\]
This may be written more conveniently if we define a new quantity, the electric dipole moment,
\[\vec{p} = q\vec{d},\]
where these vectors point from the negative to the positive charge. Note that this has magnitude qd. This quantity allows us to write the potential at point P due to a dipole at the origin as
\[V_p = k\dfrac{\vec{p} \cdot \hat{r}}{r^2}.\]
A diagram of the application of this formula is shown in Figure \(\PageIndex{5}\).
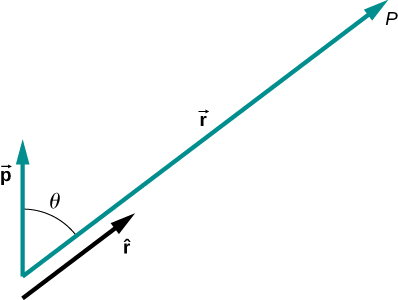
There are also higher-order moments, for quadrupoles, octupoles, and so on. You will see these in future classes.
Potential of Continuous Charge Distributions
We have been working with point charges a great deal, but what about continuous charge distributions? Recall from Equation \ref{eq20} that
\[V_p = k\sum \dfrac{q_i}{r_i}.\]
We may treat a continuous charge distribution as a collection of infinitesimally separated individual points. This yields the integral
\[V_p = \int \dfrac{dq}{r}\]
for the potential at a point P. Note that \(r\) is the distance from each individual point in the charge distribution to the point P. As we saw in Electric Charges and Fields, the infinitesimal charges are given by
\[\underbrace{dq = \lambda \, dl}_{one \, dimension}\]
\[\underbrace{dq = \sigma \, dA}_{two \, dimensions}\]
\[\underbrace{dq = \rho \, dV \space}_{three \, dimensions}\]
where \(\lambda\) is linear charge density, \(\sigma\) is the charge per unit area, and \(\rho\) is the charge per unit volume.
Find the electric potential of a uniformly charged, nonconducting wire with linear density \(\lambda\) (coulomb/meter) and length L at a point that lies on a line that divides the wire into two equal parts.
Strategy
To set up the problem, we choose Cartesian coordinates in such a way as to exploit the symmetry in the problem as much as possible. We place the origin at the center of the wire and orient the y-axis along the wire so that the ends of the wire are at \(y = \pm L/2\). The field point P is in the xy-plane and since the choice of axes is up to us, we choose the x-axis to pass through the field point P, as shown in Figure \(\PageIndex{6}\).
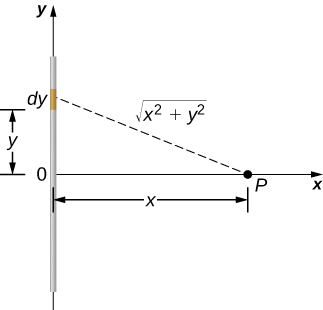
Solution
Consider a small element of the charge distribution between y and \(y + dy\). The charge in this cell is \(dq = \lambda \, dy\) and the distance from the cell to the field point P is \(\sqrt{x^2 + y^2}\). Therefore, the potential becomes
\[\begin{align} V_p &= k \int \dfrac{dq}{r} \nonumber \\[4pt] &= k\int_{-L/2}^{L/2} \dfrac{\lambda \, dy}{\sqrt{x^2 + y^2}} \nonumber \\[4pt] &= k\lambda \left[ln \left(y + \sqrt{y^2 + x^2}\right) \right]_{-L/2}^{L/2} \nonumber \\[4pt] &= k\lambda \left[ ln \left(\left(\dfrac{L}{2}\right) + \sqrt{\left(\dfrac{L}{2}\right)^2 + x^2}\right) - ln\left(\left(-\dfrac{L}{2}\right) + \sqrt{\left(-\dfrac{L}{2}\right)^2 + x^2}\right)\right] \nonumber \\[4pt] &= k\lambda ln \left[ \dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right]. \nonumber \end{align} \nonumber\]
Significance
Note that this was simpler than the equivalent problem for electric field, due to the use of scalar quantities. Recall that we expect the zero level of the potential to be at infinity, when we have a finite charge. To examine this, we take the limit of the above potential as x approaches infinity; in this case, the terms inside the natural log approach one, and hence the potential approaches zero in this limit. Note that we could have done this problem equivalently in cylindrical coordinates; the only effect would be to substitute r for x and z for y.
A ring has a uniform charge density \(\lambda\), with units of coulomb per unit meter of arc. Find the electric potential at a point on the axis passing through the center of the ring.
Strategy
We use the same procedure as for the charged wire. The difference here is that the charge is distributed on a circle. We divide the circle into infinitesimal elements shaped as arcs on the circle and use cylindrical coordinates shown in Figure \(\PageIndex{7}\).
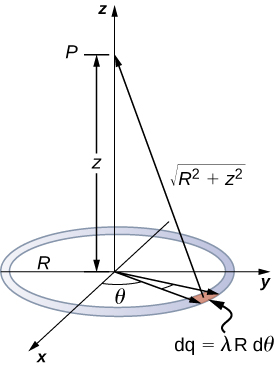
Solution
A general element of the arc between \(\theta\) and \(\theta + d\theta\) is of length \(Rd\theta\) and therefore contains a charge equal to \(\lambda Rd\theta\). The element is at a distance of \(\sqrt{z^2 + R^2}\) from P, and therefore the potential is
\[\begin{align} V_p &= k\int \dfrac{dq}{r} \nonumber \\[4pt] &= k \int_0^{2\pi} \dfrac{\lambda Rd\theta}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= \dfrac{k \lambda R}{\sqrt{z^2 + R^2}} \int_0^{2\pi} d\theta \nonumber \\[4pt] &= \dfrac{2\pi k \lambda R}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}}. \nonumber \end{align} \nonumber\]
Significance
This result is expected because every element of the ring is at the same distance from point P. The net potential at P is that of the total charge placed at the common distance, \(\sqrt{z^2 + R^2}\).
A disk of radius R has a uniform charge density \(\sigma\) with units of coulomb meter squared. Find the electric potential at any point on the axis passing through the center of the disk.
Strategy
We divide the disk into ring-shaped cells, and make use of the result for a ring worked out in the previous example, then integrate over r in addition to \(\theta\). This is shown in Figure \(\PageIndex{8}\).
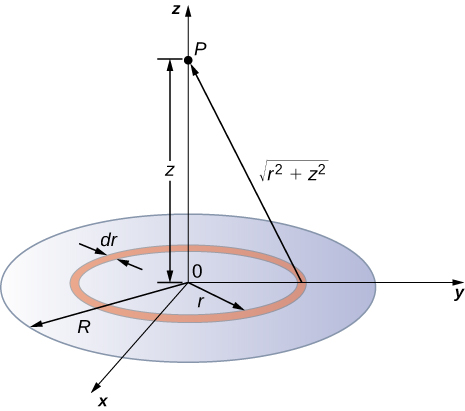
Solution
An infinitesimal width cell between cylindrical coordinates r and \(r + dr\) shown in Figure \(\PageIndex{8}\) will be a ring of charges whose electric potential \(dV_p\) at the field point has the following expression
\[dV_p = k \dfrac{dq}{\sqrt{z^2 + r^2}}\]
where
\[dq = \sigma 2\pi r dr.\]
The superposition of potential of all the infinitesimal rings that make up the disk gives the net potential at point P. This is accomplished by integrating from \(r = 0\) to \(r = R\):
\[\begin{align} V_p &= \int dV_p = k2\pi \sigma \int_0^R \dfrac{r \, dr}{\sqrt{z^2 + r^2}}, \nonumber \\[4pt] &= k2\pi \sigma ( \sqrt{z^2 + R^2} - \sqrt{z^2}).\nonumber \end{align} \nonumber\]
Significance
The basic procedure for a disk is to first integrate around θ and then over r. This has been demonstrated for uniform (constant) charge density. Often, the charge density will vary with r, and then the last integral will give different results.
Find the electric potential due to an infinitely long uniformly charged wire.
Strategy
Since we have already worked out the potential of a finite wire of length L in Example \(\PageIndex{4}\), we might wonder if taking \(L \rightarrow \infty\) in our previous result will work:
\[V_p = \lim_{L \rightarrow \infty} k \lambda \ln \left(\dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right).\]
However, this limit does not exist because the argument of the logarithm becomes [2/0] as \(L \rightarrow \infty\), so this way of finding V of an infinite wire does not work. The reason for this problem may be traced to the fact that the charges are not localized in some space but continue to infinity in the direction of the wire. Hence, our (unspoken) assumption that zero potential must be an infinite distance from the wire is no longer valid.
To avoid this difficulty in calculating limits, let us use the definition of potential by integrating over the electric field from the previous section, and the value of the electric field from this charge configuration from the previous chapter.
Solution
We use the integral
\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]
where R is a finite distance from the line of charge, as shown in Figure \(\PageIndex{9}\).
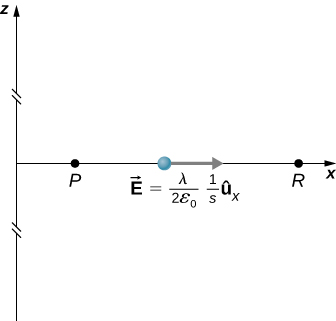
With this setup, we use \(\vec{E}_p = 2k \lambda \dfrac{1}{s} \hat{s}\) and \(d\vec{l} = d\vec{s}\) to obtain
\[\begin{align} V_p - V_R &= - \int_R^p 2k\lambda \dfrac{1}{s}ds \nonumber \\[4pt] &= -2 k \lambda \ln\dfrac{s_p}{s_R}. \nonumber \end{align} \nonumber\]
Now, if we define the reference potential \(V_R = 0\) at \(s_R = 1 \, m\), this simplifies to
\[V_p = -2 k\lambda \, \ln \, s_p.\]
Note that this form of the potential is quite usable; it is 0 at 1 m and is undefined at infinity, which is why we could not use the latter as a reference.
Significance
Although calculating potential directly can be quite convenient, we just found a system for which this strategy does not work well. In such cases, going back to the definition of potential in terms of the electric field may offer a way forward.
What is the potential on the axis of a nonuniform ring of charge, where the charge density is \(\lambda (\theta) = \lambda \, \cos \, \theta\)?
Solution
It will be zero, as at all points on the axis, there are equal and opposite charges equidistant from the point of interest. Note that this distribution will, in fact, have a dipole moment.


