12.5: Stress, Strain, and Elastic Modulus (Part 2)
- Page ID
- 6472
Bulk Stress, Strain, and Modulus
When you dive into water, you feel a force pressing on every part of your body from all directions. What you are experiencing then is bulk stress, or in other words, pressure. Bulk stress always tends to decrease the volume enclosed by the surface of a submerged object. The forces of this “squeezing” are always perpendicular to the submerged surface Figure \(\PageIndex{1}\). The effect of these forces is to decrease the volume of the submerged object by an amount \(\Delta\)V compared with the volume V0 of the object in the absence of bulk stress. This kind of deformation is called bulk strain and is described by a change in volume relative to the original volume:
\[bulk\; strain = \frac{\Delta V}{V_{0}} \label{12.37}\]
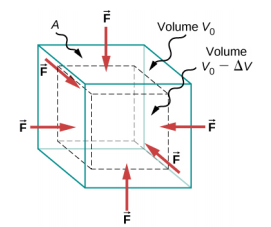
The bulk strain results from the bulk stress, which is a force F\(\perp\) normal to a surface that presses on the unit surface area A of a submerged object. This kind of physical quantity, or pressure p, is defined as
\[pressure = p \equiv \frac{F_{\perp}}{A} \ldotp \label{12.38}\]
We will study pressure in fluids in greater detail in Fluid Mechanics. An important characteristic of pressure is that it is a scalar quantity and does not have any particular direction; that is, pressure acts equally in all possible directions. When you submerge your hand in water, you sense the same amount of pressure acting on the top surface of your hand as on the bottom surface, or on the side surface, or on the surface of the skin between your fingers. What you are perceiving in this case is an increase in pressure \(\Delta\)p over what you are used to feeling when your hand is not submerged in water. What you feel when your hand is not submerged in the water is the normal pressure p0 of one atmosphere, which serves as a reference point. The bulk stress is this increase in pressure, or \(\Delta\)p, over the normal level, p0.
When the bulk stress increases, the bulk strain increases in response, in accordance with Equation 12.4.4. The proportionality constant in this relation is called the bulk modulus, B, or
\[B = \frac{bulk\; stress}{bulk\; strain} = \frac{\Delta p}{\frac{\Delta V}{V_{0}}} = - \Delta p \frac{V_{0}}{\Delta V} \ldotp \label{12.39}\]
The minus sign that appears in Equation \ref{12.39} is for consistency, to ensure that \(B\) is a positive quantity. Note that the minus sign (–) is necessary because an increase \(\Delta\)p in pressure (a positive quantity) always causes a decrease \(\Delta\)V in volume, and decrease in volume is a negative quantity. The reciprocal of the bulk modulus is called compressibility k, or
\[k = \frac{1}{B} = - \frac{\frac{\Delta V}{V_{0}}}{\Delta p} \ldotp \label{12.40}\]
The term ‘compressibility’ is used in relation to fluids (gases and liquids). Compressibility describes the change in the volume of a fluid per unit increase in pressure. Fluids characterized by a large compressibility are relatively easy to compress. For example, the compressibility of water is 4.64 x 10−5 /atm and the compressibility of acetone is 1.45 x 10−4 /atm. This means that under a 1.0-atm increase in pressure, the relative decrease in volume is approximately three times as large for acetone as it is for water.
In a hydraulic press Figure \(\PageIndex{2}\), a 250-liter volume of oil is subjected to a 2300-psi pressure increase. If the compressibility of oil is 2.0 x 10−5 / atm, find the bulk strain and the absolute decrease in the volume of oil when the press is operating.
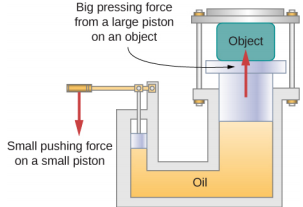
Strategy
We must invert Equation \ref{12.40} to find the bulk strain. First, we convert the pressure increase from psi to atm, \(\Delta\)p = 2300 psi = \(\frac{2300}{14.7\; atm}\) ≈ 160 atm, and identify V0 = 250 L.
Solution
Substituting values into the equation, we have
\[bulk\; strain = \frac{\Delta V}{V_{0}} = \frac{\Delta p}{B} = k \Delta p = (2.0 \times 10^{-5}\; /atm)(160\; atm) = 0.0032\]
answer
\[\Delta V = 0.0032 V_{0} = 0.0032 (250\; L) = 0.78\; L \ldotp\]
Significance
Notice that since the compressibility of water is 2.32 times larger than that of oil, if the working substance in the hydraulic press of this problem were changed to water, the bulk strain as well as the volume change would be 2.32 times larger.
If the normal force acting on each face of a cubical 1.0-m3 piece of steel is changed by 1.0 x 107 N, find the resulting change in the volume of the piece of steel.
Shear Stress, Strain, and Modulus
The concepts of shear stress and strain concern only solid objects or materials. Buildings and tectonic plates are examples of objects that may be subjected to shear stresses. In general, these concepts do not apply to fluids.
Shear deformation occurs when two antiparallel forces of equal magnitude are applied tangentially to opposite surfaces of a solid object, causing no deformation in the transverse direction to the line of force, as in the typical example of shear stress illustrated in Figure \(\PageIndex{3}\). Shear deformation is characterized by a gradual shift \(\Delta\)x of layers in the direction tangent to the acting forces. This gradation in \(\Delta\)x occurs in the transverse direction along some distance L0. Shear strain is defined by the ratio of the largest displacement \(\Delta\)x to the transverse distance L0
\[shear\; strain = \frac{\Delta x}{L_{0}} \ldotp \label{12.41}\]
Shear strain is caused by shear stress. Shear stress is due to forces that act parallel to the surface. We use the symbol F\(\parallel\) for such forces. The magnitude F\(\parallel\) per surface area A where shearing force is applied is the measure of shear stress
\[shear\; stress = \frac{F_{\parallel}}{A} \ldotp \label{12.42}\]
The shear modulus is the proportionality constant in Equation \ref{12.33} and is defined by the ratio of stress to strain. Shear modulus is commonly denoted by \(S\):
\[S = \frac{shear\; stress}{shear\; strain} = \frac{\frac{F_{\parallel}}{A}}{\frac{\Delta x}{L_{0}}} = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} \ldotp \label{12.43}\]
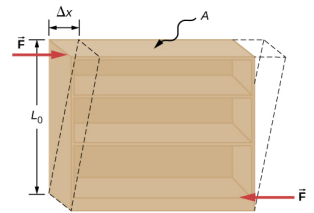
A cleaning person tries to move a heavy, old bookcase on a carpeted floor by pushing tangentially on the surface of the very top shelf. However, the only noticeable effect of this effort is similar to that seen in Figure \(\PageIndex{2}\), and it disappears when the person stops pushing. The bookcase is 180.0 cm tall and 90.0 cm wide with four 30.0-cm-deep shelves, all partially loaded with books. The total weight of the bookcase and books is 600.0 N. If the person gives the top shelf a 50.0-N push that displaces the top shelf horizontally by 15.0 cm relative to the motionless bottom shelf, find the shear modulus of the bookcase.
Strategy
The only pieces of relevant information are the physical dimensions of the bookcase, the value of the tangential force, and the displacement this force causes. We identify F\(\parallel\) = 50.0 N, \(\Delta\)x = 15.0 cm, L0 = 180.0 cm, and A = (30.0 cm)(90.0 cm) = 2700.0 cm2, and we use Equation \ref{12.43} to compute the shear modulus.
Solution
Substituting numbers into the equations, we obtain for the shear modulus
\[S = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} = \frac{50.0\; N}{2700.0\; cm^{2}} \frac{180.0\; cm}{15.0\; cm} = \frac{2}{9} \frac{M}{cm^{2}} = \frac{2}{9} \times 10^{4}\; N/m^{2} = \frac{20}{9} \times 10^{3}\; Pa = 2.222\; kPa \ldotp \nonumber\]
We can also find shear stress and strain, respectively:
\[\frac{F_{\parallel}}{A} = \frac{50.0\; N}{2700.0\; cm^{2}} = \frac{5}{27}\; kPa = 185.2\; Pa \nonumber\]
\[\frac{\Delta x}{L_{0}} = \frac{15.0\; cm}{180.0\; cm} = \frac{1}{12} = 0.083 \ldotp \nonumber\]
Significance
If the person in this example gave the shelf a healthy push, it might happen that the induced shear would collapse it to a pile of rubbish. Much the same shear mechanism is responsible for failures of earth-filled dams and levees; and, in general, for landslides.
Explain why the concepts of Young’s modulus and shear modulus do not apply to fluids.


