24.E: Electromagnetic Waves (Exercises)
- Last updated
- Save as PDF
- Page ID
- 7819
Conceptual Questions
24.2: Production of Electromagnetic Waves
1. The direction of the electric field shown in each part of Figure 1 is that produced by the charge distribution in the wire. Justify the direction shown in each part, using the Coulomb force law and the definition of \(\displaystyle E = F/q\), where \(\displaystyle q\) is a positive test charge.
2. Is the direction of the magnetic field shown in Figure 2a consistent with the right-hand rule for current (RHR-2) in the direction shown in the figure?
3. Why is the direction of the current shown in each part of Figure 2 opposite to the electric field produced by the wire’s charge separation?
4. In which situation shown in the figure will the electromagnetic wave be more successful in inducing a current in the wire? Explain.
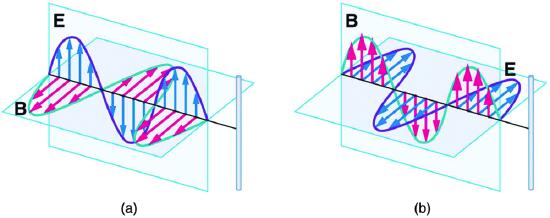
Electromagnetic waves approaching long straight wires.
5. In which situation shown in the figure will the electromagnetic wave be more successful in inducing a current in the loop? Explain.
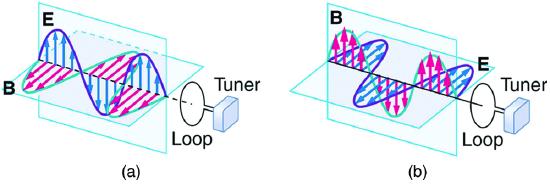
Electromagnetic waves approaching a wire loop.
6. Should the straight wire antenna of a radio be vertical or horizontal to best receive radio waves broadcast by a vertical transmitter antenna? How should a loop antenna be aligned to best receive the signals? (Note that the direction of the loop that produces the best reception can be used to determine the location of the source. It is used for that purpose in tracking tagged animals in nature studies, for example.)
7. Under what conditions might wires in a DC circuit emit electromagnetic waves?
8. Give an example of interference of electromagnetic waves.
9. The figure shows the interference pattern of two radio antennas broadcasting the same signal. Explain how this is analogous to the interference pattern for sound produced by two speakers. Could this be used to make a directional antenna system that broadcasts preferentially in certain directions? Explain.
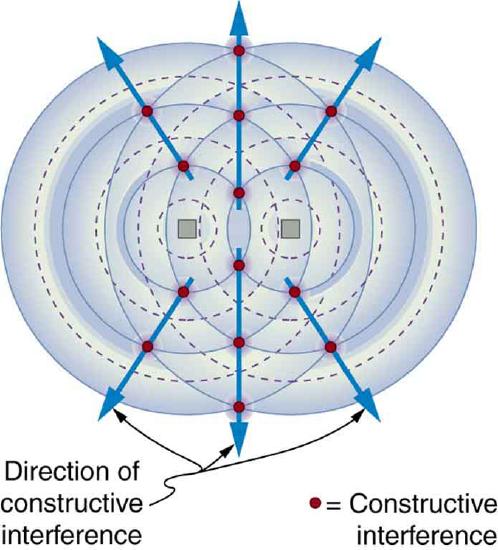
An overhead view of two radio broadcast antennas sending the same signal, and the interference pattern they produce.
10. Can an antenna be any length? Explain your answer.
24.3: The Electromagnetic Spectrum
11. If you live in a region that has a particular TV station, you can sometimes pick up some of its audio portion on your FM radio receiver. Explain how this is possible. Does it imply that TV audio is broadcast as FM?
12. Explain why people who have the lens of their eye removed because of cataracts are able to see low-frequency ultraviolet.
13. How do fluorescent soap residues make clothing look “brighter and whiter” in outdoor light? Would this be effective in candlelight?
14. Give an example of resonance in the reception of electromagnetic waves.
15.Illustrate that the size of details of an object that can be detected with electromagnetic waves is related to their wavelength, by comparing details observable with two different types (for example, radar and visible light or infrared and X-rays).
16. Why don’t buildings block radio waves as completely as they do visible light?
17. Make a list of some everyday objects and decide whether they are transparent or opaque to each of the types of electromagnetic waves.
18. Your friend says that more patterns and colors can be seen on the wings of birds if viewed in ultraviolet light. Would you agree with your friend? Explain your answer.
19. The rate at which information can be transmitted on an electromagnetic wave is proportional to the frequency of the wave. Is this consistent with the fact that laser telephone transmission at visible frequencies carries far more conversations per optical fiber than conventional electronic transmission in a wire? What is the implication for ELF radio communication with submarines?
20. Give an example of energy carried by an electromagnetic wave.
21. In an MRI scan, a higher magnetic field requires higher frequency radio waves to resonate with the nuclear type whose density and location is being imaged. What effect does going to a larger magnetic field have on the most efficient antenna to broadcast those radio waves? Does it favor a smaller or larger antenna?
22. Laser vision correction often uses an excimer laser that produces 193-nm electromagnetic radiation. This wavelength is extremely strongly absorbed by the cornea and ablates it in a manner that reshapes the cornea to correct vision defects. Explain how the strong absorption helps concentrate the energy in a thin layer and thus give greater accuracy in shaping the cornea. Also explain how this strong absorption limits damage to the lens and retina of the eye.
Problems & Exercises
24.1: Maxwell’s Equations: Electromagnetic Waves Predicted and Observed
23. Verify that the correct value for the speed of light c is obtained when numerical values for the permeability and permittivity of free space (\(\displaystyle mu_{0}\) and \(\displaystyle \epsilon_{0}\)) are entered into the equation \(\displaystyle c = \frac{1}{\mu_{0}\epsilon_{0}}\).
24. Show that, when SI units for \(\displaystyle \mu_{0}\) and \(\displaystyle \epsilon_{0}\) are entered, the units given by the right-hand side of the equation in the problem above are m/s.
24.2: Production of Electromagnetic Waves
25. What is the maximum electric field strength in an electromagnetic wave that has a maximum magnetic field strength of \(\displaystyle 5.00 \times 10^{-4} T\) (about 10 times the Earth’s)?
Solution
150 kV/m
26. The maximum magnetic field strength of an electromagnetic field is \(\displaystyle 5 \times 10^{-6} T\). Calculate the maximum electric field strength if the wave is traveling in a medium in which the speed of the wave is \(\displaystyle 0.75c\).
27. Verify the units obtained for magnetic field strength \(\displaystyle B\) in the in-chapter example (using the equation \(\displaystyle B = \frac{E}{c}\)) are in fact teslas (T).
24.3: The Electromagnetic Spectrum
28. (a) Two microwave frequencies are authorized for use in microwave ovens: 900 and 2560 MHz. Calculate the wavelength of each.
(b) Which frequency would produce smaller hot spots in foods due to interference effects?
Solution
(a) 33.3 cm (900 MHz) 11.7 cm (2560 MHz)
(b) The microwave oven with the smaller wavelength would produce smaller hot spots in foods, corresponding to the one with the frequency 2560 MHz.
29. (a) Calculate the range of wavelengths for AM radio given its frequency range is 540 to 1600 kHz.
(b) Do the same for the FM frequency range of 88.0 to 108 MHz.
30. A radio station utilizes frequencies between commercial AM and FM. What is the frequency of a 11.12-m-wavelength channel?
Solution
26.96 MHz
31. Find the frequency range of visible light, given that it encompasses wavelengths from 380 to 760 nm.
32. Combing your hair leads to excess electrons on the comb. How fast would you have to move the comb up and down to produce red light?
Solution
\(\displaystyle 5.0 \times 10^{14}\) Hz
33. Electromagnetic radiation having a \(\displaystyle 15.0 - \mu m\) wavelength is classified as infrared radiation. What is its frequency?
34. Approximately what is the smallest detail observable with a microscope that uses ultraviolet light of frequency \(\displaystyle 1.20 \times 10^{15} Hz\)?
Solution
\(\displaystyle \lambda = \frac{c}{f} = \frac{3.00 \times 10^{8} m/s}{1.20 \times 10^{15} Hz} = 2.50 \times 10^{-7} m\)
35. A radar used to detect the presence of aircraft receives a pulse that has reflected off an object \(\displaystyle 6 \times 10^{-5} s\) after it was transmitted. What is the distance from the radar station to the reflecting object?
36. Some radar systems detect the size and shape of objects such as aircraft and geological terrain. Approximately what is the smallest observable detail utilizing 500-MHz radar?
Solution
0.600 m
37. Determine the amount of time it takes for X-rays of frequency \(\displaystyle 3 \times 10^{18} Hz\) to travel (a) 1 mm and (b) 1 cm.
38. If you wish to detect details of the size of atoms (about \(\displaystyle 1 \times 10^{-10} m\)) with electromagnetic radiation, it must have a wavelength of about this size.
(a) What is its frequency?
(b) What type of electromagnetic radiation might this be?
Solution
(a) \(\displaystyle f = \frac{c}{\lambda} = \frac{3.00 \times 10^{8} m/s}{1 \times 10^{-10} m} = 3 \times 10^{18} Hz\)
(b) X-rays
39. If the Sun suddenly turned off, we would not know it until its light stopped coming. How long would that be, given that the Sun is \(\displaystyle 1.50 \times 10^{11} m\) away?
40. Distances in space are often quoted in units of light years, the distance light travels in one year.
(a) How many meters is a light year?
(b) How many meters is it to Andromeda, the nearest large galaxy, given that it is \(\displaystyle 2.00 \times 10^{6}\) light years away?
(c) The most distant galaxy yet discovered is \(\displaystyle 12.0 \times 10^{9}\) light years away. How far is this in meters?
41. A certain 50.0-Hz AC power line radiates an electromagnetic wave having a maximum electric field strength of 13.0 kV/m.
(a) What is the wavelength of this very low frequency electromagnetic wave?
(b) What is its maximum magnetic field strength?
Solution
(a) \(\displaystyle 6.00 \times 10^{6} m\)
(b) \(\displaystyle 4.33 \times 10^{-5} T\)
42. During normal beating, the heart creates a maximum 4.00-mV potential across 0.300 m of a person’s chest, creating a 1.00-Hz electromagnetic wave.
(a) What is the maximum electric field strength created?
(b) What is the corresponding maximum magnetic field strength in the electromagnetic wave?
(c) What is the wavelength of the electromagnetic wave?
43. (a) The ideal size (most efficient) for a broadcast antenna with one end on the ground is one-fourth the wavelength (\(\displaystyle \lambda / 4 \) of the electromagnetic radiation being sent out. If a new radio station has such an antenna that is 50.0 m high, what frequency does it broadcast most efficiently? Is this in the AM or FM band?
(b) Discuss the analogy of the fundamental resonant mode of an air column closed at one end to the resonance of currents on an antenna that is one-fourth their wavelength.
Solution
(a) \(\displaystyle 1.50 \times 10^{6} Hz\), AM band
(b) The resonance of currents on an antenna that is 1/4 their wavelength is analogous to the fundamental resonant mode of an air column closed at one end, since the tube also has a length equal to 1/4 the wavelength of the fundamental oscillation.
44. (a) What is the wavelength of 100-MHz radio waves used in an MRI unit?
(b) If the frequencies are swept over a \(\displaystyle +/- 1.00\) range centered on 100 MHz, what is the range of wavelengths broadcast?
45. (a) What is the frequency of the 193-nm ultraviolet radiation used in laser eye surgery?
(b) Assuming the accuracy with which this EM radiation can ablate the cornea is directly proportional to wavelength, how much more accurate can this UV be than the shortest visible wavelength of light?
Solution
(a) \(\displaystyle 1.55 \times 10^{15} Hz\)
(b) The shortest wavelength of visible light is 380 nm, so that \[\frac{\lambda_{visible}}{\lambda_{UV}}\] \[= \frac{380 nm}{193 nm}\] \[= 1.97.\] In other words, the UV radiation is 97% more accurate than the shortest wavelength of visible light, or almost twice as accurate!
46. TV-reception antennas for VHF are constructed with cross wires supported at their centers, as shown in Figure 15 The ideal length for the cross wires is one-half the wavelength to be received, with the more expensive antennas having one for each channel. Suppose you measure the lengths of the wires for particular channels and find them to be 1.94 and 0.753 m long, respectively. What are the frequencies for these channels?
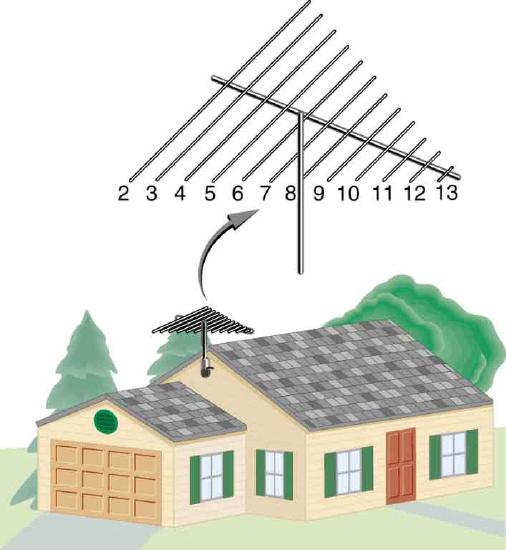
A television reception antenna has cross wires of various lengths to most efficiently receive different wavelengths.
47. Conversations with astronauts on lunar walks had an echo that was used to estimate the distance to the Moon. The sound spoken by the person on Earth was transformed into a radio signal sent to the Moon, and transformed back into sound on a speaker inside the astronaut’s space suit. This sound was picked up by the microphone in the space suit (intended for the astronaut’s voice) and sent back to Earth as a radio echo of sorts. If the round-trip time was 2.60 s, what was the approximate distance to the Moon, neglecting any delays in the electronics?
Solution
\(\displaystyle 3.90 \times 10^{8} m\)
48. Lunar astronauts placed a reflector on the Moon’s surface, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time.
(a) To what accuracy in meters can the distance to the Moon be determined, if this time can be measured to 0.100 ns?
(b) What percent accuracy is this, given the average distance to the Moon is \(\displaystyle 3.84 \times 10^{8} m\)?
49. Radar is used to determine distances to various objects by measuring the round-trip time for an echo from the object.
(a) How far away is the planet Venus if the echo time is 1000 s?
(b) What is the echo time for a car 75.0 m from a Highway Police radar unit?
(c) How accurately (in nanoseconds) must you be able to measure the echo time to an airplane 12.0 km away to determine its distance within 10.0 m?
Solution
(a) \(\displaystyle 1.50 \times 10^{11} m\)
(b) \(\displaystyle 0.500 \mu s\)
(c) 66.7 ns
50. Integrated Concepts:
(a) Calculate the ratio of the highest to lowest frequencies of electromagnetic waves the eye can see, given the wavelength range of visible light is from 380 to 760 nm.
(b) Compare this with the ratio of highest to lowest frequencies the ear can hear.
51. Integrated Concepts:
(a) Calculate the rate in watts at which heat transfer through radiation occurs (almost entirely in the infrared) from \(\displaystyle 1.0 m^{2}\) of the Earth’s surface at night. Assume the emissivity is 0.90, the temperature of the Earth is \(\displaystyle 15^{\circ}C\), and that of outer space is 2.7 K.
(b) Compare the intensity of this radiation with that coming to the Earth from the Sun during the day, which averages about \(\displaystyle 800 W/m^{2}\), only half of which is absorbed.
(c) What is the maximum magnetic field strength in the outgoing radiation, assuming it is a continuous wave?
Solution
(a) \(\displaystyle -3.5 \times 10^{2} W/m^{2}\)
(b) 88%
(c) \(\displaystyle 1.7 \mu T\)
24.4: Energy in Electromagnetic Waves
52. What is the intensity of an electromagnetic wave with a peak electric field strength of 125 V/m?
Solution
\(\displaystyle I = \frac{c \epsilon_{0} E_{0}^{2}}{2}\)
\(\displaystyle = \frac{\left( 3.00 \times 10^{8} m/s \right) \left( 8.85 \times 10^{-12} C^{2} / N \cdot m^{2} \right) \left(125 V/m \right) ^{2}}{2}\)
\(\displaystyle = 20.7 W/m^{2}\)
53. Find the intensity of an electromagnetic wave having a peak magnetic field strength of \(\displaystyle 4.00 \times 10^{-9} T\).
54. Assume the helium-neon lasers commonly used in student physics laboratories have power outputs of 0.250 mW.
(a) If such a laser beam is projected onto a circular spot 1.00 mm in diameter, what is its intensity?
(b) Find the peak magnetic field strength.
(c) Find the peak electric field strength.
Solution
(a) \(\displaystyle I = \frac{P}{A} = \frac{P}{\pi r^{2}} = \frac{0.250 \times 10^{-3} W}{ \pi \left( 0.500 \times 10^{-3} m \right) ^{2}} = 318 W/m^{2}\)
\(\displaystyle I_{ave} = \frac{c B_{0}^{2}}{2 \mu_{0}} \rightarrow B_{0} = \left( \frac{2 \mu_{0}}{c}\right)^{1/2}\)
(b) \(\displaystyle = \left( \frac{2 \left(2 \pi \times 10^{-7} T \cdot m/A \right) \left( 318.3 W/m^{2} \right)}{ 3.00 \times 10^{8} m/s} \right) ^{1/2} \)
\(\displaystyle = 1.63 \times 10^{-6} T\)
(c) \(\displaystyle E_{0} = c B_{0} = \left( 3.00 \times 10^{8} m/s \right) \left(1.633 \times 10^{-6} T \right)\)
\(\displaystyle = 4.90 \times 10^{2} V/m\)
55. An AM radio transmitter broadcasts 50.0 kW of power uniformly in all directions.
(a) Assuming all of the radio waves that strike the ground are completely absorbed, and that there is no absorption by the atmosphere or other objects, what is the intensity 30.0 km away? (Hint: Half the power will be spread over the area of a hemisphere.)
(b) What is the maximum electric field strength at this distance?
56. Suppose the maximum safe intensity of microwaves for human exposure is taken to be \(\displaystyle 1.00 W/m^{2}\).
(a) If a radar unit leaks 10.0 W of microwaves (other than those sent by its antenna) uniformly in all directions, how far away must you be to be exposed to an intensity considered to be safe? Assume that the power spreads uniformly over the area of a sphere with no complications from absorption or reflection.
(b) What is the maximum electric field strength at the safe intensity? (Note that early radar units leaked more than modern ones do. This caused identifiable health problems, such as cataracts, for people who worked near them.)
Solution
(a) 89.2 cm
(b) 27.4 V/m
57. A 2.50-m-diameter university communications satellite dish receives TV signals that have a maximum electric field strength (for one channel) of \(\displaystyle 7.50 \mu V/m\). (See the figure.) (a) What is the intensity of this wave? (b) What is the power received by the antenna? (c) If the orbiting satellite broadcasts uniformly over an area of \(\displaystyle 1.50 \times 10^{13} m^{2}\) (a large fraction of North America), how much power does it radiate?
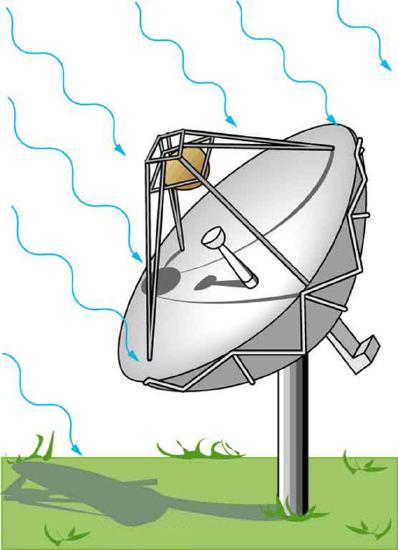
Satellite dishes receive TV signals sent from orbit. Although the signals are quite weak, the receiver can detect them by being tuned to resonate at their frequency.
58. Lasers can be constructed that produce an extremely high intensity electromagnetic wave for a brief time -- called pulsed lasers. They are used to ignite nuclear fusion, for example. Such a laser may produce an electromagnetic wave with a maximum electric field strength of \(\displaystyle 1.00 \times 10^{11} V/m\) for a time of 1.00 ns.
(a) What is the maximum magnetic field strength in the wave?
(b) What is the intensity of the beam?
(c) What energy does it deliver on a \(\displaystyle 1.00 - mm^{2}\) area?
Solution
(a) 333 T
(b) \(\displaystyle 1.33 \times 10^{19} W/m^{2}\)
(c) 13.3 kJ
59. Show that for a continuous sinusoidal electromagnetic wave, the peak intensity is twice the average intensity (\(\displaystyle I_{0} = 2I_{ave}\)), using either the fact that \(\displaystyle E_{0} = \sqrt{2}E_{rms}\), or \(\displaystyle B_{0} = \sqrt{2}B_{rms}\), where rms means average (actually root mean square, a type of average).
60. Suppose a source of electromagnetic waves radiates uniformly in all directions in empty space where there are no absorption or interference effects.
(a) Show that the intensity is inversely proportional to \(\displaystyle r^{2}\), the distance from the source squared.
(b) Show that the magnitudes of the electric and magnetic fields are inversely proportional to \(\displaystyle r\).
Solution
(a) \(\displaystyle I = \frac{P}{A} = \frac{P}{4 \pi r^{2}} \propto \frac{1}{r^{2}}\)
(b) \(\displaystyle I \propto E_{0}^{2}, B_{0}^{2} \rightarrow E_{0}^{2}, B_{0}^{2} \propto \frac{1}{r^{2}} \rightarrow E_{0}, B_{0} \propto \frac{1}{r}\)
61. Integrated Concepts
An \(\displaystyle LC\) circuit with a 5.00-pF capacitor oscillates in such a manner as to radiate at a wavelength of 3.30 m.
(a) What is the resonant frequency?
(b) What inductance is in series with the capacitor?
62. Integrated Concepts
What capacitance is needed in series with an \(\displaystyle 800 - \mu H\) inductor to form a circuit that radiates a wavelength of 196 m?
Solution
13.5 pF
63. Integrated Concepts
Police radar determines the speed of motor vehicles using the same Doppler-shift technique employed for ultrasound in medical diagnostics. Beats are produced by mixing the double Doppler-shifted echo with the original frequency. If \(\displaystyle 1.50 \times 10^{9} - Hz\) microwaves are used and a beat frequency of 150 Hz is produced, what is the speed of the vehicle? (Assume the same Doppler-shift formulas are valid with the speed of sound replaced by the speed of light.)
64. Integrated Concepts:
Assume the mostly infrared radiation from a heat lamp acts like a continuous wave with wavelength \(\displaystyle 1.50 \mu m\).
(a) If the lamp’s 200-W output is focused on a person’s shoulder, over a circular area 25.0 cm in diameter, what is the intensity in \(\displaystyle W/m^{12}\)?
(b) What is the peak electric field strength?
(c) Find the peak magnetic field strength.
(d) How long will it take to increase the temperature of the 4.00-kg shoulder by \(\displaystyle 2.00^{\circ}C\), assuming no other heat transfer and given that its specific heat is \(\displaystyle 3.47 \times 10^{3} J/kg \cdot ^{\circ}C\)?
Solution
(a) \(\displaystyle 4.07 kW/m^{2}\)
(b) 1.75 kV/m
(c) \(\displaystyle 5.84 \mu T\)
(d) 2 min 19 s
65. Integrated Concepts:
On its highest power setting, a microwave oven increases the temperature of 0.400 kg of spaghetti by \(\displaystyle 45.0^{\circ}C\) in 120 s.
(a) What was the rate of power absorption by the spaghetti, given that its specific heat is \(\displaystyle 3.76 \times 10^{3} J/kg \cdot ^{\circ}C\)?
(b) Find the average intensity of the microwaves, given that they are absorbed over a circular area 20.0 cm in diameter.
(c) What is the peak electric field strength of the microwave? (d) What is its peak magnetic field strength?
66. Integrated Concepts:
Electromagnetic radiation from a 5.00-mW laser is concentrated on a \(\displaystyle 1.00 - mm^{2}\) area.
(a) What is the intensity in \(\displaystyle W/ m^{2}\)?
(b) Suppose a 2.00-nC static charge is in the beam. What is the maximum electric force it experiences?
(c) If the static charge moves at 400 m/s, what maximum magnetic force can it feel?
Solution
(a) \(\displaystyle 5.00 \times 10^{3} W/m^{2}\)
(b) \(\displaystyle 3.88 \times 10^{-6} N\)
(c)\(\displaystyle 5.18 \times 10^{-12} N\)
67. Integrated Concepts:
A 200-turn flat coil of wire 30.0 cm in diameter acts as an antenna for FM radio at a frequency of 100 MHz. The magnetic field of the incoming electromagnetic wave is perpendicular to the coil and has a maximum strength of \(\displaystyle 1.00 \times 10^{-12} T\).
(a) What power is incident on the coil?
(b) What average emf is induced in the coil over one-fourth of a cycle?
(c) If the radio receiver has an inductance of \(\displaystyle 2.50 \mu H\), what capacitance must it have to resonate at 100 MHz?
68. Integrated Concepts:
If electric and magnetic field strengths vary sinusoidally in time, being zero at \(\displaystyle t = 0\), then \(\displaystyle E = E_{0} \sin{2 \pi} ft\) and \(\displaystyle B = B_{0} \sin{2 \pi} ft\). Let \(\displaystyle f = 1.00 GHz\) here.
(a) When are the field strengths first zero?
(b) When do they reach their most negative value?
(c) How much time is needed for them to complete one cycle?
Solution
(a) \(\displaystyle t = 0\)
(b) \(\displaystyle 7.50 \times 10^{-10} s\)
(c) \(\displaystyle 1.00 \times 10^{-9} s\)
69. Unreasonable Results:
A researcher measures the wavelength of a 1.20-GHz electromagnetic wave to be 0.500 m.
(a) Calculate the speed at which this wave propagates.
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
70. Unreasonable Results:
The peak magnetic field strength in a residential microwave oven is \(\displaystyle 9.20 \times 10^{-5} T\).
(a) What is the intensity of the microwave?
(b) What is unreasonable about this result?
(c) What is wrong about the premise?
Solution
(a) \(\displaystyle 1.01 \times 10^{6} W/m^{2}\)
(b) Much too great for an oven.
(c) The assumed magnetic field is unreasonably large.
71. Unreasonable Results:
An \(\displaystyle LC\) circuit containing a 2.00-H inductor oscillates at such a frequency that it radiates at a 1.00-m wavelength.
(a) What is the capacitance of the circuit?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
72. Unreasonable Results:
An \(\displaystyle LC\) circuit containing a 1.00-pF capacitor oscillates at such a frequency that it radiates at a 300-nm wavelength.
(a) What is the inductance of the circuit?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) \(\displaystyle 2.53 \times 10^{-20} H\)
(b) L is much too small.
(c) The wavelength is unreasonably small.
73. Create Your Own Problem:
Consider electromagnetic fields produced by high voltage power lines. Construct a problem in which you calculate the intensity of this electromagnetic radiation in \(\displaystyle W/m^{2}\) based on the measured magnetic field strength of the radiation in a home near the power lines. Assume these magnetic field strengths are known to average less than a \(\displaystyle \mu T\). The intensity is small enough that it is difficult to imagine mechanisms for biological damage due to it. Discuss how much energy may be radiating from a section of power line several hundred meters long and compare this to the power likely to be carried by the lines. An idea of how much power this is can be obtained by calculating the approximate current responsible for \(\displaystyle \mu T\) fields at distances of tens of meters.
74. Create Your Own Problem:
Consider the most recent generation of residential satellite dishes that are a little less than half a meter in diameter. Construct a problem in which you calculate the power received by the dish and the maximum electric field strength of the microwave signals for a single channel received by the dish. Among the things to be considered are the power broadcast by the satellite and the area over which the power is spread, as well as the area of the receiving dish.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


