10.3: Dynamics of Rotational Motion - Rotational Inertia
- Page ID
- 1554
Learning Objectives
By the end of this section, you will be able to:
- Understand the relationship between force, mass and acceleration.
- Study the turning effect of force.
- Study the analogy between force and torque, mass and moment of inertia, and linear acceleration and angular acceleration.
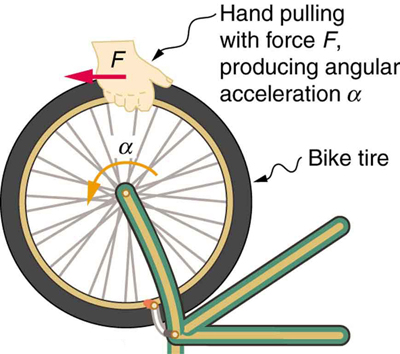
If you have ever spun a bike wheel or pushed a merry-go-round, you know that force is needed to change angular velocity as seen in Figure 10.4.1. In fact, your intuition is reliable in predicting many of the factors that are involved. For example, we know that a door opens slowly if we push too close to its hinges. Furthermore, we know that the more massive the door, the more slowly it opens. The first example implies that the farther the force is applied from the pivot, the greater the angular acceleration; another implication is that angular acceleration is inversely proportional to mass. These relationships should seem very similar to the familiar relationships among force, mass, and acceleration embodied in Newton’s second law of motion. There are, in fact, precise rotational analogs to both force and mass.
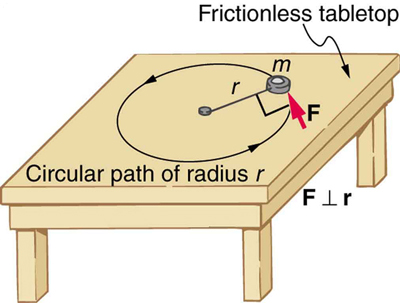
To develop the precise relationship among force, mass, radius, and angular acceleration, consider what happens if we exert a force \(F\) on a point mass \(m\) that is at a distance \(r\) from a pivot point, as shown in Figure 10.4.2. Because the force is perpendicular to \(r\), an accelerationn\(a = frac{F}{m}\) is obtained in the direction of \(F\). We can rearrange this equation such that \(F = ma\) and then look for ways to relate this expression to expressions for rotational quantities. We note that \(a = r\alpha\), and we substitute this expression into \(F = ma\), yielding \[F = mr\alpha.\] Recall that torque is the turning effectiveness of a force. In this case, because \(F\) is perpendicular to \(r\), torque is simply \(\tau = Fr\). So, if we multiply both sides of the equation above by \(r\), we get torque on the left-hand side. That is, \[rF = mr^2\alpha\] or \[\tau = mr^2\alpha.\]
This last equation is the rotational analog of Newton’s second law \(F = ma\), where torque is analogous to force, angular acceleration is analogous to translational acceleration, and \(mr^2\) is analogous to mass (or inertia). The quantity \(mr^2\) is called the rotational inertia or moment of inertia of a point mass \(m\) a distance \(r\) from the center of rotation.
Making Connections: Rotational Motion Dynamics
Dynamics for rotational motion is completely analogous to linear or translational dynamics. Dynamics is concerned with force and mass and their effects on motion. For rotational motion, we will find direct analogs to force and mass that behave just as we would expect from our earlier experiences.
Rotational Inertia and Moment of Inertia
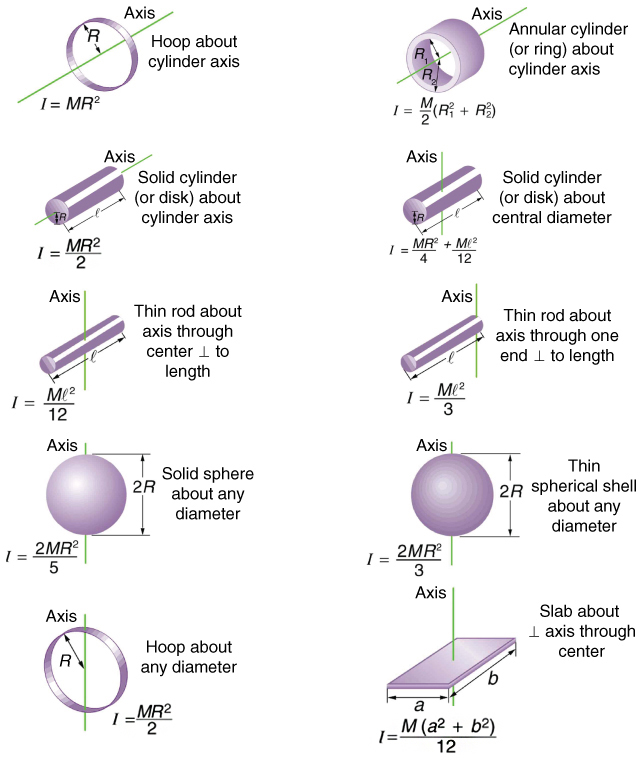
Before we can consider the rotation of anything other than a point mass like the one in Figure, we must extend the idea of rotational inertia to all types of objects. To expand our concept of rotational inertia, we define the moment of inertia \(I\) of an object to be the sum of \(mr^2\) for all the point masses of which it is composed. That is, \(I = \sum mr^2\). Here \(I\) is analogous to \(m\) in translational motion. Because of the distance \(r\), the moment of inertia for any object depends on the chosen axis. Actually, calculating \(I\) is beyond the scope of this text except for one simple case—that of a hoop, which has all its mass at the same distance from its axis. A hoop’s moment of inertia around its axis is therefore \(MR^2\), where \(M\) is its total mass and \(R\) its radius. (We use \(M\) and \(R\) for an entire object to distinguish them from \(m\) and \(r\) for point masses.) In all other cases, we must consult Figure 10.4.3 (note that the table is piece of artwork that has shapes as well as formulae) for formulas for \(I\) that have been derived from integration over the continuous body. Note that \(I\) has units of mass multiplied by distance squared \((kg \cdot m^2)\) as we might expect from its definition.
The general relationship among torque, moment of inertia, and angular acceleration is \[net \, \tau = I \alpha\] or \[\alpha = \dfrac{net \, \tau}{I},\] where net \(\tau\) is the total torque from all forces relative to a chosen axis. For simplicity, we will only consider torques exerted by forces in the plane of the rotation. Such torques are either positive or negative and add like ordinary numbers. The relationship in \(\tau = I\alpha\), \(\alpha = \frac{net \, \tau}{I}\) is the rotational analog to Newton’s second law and is very generally applicable. This equation is actually valid for any torque, applied to any object, relative to any axis.
As we might expect, the larger the torque is, the larger the angular acceleration is. For example, the harder a child pushes on a merry-go-round, the faster it accelerates. Furthermore, the more massive a merry-go-round, the slower it accelerates for the same torque. The basic relationship between moment of inertia and angular acceleration is that the larger the moment of inertia, the smaller is the angular acceleration. But there is an additional twist. The moment of inertia depends not only on the mass of an object, but also on its distribution of mass relative to the axis around which it rotates. For example, it will be much easier to accelerate a merry-go-round full of children if they stand close to its axis than if they all stand at the outer edge. The mass is the same in both cases; but the moment of inertia is much larger when the children are at the edge.
Take-Home Experiment
- Cut out a circle that has about a 10 cm radius from stiff cardboard. Near the edge of the circle, write numbers 1 to 12 like hours on a clock face. Position the circle so that it can rotate freely about a horizontal axis through its center, like a wheel. (You could loosely nail the circle to a wall.) Hold the circle stationary and with the number 12 positioned at the top, attach a lump of blue putty (sticky material used for fixing posters to walls) at the number 3. How large does the lump need to be to just rotate the circle? Describe how you can change the moment of inertia of the circle. How does this change affect the amount of blue putty needed at the number 3 to just rotate the circle? Change the circle’s moment of inertia and then try rotating the circle by using different amounts of blue putty. Repeat this process several times.
Problem-Solving Strategy for Rotational Dynamics
- Examine the situation to determine that torque and mass are involved in the rotation. Draw a careful sketch of the situation.
- Determine the system of interest.
- Draw a free body diagram. That is, draw and label all external forces acting on the system of interest.
- Apply \(net \, \tau = \alpha\), \(\alpha = \frac{net \, \tau}{I},\)
- the rotational equivalent of Newton’s second law, to solve the problem. Care must be taken to use the correct moment of inertia and to consider the torque about the point of rotation.
- As always, check the solution to see if it is reasonable.
Making Connections: Statics vs. Kinetics
In statics, the net torque is zero, and there is no angular acceleration. In rotational motion, net torque is the cause of angular acceleration, exactly as in Newton’s second law of motion for rotation.
Example \(\PageIndex{1}\): Calculating the Effect of Mass Distribution
Consider the father pushing a playground merry-go-round in Figure. He exerts a force of 250 N at the edge of the 50.0-kg merry-go-round, which has a 1.50 m radius. Calculate the angular acceleration produced (a) when no one is on the merry-go-round and (b) when an 18.0-kg child sits 1.25 m away from the center. Consider the merry-go-round itself to be a uniform disk with negligible retarding friction.
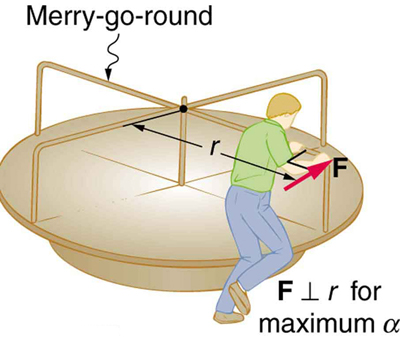
Strategy
Angular acceleration is given directly by the expression \(\alpha = \frac{net \, \tau}{I}\) \[\alpha = \dfrac{\tau}{I}.\] To solve for \(\alpha\), we must first calculate the torque (which is the same in both cases) and moment of inertia \(I\) (which is greater in the second case). To find the torque, we note that the applied force is perpendicular to the radius and friction is negligible, so that\[\tau = rF \, sin \, \theta = (1.50 \, m)(250 \, N) = 375 \, N \cdot m.\]
Solution for (a)
The moment of inertia of a solid disk about this axis is given in Figure to be \[\dfrac{1}{2}MR^2,\] where \(M = 50.0 \, kg\) and \(R = 1.50 \, m\), so that
\[I = (0.500)(50.0 \, kg)(1.50 \, m)^2 = 56.25 \, kg \cdot m^2\]
Now, after we substitute the known values, we find the angular acceleration to be
\[\alpha = \dfrac{\tau}{I} = \dfrac{375 \, N \cdot m}{56.25 \, kg \cdot m^2} = 6.67 \dfrac{rad}{s^2}.\]
Solution for (b)
We expect the angular acceleration for the system to be less in this part, because the moment of inertia is greater when the child is on the merry-go-round. To find the total moment of inertia \(I\), we first find the child’s moment of inertia \(I_c\) by considering the child to be equivalent to a point mass at a distance of 1.25 m from the axis. Then,
\[I_c = MR^2 = (18.0 \, kg)(1.25 \, m)^2 = 28.13 \, kg \cdot m^2.\]
The total moment of inertia is the sum of moments of inertia of the merry-go-round and the child (about the same axis). To justify this sum to yourself, examine the definition of \(I\):
\[I = 28.13 \, kg \cdot m^2 + 56.25 \, kg \cdot m^2 = 84.38 \, kg \cdot m^2.\]
Substituting known values into the equation for \(\alpha \) gives
\[\alpha = \dfrac{\tau}{I} = \dfrac{375 \, N \cdot m}{84.38 \, kg \cdot m^2} = 4.44 \dfrac{rad}{s^2}.\]
Discussion
The angular acceleration is less when the child is on the merry-go-round than when the merry-go-round is empty, as expected. The angular accelerations found are quite large, partly due to the fact that friction was considered to be negligible. If, for example, the father kept pushing perpendicularly for 2.00 s, he would give the merry-go-round an angular velocity of 13.3 rad/s when it is empty but only 8.89 rad/s when the child is on it. In terms of revolutions per second, these angular velocities are 2.12 rev/s and 1.41 rev/s, respectively. The father would end up running at about 50 km/h in the first case. Summer Olympics, here he comes! Confirmation of these numbers is left as an exercise for the reader.
Exercise \(\PageIndex{1}\):Check Your Understanding
Torque is the analog of force and moment of inertia is the analog of mass. Force and mass are physical quantities that depend on only one factor. For example, mass is related solely to the numbers of atoms of various types in an object. Are torque and moment of inertia similarly simple?
No. Torque depends on three factors: force magnitude, force direction, and point of application. Moment of inertia depends on both mass and its distribution relative to the axis of rotation. So, while the analogies are precise, these rotational quantities depend on more factors
Summary
- The farther the force is applied from the pivot, the greater is the angular acceleration; angular acceleration is inversely proportional to mass.
- If we exert a force \(F\) on a point mass \(m\) that is a distance r from a pivot point and because the force is perpendicular to r and acceleration \(a = F/m\) is obtained in the direction of \(F\). We can rearrange this equation such that \[F = ma,\] and then look for ways to relate this expression to expressions for rotational quantities. We note that \(a = r \alpha\), and we substitute this expression into \(F = ma\), yielding \[F = mr\alpha\]
- Torque is the turning effectiveness of a force. In this case, because \(F\) is perpendicular to \(r\), torque is simply \(\tau = rF\). If we multiply both sides of the equation above by \(r\), we get torque on the left-hand side. That is, \[rF = mr^2\alpha\] or \[\tau = mr^2\alpha.\]
- The moment of inertia \(I\) of an object is the sum of \(MR^2\) for all the point masses of which it is composed. That is, \[I = \sum mr^2.\]
- The general relationship among torque, moment of inertia, and angular acceleration is \[\tau = I \alpha\] or \[\alpha = \dfrac{net \, \tau}{I}.\]
Glossary
- torque
- the turning effectiveness of a force
- rotational inertia
- resistance to change of rotation. The more rotational inertia an object has, the harder it is to rotate
- moment of inertia
- mass times the square of perpendicular distance from the rotation axis; for a point mass, it is I=mr2 and, because any object can be built up from a collection of point masses, this relationship is the basis for all other moments of inertia


