01. Concepts and Principles
- Page ID
- 463
An empirical fact about nature is that motion in one direction (for example, the horizontal) does not appear to influence aspects of the motion in a perpendicular direction (the vertical). Imagine a coin dropped from shoulder height. The elapsed time for the coin to hit the ground, the rate at which its vertical position is changing, and its vertical acceleration are the same whether you do this experiment in a stationary bus or one traveling down a smooth, level highway at 65 mph. The horizontal motion of the coin does not affect these aspects of its vertical motion.[1]
Thus, to completely describe the motion of an object moving both horizontally and vertically, you can first ignore the horizontal motion, and describe only the vertical component of the motion, and then ignore the vertical motion, and describe the horizontal component. Putting these kinematic components together gives you a complete description of the motion. This experimental fact about nature will make analyzing multi-dimensional motion no more conceptually difficult than analyzing one-dimensional motion.
Given this independence between motions in perpendicular directions, the same kinematic concepts and relationships utilized in one-dimensional motion will be utilized for multi-dimensional motion.
Position (r)
The position of an object is its location relative to a well-defined coordinate system. In multi-dimensional situations, however, you must designate coordinate systems for all perpendicular directions of interest. The zero and positive direction for one dimension is completely independent of the zero and positive direction for another direction. The location at which all coordinate system zeros intersect is referred to as the origin of the coordinate system.
Velocity (v)
The velocity is the rate at which the position is changing. Thus, we will define the velocity component in the vertical direction, for example, as the rate at which the vertical position is changing. The velocity component in the vertical direction is completely independent of the horizontal position or the rate at which the horizontal position changes.
As long as the coordinate directions are perpendicular, the speed, or magnitude of the object’s velocity, can be determined by:
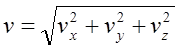
The direction of the object’s velocity can be determined via right-angle trigonometry.
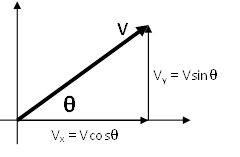
Acceleration (a)
The acceleration is the rate at which the velocity is changing. Thus, we will define the acceleration component in the vertical direction, for example, as the rate at which the velocity component in the vertical direction is changing. The acceleration component in the vertical direction is completely independent of the velocity component in the horizontal direction or the rate at which the velocity component in the horizontal direction changes.
As long as the coordinate directions are perpendicular, the magnitude of the object’s acceleration can always be determined by:

The direction of the object’s acceleration can be determined via right-angle trigonometry
Doing kinematics in multiple dimensions involves a concerted effort on your part to disregard motion in one direction when considering motion in a perpendicular direction. The ability to mentally break down a complicated motion into its component motions requires considerable practice.
[1] Actually, at extremely high speeds the horizontal and vertical motions are not independent. At speeds comparable to the speed of light, the interdependence between horizontal and vertical motion (because of time dilation) becomes noticeable.


