01. Concepts and Principles
- Page ID
- 399
Putting it All Together
Electric charges are surrounded by electric fields. When these charges move, the electric field changes. Additionally, these moving charges (or, more importantly, these changing electric fields) create magnetic fields. Since before the motion no magnetic field existed, this is a change in the value of the magnetic field (from zero to non-zero). By electromagnetic induction, this change in magnetic field creates emf, which is a change in the value of the electric field in a region of space. But this change in electric field must cause further change in the magnetic field, which must cause further change in the electric field, which must...
Sorting through this interrelationship between electric and magnetic fields, which involves the simultaneously solution of a set of coupled, partial-differential equations, is the grand accomplish of James Maxwell. This work of Maxwell's, in the 1860s, is generally regarded as on par with the work of Isaac Newton and Albert Einstein. Although we won't actually solve this set of equations, we will study several of the consequences of Maxwell's work.
Electromagnetic Waves
By far the most important conclusion from Maxwell's work is that the changes in electric and magnetic fields, coupled together as described above, progagate through space as an electromagnetic wave. Near the moving charge that created the wave, the mathematical description of the wave is very complicated, but once the wave has moved a "reasonable" distance from the charge that created it, it can be visualized as below:
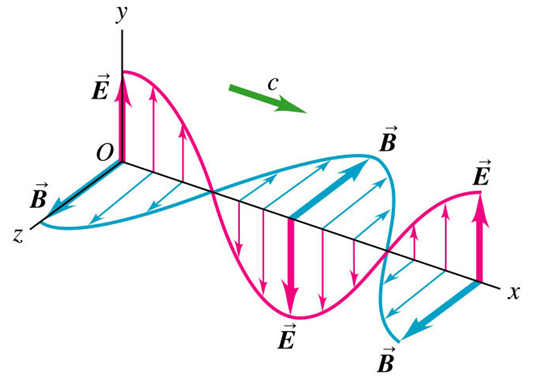
and mathematically represented as:
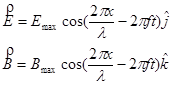
where
- l is the wavelength of the wave, the distance between maximum values of the field vectors,
- f is the frequency of the wave, the number of complete cycles of oscillation that wave passes through per second,
- the electric and magnetic field vectors are perfectly in phase, meaning they pass through their maximum and minimum values at the same points in space and time,
- the field vectors are oriented at 90° from each other,
- and the wave propagates in the directon, given by
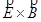 , which in this case is the +x-direction.
, which in this case is the +x-direction.
Of course, a similar mathematical description could be given for an electromagnetic wave propagating in any direction.
It's important to realize that the "picture" of the wave above is for a specific instant of time. This is a traveling wave, in that it moves through space, in this case in the +x-direction. Since it moves through space, an important characteristic of the wave is its speed. While solving the set of equations, Maxwell found that the speed of electromagnetic waves, denoted c, is given by the expression:
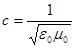
where e0 and m0 are the familiar permittivity and permeability of free space.
What is somewhat odd about this result is that it states that the speed of the wave is a universal constant, since both e0 and m0 are constant. This means that regardless of the wavelength of the wave, or its frequency, or whether the charges that created the wave were wiggling in a stationary radio antenna on top of a mountain or in the headlight of a spaceship moving at a billion miles per hour (or if you viewed the wave from a second spaceship moving a billion mph in the other direction!) the wave always moves at exactly the same speed. The wave speed is completely independent of how it was created. Once the wave is created, its motion through space is completely determined by how its electric and magnetic fields interact with each other, and its speed has no relationship to the physical charge that created it. (This fact will have some curious repercussions about 40 years after Maxwell's discovery.)
Plugging in the known values for e0 and m0 yields:
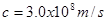
Maxwell realized that this was the known speed for visible light, and soon came to the conclusion that light was, in fact, an electromagnetic wave. Electromagnetic waves of other frequencies, such as radio waves, microwaves, x rays, etc, all propagate at this same speed and obey the same mathematical framework described above.
One final interesting conclusion from Maxwell's solution was that the ratio of the electric field to the magnetic field at any point in the wave has a constant value, equal to the wave speed:
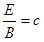
Energy of Electromagnetic Waves
Energy can be stored in electric and magnetic fields, as you learned when you analyzed capacitors and inductors in electric circuits. Since electromagnetic waves involve the propagation of changes in these fields, they should involve the flow of energy in the direction of the wave's motion.
The intensity, or energy flow per unit area, of an electromagnetic wave is given by:
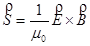
where pic 8 is termed the Poynting vector, and indicates both the direction of the energy flow and its magnitude per unit area. Since the electric and magnetic fields are oriented at 90° from each other, the magnitude of the intensity is given by:
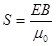
This expression gives you the intensity at any point in the electromagnetic wave at one specific instant of time. However, in many ways this isn't particularly useful. If you are dealingwith a visible light wave, for example, the frequency of the wave is a approximately 1014 cycles per second. This means that the intensity of the wave cycles through maximum and minimum values every 10-14 s!
A much more useful expression would be for the average intensity of the wave. To find this expression, rearrange
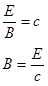
and substitute into the expression for the instantaneous intensity
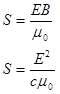
Substituting our description of the electric field-portion of an electromagnetic wave
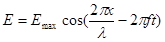
into the above expression yields
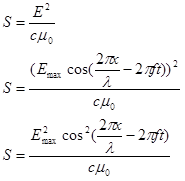
To find the average value of this function we need only to find the average value of the cosine-squared function, since all of the other terms are constant. It's common knowledge[1] that the average value of the cosine-squared function is ½. Therefore, the average intensity of an electromagnetic wave is:
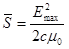
[1]It is now.


