5.12: Force Between the Plates of a Plane Parallel Plate Capacitor
- Page ID
- 6020
We imagine a capacitor with a charge \(+Q\) on one plate and \(-Q\) on the other, and initially the plates are almost, but not quite, touching. There is a force \(F\) between the plates. Now we gradually pull the plates apart (but the separation remains small enough that it is still small compared with the linear dimensions of the plates and we can maintain our approximation of a uniform field between the plates, and so the force remains \(F\) as we separate them). The work done in separating the plates from near zero to \(d\) is \(Fd\), and this must then equal the energy stored in the capacitor, \(\frac{1}{2}QV\). The electric field between the plates is \(E = V/d\), so we find for the force between the plates
\[\label{5.12.1}F=\frac{1}{2}QE.\]
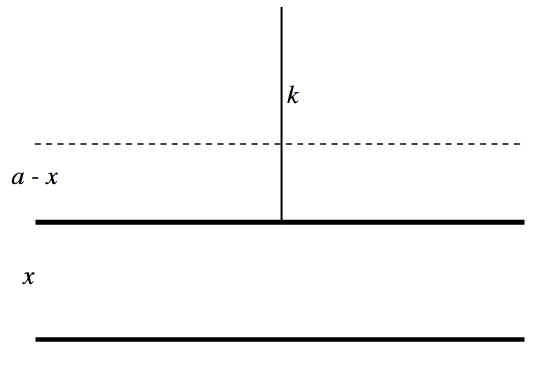
We can now do an interesting imaginary experiment, just to see that we understand the various concepts. Let us imagine that we have a capacitor in which the plates are horizontal; the lower plate is fixed, while the upper plate is suspended above it from a spring of force constant \(k\). We connect a battery across the plates, so the plates will attract each other. The upper plate will move down, but only so far, because the electrical attraction between the plates is countered by the tension in the spring. Calculate the equilibrium separation \(x\) between the plates as a function of the applied voltage \(V\). (Horrid word! We don’t say “metreage” for length, “kilogrammage” for mass or “secondage” for time – so why do we say “voltage” for potential difference and “acreage” for area? Ugh!) We should be able to use our invention as a voltmeter – it even has an infinite resistance! Refer to Figure \(V.\)11.
\(\text{FIGURE V.11}\)
We’ll suppose that the separation when the potential difference is zero is a, and the separation when the potential difference is \(V\) is \(x\), at which time the spring has been extended by a length \(a - x\).
The electrical force between the plates is \(\frac{1}{2}QE\). Now \(Q=CV=\frac{\epsilon_0AV}{x}\text{ and }E=\frac{V}{x}\), so the force between the plates is \(\frac{\epsilon_0AV^2}{2x^2}\). Here \(A\) is the area of each plate and it is assumed that the experiment is done in air, whose permittivity is very close to \(\epsilon_0\). The tension in the stretched spring is \(k(a - x)\), so equating the two forces gives us
\[V^2=\frac{2kx^2(a-x)}{\epsilon_0A}.\label{5.12.2}\]
Calculus shows [do it! – just differentiate \(x^2(1 - x)\)] that \(V\) has a maximum value of \(V_{\text{max}}=\sqrt{\frac{8ka^3}{27\epsilon_0A}}\) for a separation \(x=\frac{2}{3}a\). If we express the potential difference in units of \(V_{\text{max}}\) and the separation in units of \(a\), Equation \ref{5.12.2} becomes
\[\label{5.12.3}V^2=\frac{27x^2(1-x)}{4}.\]
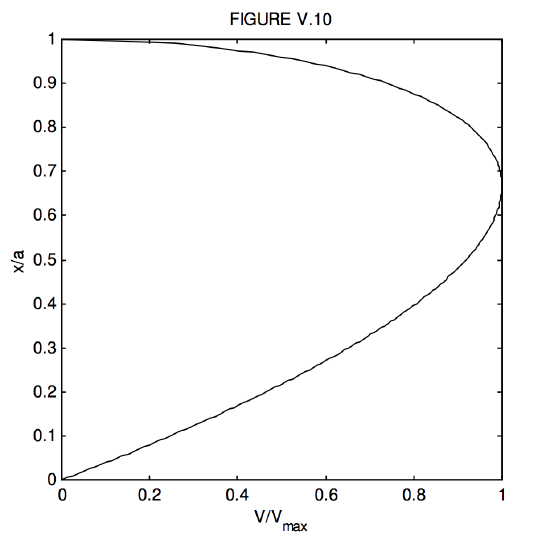
In Figure \(V.\)12 I have plotted the separation as a function of the potential difference.
\(\text{FIGURE V.12}\)
As expected, the potential difference is zero when the separation is 0 or 1 (and therefore you would expect it to go through a maximum for some intermediate separation).
We see that for \(V<V_{\text{max}}\) there are two equilibrium positions. For example, if \(V = 0.8\), show that \(x = 0.396305 \text{ or }0.876617\). The question also arises – what happens if you apply across the plates a potential difference that is greater than \(V\)max?
Further insight can be obtained from energy considerations. The potential energy of the system is the work done in moving the upper plate from \(x = a \text{ to }x = x\) while the potential difference is \(V\):
\[U=\frac{\epsilon_0AV^2}{2a}-\frac{\epsilon_0AV^2}{2x}+\frac{1}{2}k(a-x)^2.\label{5.12.4}\]
You may need to refer to Section 5.15 to be sure that we have got this right.
If we express \(V\) in units of \(V_\text{max}\), \(x\) in units of \(a\), and \(U\) in units of \(ka^2\) this becomes
\[U=\frac{4}{27}V^2(1-1/x)+\frac{1}{2}(1-x)^2\label{5.12.5}\]
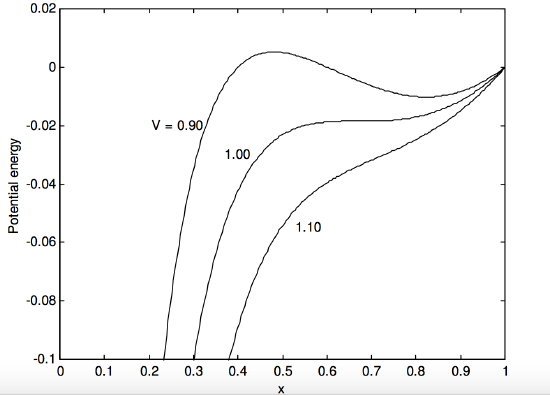
In Figure \(V.\)13 I have plotted the energy versus separation for three values of potential difference, 90% of \(V_\text{max}\), \(V_\text{max}\), and 110% of \(V_\text{max}\).
\(\text{FIGURE V.13}\)
We see that for \(V < V_\text{max}\), there are two equilibrium positions, of which the lower one (smaller x) is unstable, and we see exactly what will happen if the upper plate is displaced slightly upwards (larger \(x\)) from the unstable equilibrium position or if it is displaced slightly downwards (smaller \(x\)). The upper equilibrium position is stable.
If \(V > V_\text{max}\), there is no equilibrium position, and \(x\) goes down to zero – i.e. the plates clamp together.


