2.1: What is Thermodynamics?

$\newcommand\bes{\begin{equation}\begin{split}}$
$\newcommand\ltwid{\propto}$
$\newcommand\ees{\end{split}\end{equation}}$
$\newcommand\mib{\mathbf}$
$\newcommand\Sa{\textsf a}$
$\newcommand\Sb{\textsf b}$
$\newcommand\Sc{\textsf c}$
$\newcommand\Sd{\textsf d}$
$\newcommand\Se{\textsf e}$
$\newcommand\Sf{\textsf f}$
$\newcommand\Sg{\textsf g}$
$\newcommand\Sh{\textsf h}$
$\newcommand\Si{\textsf i}$
$\newcommand\Sj{\textsf j}$
$\newcommand\Sk{\textsf k}$
$\newcommand\Sl{\textsf l}$
$\newcommand\Sm{\textsf m}$
$\newcommand\Sn{\textsf n}$
$\newcommand\So{\textsf o}$
$\newcommand\Sp{\textsf p}$
$\newcommand\Sq{\textsf q}$
$\newcommand\Sr{\textsf r}$
$\newcommand\Ss{\textsf s}$
$\newcommand\St{\textsf t}$
$\newcommand\Su{\textsf u}$
$\newcommand\Sv{\textsf v}$
$\newcommand\Sw{\textsf w}$
$\newcommand\Sx{\textsf x}$
$\newcommand\Sy{\textsf y}$
$\newcommand\Sz{\textsf z}$
$\newcommand\SA{\textsf A}$
$\newcommand\SB{\textsf B}$
$\newcommand\SC{\textsf C}$
$\newcommand\SD{\textsf D}$
$\newcommand\SE{\textsf E}$
$\newcommand\SF{\textsf F}$
$\newcommand\SG{\textsf G}$
$\newcommand\SH{\textsf H}$
$\newcommand\SI{\textsf I}$
$\newcommand\SJ{\textsf J}$
$\newcommand\SK{\textsf K}$
$\newcommand\SL{\textsf L}$
$\newcommand\SM{\textsf M}$
$\newcommand\SN{\textsf N}$
$\newcommand\SO{\textsf O}$
$\newcommand\SP{\textsf P}$
$\newcommand\SQ{\textsf Q}$
$\newcommand\SR{\textsf R}$
$\newcommand\SS{\textsf S}$
$\newcommand\ST{\textsf T}$
$\newcommand\SU{\textsf U}$
$\newcommand\SV{\textsf V}$
$\newcommand\SW{\textsf W}$
$\newcommand\SX{\textsf X}$
$\newcommand\SY{\textsf Y}$
$\newcommand\SZ{\textsf Z}$
$\newcommand\Ha{\hat a}$
$\newcommand\Hb{\hat b}$
$\newcommand\Hc{\hat c}$
$\newcommand\Hd{\hat d}$
$\newcommand\He{\hat e}$
$\newcommand\Hf{\hat f}$
$\newcommand\Hg{\hat g}$
$\newcommand\Hh{\hat h}$
$\newcommand\Hi{\hat \imath}$
$\newcommand\Hj{\hat \jmath}$
$\newcommand\Hk{\hat k}$
$\newcommand\Hl{\hat l}$
$\newcommand\Hm{\hat m}$
$\newcommand\Hn{\hat n}$
$\newcommand\Ho{\hat o}$
$\newcommand\Hp{\hat p}$
$\newcommand\Hq{\hat q}$
$\newcommand\Hr{\hat r}$
$\newcommand\Hs{\hat s}$
$\newcommand\Ht{\hat t}$
$\newcommand\Hu{\hat u}$
$\newcommand\Hv{\hat v}$
$\newcommand\Hw{\hat w}$
$\newcommand\Hx{\hat x}$
$\newcommand\Hy{\hat y}$
$\newcommand\Hz{\hat z}$
$\newcommand\HA{\hat A}$
$\newcommand\HB{\hat B}$
$\newcommand\HC{\hat C}$
$\newcommand\HD{\hat D}$
$\newcommand\HE{\hat E}$
$\newcommand\HF{\hat F}$
$\newcommand\HG{\hat G}$
$\newcommand\HH{\hat H}$
$\newcommand\HI{\hat I}$
$\newcommand\HJ{\hat J}$
$\newcommand\HK{\hat K}$
$\newcommand\HL{\hat L}$
$\newcommand\HM{\hat M}$
$\newcommand\HN{\hat N}$
$\newcommand\HO{\hat O}$
$\newcommand\HP{\hat P}$
$\newcommand\HQ{\hat Q}$
$\newcommand\HR{\hat R}$
$\newcommand\HS{\hat S}$
$\newcommand\HT{\hat T}$
$\newcommand\HU{\hat U}$
$\newcommand\HV{\hat V}$
$\newcommand\HW{\hat W}$
$\newcommand\HX{\hat X}$
$\newcommand\HY{\hat Y}$
$\newcommand\HZ{\hat Z}$
$\newcommand\Halpha{\hat\alpha}$
$\newcommand\Hbeta{\hat\beta}$
$\newcommand\Hgamma{\hat\gamma}$
$\newcommand\Hdelta{\hat\delta}$
$\newcommand\Hepsilon{\hat\epsilon}$
$\newcommand\Hvarepsilon{\hat\varepsilon}$
$\newcommand\Hzeta{\hat\zeta}$
$\newcommand\Heta{\hat\eta}$
$\newcommand\Htheta{\hat\theta}$
$\newcommand\Hvartheta{\hat\vartheta}$
$\newcommand\Hiota{\hat\iota}$
$\newcommand\Hkappa{\hat\kappa}$
$\newcommand\Hlambda{\hat\lambda}$
$\newcommand\Hmu{\hat\mu}$
$\newcommand\Hnu{\hat\nu}$
$\newcommand\Hxi{\hat\xi}$
$\newcommand\Hom{\hat\omicron}$
$\newcommand\Hpi{\hat\pi}$
$\newcommand\Hvarpi{\hat\varpi}$
$\newcommand\Hrho{\hat\rho}$
$\newcommand\Hvarrho{\hat\varrho}$
$\newcommand\Hsigma{\hat\sigma}$
$\newcommand\Hvarsigma{\hat\varsigma}$
$\newcommand\Htau{\var\tau}$
$\newcommand\Hupsilon{\hat\upsilon}$
$\newcommand\Hphi{\hat\phi}$
$\newcommand\Hvarphi{\hat\varphi}$
$\newcommand\Hchi{\hat\chi}$
$\newcommand\Hxhi{\hat\xhi}$
$\newcommand\Hpsi{\hat\psi}$
$\newcommand\Homega{\hat\omega}$
$\newcommand\HGamma{\hat\Gamma}$
$\newcommand\HDelta{\hat\Delta}$
$\newcommand\HTheta{\hat\Theta}$
$\newcommand\HLambda{\hat\Lambda}$
$\newcommand\HXi{\hat\Xi}$
$\newcommand\HPi{\hat\Pi}$
$\newcommand\HSigma{\hat\Sigma}$
$\newcommand\HUps{\hat\Upsilon}$
$\newcommand\HPhi{\hat\Phi}$
$\newcommand\HPsi{\hat\Psi}$
$\newcommand\HOmega{\hat\Omega}$
$\newcommand\xhat{\hat\Bx}$
$\newcommand\yhat{\hat\By}$
$\newcommand\zhat{\hat\Bz}$
$\newcommand\ehat{\hat\Be}$
$\newcommand\khat{\hat\Bk}$
$\newcommand\nhat{\hat\Bn}$
$\newcommand\rhat{\hat\Br}$
$\newcommand\phihat{\hat\Bphi}$
$\newcommand\thetahat{\hat\Btheta}$
$\newcommand\MA{\mathbb A}$
$\newcommand\MB{\mathbb B}$
$\newcommand\MC{\mathbb C}$
$\newcommand\MD{\mathbb D}$
$\newcommand\ME{\mathbb E}$
$\newcommand\MF{\mathbb F}$
$\newcommand\MG{\mathbb G}$
$\newcommand\MH{\mathbb H}$
$\newcommand\MI{\mathbb I}$
$\newcommand\MJ{\mathbb J}$
$\newcommand\MK{\mathbb K}$
$\newcommand\ML{\mathbb L}$
$\newcommand\MM{\mathbb M}$
$\newcommand\MN{\mathbb N}$
$\newcommand\MO{\mathbb O}$
$\newcommand\MP{\mathbb P}$
$\newcommand\MQ{\mathbb Q}$
$\newcommand\MR{\mathbb R}$
$\newcommand\MS{\mathbb S}$
$\newcommand\MT{\mathbb T}$
$\newcommand\MU{\mathbb U}$
$\newcommand\MV{\mathbb V}$
$\newcommand\MW{\mathbb W}$
$\newcommand\MX{\mathbb X}$
$\newcommand\MY{\mathbb Y}$
$\newcommand\MZ{\mathbb Z}$
$\newcommand\CA{\mathcal A}$
$\newcommand\CB{\mathcal B}$
$\newcommand\CC{\mathcal C}$
$\newcommand\CD{\mathcal D}$
$\newcommand\CE{\mathcal E}$
$\newcommand\CF{\mathcal F}$
$\newcommand\CG{\mathcal G}$
$\newcommand\CH{\mathcal H}$
$\newcommand\CI{\mathcal I}$
$\newcommand\CJ{\mathcal J}$
$\newcommand\CK{\mathcal K}$
$\newcommand\CL{\mathcal L}$
$\newcommand\CM{\mathcal M}$
$\newcommand\CN{\mathcal N}$
$\newcommand\CO{\mathcal O}$
$\newcommand\CP{\mathcal P}$
$\newcommand\CQ{\mathcal Q}$
$\newcommand\CR{\mathcal R}$
$\newcommand\CS{\mathcal S}$
$\newcommand\CT{\mathcal T}$
$\newcommand\CU{\mathcal U}$
$\newcommand\CV{\mathcal V}$
$\newcommand\CW{\mathcal W}$
$\newcommand\CX{\mathcal X}$
$\newcommand\CY{\mathcal Y}$
$\newcommand\CZ{\mathcal Z}$
$\newcommand\Fa{\mathfrak a}$
$\newcommand\Fb{\mathfrak b}$
$\newcommand\Fc{\mathfrak c}$
$\newcommand\Fd{\mathfrak d}$
$\newcommand\Fe{\mathfrak e}$
$\newcommand\Ff{\mathfrak f}$
$\newcommand\Fg{\mathfrak g}$
$\newcommand\Fh{\mathfrak h}$
$\newcommand\Fi{\mathfrak i}$
$\newcommand\Fj{\mathfrak j}$
$\newcommand\Fk{\mathfrak k}$
$\newcommand\Fl{\mathfrak l}$
$\newcommand\Fm{\mathfrak m}$
$\newcommand\Fn{\mathfrak n}$
$\newcommand\Fo{\mathfrak o}$
$\newcommand\Fp{\mathfrak p}$
$\newcommand\Fq{\mathfrak q}$
$\newcommand\Fr{\mathfrak r}$
$\newcommand\Fs{\mathfrak s}$
$\newcommand\Ft{\mathfrak t}$
$\newcommand\Fu{\mathfrak u}$
$\newcommand\Fv{\mathfrak v}$
$\newcommand\Fw{\mathfrak w}$
$\newcommand\Fx{\mathfrak x}$
$\newcommand\Fy{\mathfrak y}$
$\newcommand\Fz{\mathfrak z}$
$\newcommand\FA{\mathfrak A}$
$\newcommand\FB{\mathfrak B}$
$\newcommand\FC{\mathfrak C}$
$\newcommand\FD{\mathfrak D}$
$\newcommand\FE{\mathfrak E}$
$\newcommand\FF{\mathfrak F}$
$\newcommand\FG{\mathfrak G}$
$\newcommand\FH{\mathfrak H}$
$\newcommand\FI{\mathfrak I}$
$\newcommand\FJ{\mathfrak J}$
$\newcommand\FK{\mathfrak K}$
$\newcommand\FL{\mathfrak L}$
$\newcommand\FM{\mathfrak M}$
$\newcommand\FN{\mathfrak N}$
$\newcommand\FO{\mathfrak O}$
$\newcommand\FP{\mathfrak P}$
$\newcommand\FQ{\mathfrak Q}$
$\newcommand\FR{\mathfrak R}$
$\newcommand\FS{\mathfrak S}$
$\newcommand\FT{\mathfrak T}$
$\newcommand\FU{\mathfrak U}$
$\newcommand\FV{\mathfrak V}$
$\newcommand\FW{\mathfrak W}$
$\newcommand\FX{\mathfrak X}$
$\newcommand\FY{\mathfrak Y}$
$\newcommand\FZ{\mathfrak Z}$
$\newcommand\Da{\dot a}$
$\newcommand\Db{\dot b}$
$\newcommand\Dc{\dot c}$
$\newcommand\Dd{\dot d}$
$\newcommand\De{\dot e}$
$\newcommand\Df{\dot f}$
$\newcommand\Dg{\dot g}$
$\newcommand\Dh{\dot h}$
$\newcommand\Di{\dot \imath}$
$\newcommand\Dj{\dot \jmath}$
$\newcommand\Dk{\dot k}$
$\newcommand\Dl{\dot l}$
$\newcommand\Dm{\dot m}$
$\newcommand\Dn{\dot n}$
$\newcommand\Do{\dot o}$
$\newcommand\Dp{\dot p}$
$\newcommand\Dq{\dot q}$
$\newcommand\Dr{\dot r}$
$\newcommand\Ds{\dot s}$
$\newcommand\Dt{\dot t}$
$\newcommand\Du{\dot u}$
$\newcommand\Dv{\dot v}$
$\newcommand\Dw{\dot w}$
$\newcommand\Dx{\dot x}$
$\newcommand\Dy{\dot y}$
$\newcommand\Dz{\dot z}$
$\newcommand\DA{\dot A}$
$\newcommand\DB{\dot B}$
$\newcommand\DC{\dot C}$
$\newcommand\DD{\dot D}$
$\newcommand\DE{\dot E}$
$\newcommand\DF{\dot F}$
$\newcommand\DG{\dot G}$
$\newcommand\DH{\dot H}$
$\newcommand\DI{\dot I}$
$\newcommand\DJ{\dot J}$
$\newcommand\DK{\dot K}$
$\newcommand\DL{\dot L}$
$\newcommand\DM{\dot M}$
$\newcommand\DN{\dot N}$
$\newcommand\DO{\dot O}$
$\newcommand\DP{\dot P}$
$\newcommand\DQ{\dot Q}$
$\newcommand\DR{\dot R}$
$\newcommand\DS{\dot S}$
$\newcommand\DT{\dot T}$
$\newcommand\DU{\dot U}$
$\newcommand\DV{\dot V}$
$\newcommand\DW{\dot W}$
$\newcommand\DX{\dot X}$
$\newcommand\DY{\dot Y}$
$\newcommand\DZ{\dot Z}$
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Dmu{\dot\mu}$
$\newcommand\Dnu{\dot\nu}$
$\newcommand\Dxi{\dot\xi}$
$\newcommand\Dom{\dot\omicron}$
$\newcommand\Dpi{\dot\pi}$
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Drho{\dot\rho}$
$\newcommand\Dvarrho{\dot\varrho}$
$\newcommand\Dsigma{\dot\sigma}$
$\newcommand\Dvarsigma{\dot\varsigma}$
$\newcommand\Dtau{\var\tau}$
$\newcommand\Dupsilon{\dot\upsilon}$
$\newcommand\Dphi{\dot\phi}$
$\newcommand\Dvarphi{\dot\varphi}$
$\newcommand\Dchi{\dot\chi}$
$\newcommand\Dpsi{\dot\psi}$
$\newcommand\Domega{\dot\omega}$
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\DLambda{\dot\Lambda}$
$\newcommand\DXi{\dot\Xi}$
$\newcommand\DPi{\dot\Pi}$
$\newcommand\DSigma{\dot\Sigma}$
$\newcommand\DUps{\dot\Upsilon}$
$\newcommand\DPhi{\dot\Phi}$
$\newcommand\DPsi{\dot\Psi}$
$\newcommand\DOmega{\dot\Omega}$
$\newcommand\Va{\vec a}$
$\newcommand\Vb{\vec b}$
$\newcommand\Vc{\vec c}$
$\newcommand\Vd{\vec d}$
$\newcommand\Ve{\vec e}$
$\newcommand\Vf{\vec f}$
$\newcommand\Vg{\vec g}$
$\newcommand\Vh{\vec h}$
$\newcommand\Vi{\vec \imath}$
$\newcommand\Vj{\vec \jmath}$
$\newcommand\Vk{\vec k}$
$\newcommand\Vl{\vec l}$
$\newcommand\Vm{\vec m}$
$\newcommand\Vn{\vec n}$
$\newcommand\Vo{\vec o}$
$\newcommand\Vp{\vec p}$
$\newcommand\Vq{\vec q}$
$\newcommand\Vr{\vec r}$
$\newcommand\Vs{\vec s}$
$\newcommand\Vt{\vec t}$
$\newcommand\Vu{\vec u}$
$\newcommand\Vv{\vec v}$
$\newcommand\Vw{\vec w}$
$\newcommand\Vx{\vec x}$
$\newcommand\Vy{\vec y}$
$\newcommand\Vz{\vec z}$
$\newcommand\VA{\vec A}$
$\newcommand\VB{\vec B}$
$\newcommand\VC{\vec C}$
$\newcommand\VD{\vec D}$
$\newcommand\VE{\vec E}$
$\newcommand\VF{\vec F}$
$\newcommand\VG{\vec G}$
$\newcommand\VH{\vec H}$
$\newcommand\VI{\vec I}$
$\newcommand\VJ{\vec J}$
$\newcommand\VK{\vec K}$
$\newcommand\VL{\vec L}$
$\newcommand\VM{\vec M}$
$\newcommand\VN{\vec N}$
$\newcommand\VO{\vec O}$
$\newcommand\VP{\vec P}$
$\newcommand\VQ{\vec Q}$
$\newcommand\VR{\vec R}$
$\newcommand\VS{\vec S}$
$\newcommand\VT{\vec T}$
$\newcommand\VU{\vec U}$
$\newcommand\VV{\vec V}$
$\newcommand\VW{\vec W}$
$\newcommand\VX{\vec X}$
$\newcommand\VY{\vec Y}$
$\newcommand\VZ{\vec Z}$
$\newcommand\Valpha{\vec\alpha}$
$\newcommand\Vbeta{\vec\beta}$
$\newcommand\Vgamma{\vec\gamma}$
$\newcommand\Vdelta{\vec\delta}$
$\newcommand\Vepsilon{\vec\epsilon}$
$\newcommand\Vvarepsilon{\vec\varepsilon}$
$\newcommand\Vzeta{\vec\zeta}$
$\newcommand\Veta{\vec\eta}$
$\newcommand\Vtheta{\vec\theta}$
$\newcommand\Vvartheta{\vec\vartheta}$
$\newcommand\Viota{\vec\iota}$
$\newcommand\Vkappa{\vec\kappa}$
$\newcommand\Vlambda{\vec\lambda}$
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\VTheta{\vec\Theta}$
$\newcommand\VLambda{\vec\Lambda}$
$\newcommand\VXi{\vec\Xi}$
$\newcommand\VPi{\vec\Pi}$
$\newcommand\VSigma{\vec\Sigma}$
$\newcommand\VUps{\vec\Upsilon}$
$\newcommand\VPhi{\vec\Phi}$
$\newcommand\VPsi{\vec\Psi}$
$\newcommand\VOmega{\vec\Omega}$
$\newcommand\BA{\mib A}$
$\newcommand\BB{\mib B}$
$\newcommand\BC{\mib C}$
$\newcommand\BD{\mib D}$
$\newcommand\BE{\mib E}$
$\newcommand\BF{\mib F}$
$\newcommand\BG{\mib G}$
$\newcommand\BH{\mib H}$
$\newcommand\BI{\mib I}}$
$\newcommand\BJ{\mib J}$
$\newcommand\BK{\mib K}$
$\newcommand\BL{\mib L}$
$\newcommand\BM{\mib M}$
$\newcommand\BN{\mib N}$
$\newcommand\BO{\mib O}$
$\newcommand\BP{\mib P}$
$\newcommand\BQ{\mib Q}$
$\newcommand\BR{\mib R}$
$\newcommand\BS{\mib S}$
$\newcommand\BT{\mib T}$
$\newcommand\BU{\mib U}$
$\newcommand\BV{\mib V}$
$\newcommand\BW{\mib W}$
$\newcommand\BX{\mib X}$
$\newcommand\BY{\mib Y}$
$\newcommand\BZ{\mib Z}$
$\newcommand\Ba{\mib a}$
$\newcommand\Bb{\mib b}$
$\newcommand\Bc{\mib c}$
$\newcommand\Bd{\mib d}$
$\newcommand\Be{\mib e}$
$\newcommand\Bf{\mib f}$
$\newcommand\Bg{\mib g}$
$\newcommand\Bh{\mib h}$
$\newcommand\Bi{\mib i}$
$\newcommand\Bj{\mib j}$
$\newcommand\Bk{\mib k}$
$\newcommand\Bl{\mib l}$
$\newcommand\Bm{\mib m}$
$\newcommand\Bn{\mib n}$
$\newcommand\Bo{\mib o}$
$\newcommand\Bp{\mib p}$
$\newcommand\Bq{\mib q}$
$\newcommand\Br{\mib r}$
$\newcommand\Bs{\mib s}$
$\newcommand\Bt{\mib t}$
$\newcommand\Bu{\mib u}$
$\newcommand\Bv{\mib v}$
$\newcommand\Bw{\mib w}$
$\newcommand\Bx{\mib x}$
$\newcommand\By{\mib y}$
$\newcommand\Bz{\mib z}$\)
$\newcommand\vrh{\varrho}$
$\newcommand\vsig{\varsigma}$
$\newcommand\ups{\upsilon}$
$\newcommand\eps{\epsilon}$
$\newcommand\ve{\varepsilon}$
$\newcommand\vth{\vartheta}$
$\newcommand\vphi{\varphi}$
$\newcommand\xhi{\chi}$
$\newcommand\Ups{\Upsilon}$
$\newcommand\Balpha{\mib\alpha}$
$\newcommand\Bbeta{\mib\beta}$
$\newcommand\Bgamma{\mib\gamma}$
$\newcommand\Bdelta{\mib\delta}$
$\newcommand\Beps{\mib\epsilon}$
$\newcommand\Bve{\mib\varepsilon}$
$\newcommand\Bzeta{\mib\zeta}$
$\newcommand\Beta{\mib\eta}$
$\newcommand\Btheta{\mib\theta}$
$\newcommand\Bvth{\mib\vartheta}$
$\newcommand\Biota{\mib\iota}$
$\newcommand\Bkappa{\mib\kappa}$
$\newcommand\Blambda{\mib\lambda}$
$\newcommand\Bmu{\mib\mu}$
$\newcommand\Bnu{\mib\nu}$
$\newcommand\Bxi{\mib\xi}$
$\newcommand\Bom{\mib\omicron}$
$\newcommand\Bpi{\mib\pi}$
$\newcommand\Bvarpi{\mib\varpi}$
$\newcommand\Brho{\mib\rho}$
$\newcommand\Bvrh{\mib\varrho}$
$\newcommand\Bsigma{\mib\sigma}$
$\newcommand\Bvsig{\mib\varsigma}$
$\newcommand\Btau{\mib\tau}$
$\newcommand\Bups{\mib\upsilon}$
$\newcommand\Bphi{\mib\phi}$
$\newcommand\Bvphi{\mib\vphi}$
$\newcommand\Bchi{\mib\chi}$
$\newcommand\Bpsi{\mib\psi}$
$\newcommand\Bomega{\mib\omega}$
$\newcommand\BGamma{\mib\Gamma}$
$\newcommand\BDelta{\mib\Delta}$
$\newcommand\BTheta{\mib\Theta}$
$\newcommand\BLambda{\mib\Lambda}$
$\newcommand\BXi{\mib\Xi}$
$\newcommand\BPi{\mib\Pi}$
$\newcommand\BSigma{\mib\Sigma}$
$\newcommand\BUps{\mib\Upsilon}$
$\newcommand\BPhi{\mib\Phi}$
$\newcommand\BPsi{\mib\Psi}$
$\newcommand\BOmega{\mib\Omega}$
$\newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}$
$\newcommand\RGamma{ \Gamma}$
$\newcommand\RDelta{ \Delta}$
$\newcommand\RTheta{ \Theta}$
$\newcommand\RLambda{ \Lambda}$
$\newcommand\RXi{ \Xi}$
$\newcommand\RPi{ \Pi}$
$\newcommand\RSigma{ \Sigma}$
$\newcommand\RUps{ \Upsilon}$
$\newcommand\RPhi{ \Phi}$
$\newcommand\RPsi{ \Psi}$
$\newcommand\ROmega{ \Omega}$
$\newcommand\RA{ A}$
$\newcommand\RB{ B}$
$\newcommand\RC{ C}$
$\newcommand\RD{ D}$
$\newcommand\RE{ E}$
$\newcommand\RF{ F}$
$\newcommand\RG{ G}$
$\newcommand\RH{ H}$
$\newcommand\RI{ I}$
$\newcommand\RJ{ J}$
$\newcommand\RK{ K}$
$\newcommand\RL{ L}$
$\newcommand { M}$
$\newcommand\RN{ N}$
$\newcommand\RO{ O}$
$\newcommand\RP{ P}$
$\newcommand\RQ{ Q}$
$\newcommand\RR{ R}$
$\newcommand\RS{ S}$
$\newcommand\RT{ T}$
$\newcommand\RU{ U}$
$\newcommand\RV{ V}$
$\newcommand\RW{ W}$
$\newcommand\RX{ X}$
$\newcommand\RY{ Y}$
$\newcommand\RZ{ Z}$
$\newcommand\Ra{ a}$
$\newcommand\Rb{ b}$
$\newcommand\Rc{ c}$
$\newcommand\Rd{ d}$
$\newcommand\Re{ e}$
$\newcommand\Rf{ f}$
$\newcommand\Rg{ g}$
$\newcommand\Rh{ h}$
$\newcommand\Ri{ i}$
$\newcommand\Rj{ j}$
$\newcommand\Rk{ k}$
$\newcommand\Rl{ l}$
$\newcommand { m}$
$\newcommand\Rn{ n}$
$\newcommand\Ro{ o}$
$\newcommand\Rp{ p}$
$\newcommand\Rq{ q}$
$\newcommand\Rr{ r}$
$\newcommand\Rs{ s}$
$\newcommand\Rt{ t}$
$\newcommand\Ru{ u}$
$\newcommand\Rv{ v}$
$\newcommand\Rw{ w}$
$\newcommand\Rx{ x}$
$\newcommand\Ry{ y}$
$\newcommand\Rz{ z}$
$\newcommand\BBA{\boldsymbol\RA}$
$\newcommand\BBB{\boldsymbol\RB}$
$\newcommand\BBC{\boldsymbol\RC}$
$\newcommand\BBD{\boldsymbol\RD}$
$\newcommand\BBE{\boldsymbol\RE}$
$\newcommand\BBF{\boldsymbol\RF}$
$\newcommand\BBG{\boldsymbol\RG}$
$\newcommand\BBH{\boldsymbol\RH}$
$\newcommand\BBI{\boldsymbol\RI}$
$\newcommand\BBJ{\boldsymbol\RJ}$
$\newcommand\BBK{\boldsymbol\RK}$
$\newcommand\BBL{\boldsymbol\RL}$
$\newcommand\BBM{\boldsymbol }$
$\newcommand\BBN{\boldsymbol\RN}$
$\newcommand\BBO{\boldsymbol\RO}$
$\newcommand\BBP{\boldsymbol\RP}$
$\newcommand\BBQ{\boldsymbol\RQ}$
$\newcommand\BBR{\boldsymbol\RR}$
$\newcommand\BBS{\boldsymbol\RS}$
$\newcommand\BBT{\boldsymbol\RT}$
$\newcommand\BBU{\boldsymbol\RU}$
$\newcommand\BBV{\boldsymbol\RV}$
$\newcommand\BBW{\boldsymbol\RW}$
$\newcommand\BBX{\boldsymbol\RX}$
$\newcommand\BBY{\boldsymbol\RY}$
$\newcommand\BBZ{\boldsymbol\RZ}$
$\newcommand\BBa{\boldsymbol\Ra}$
$\newcommand\BBb{\boldsymbol\Rb}$
$\newcommand\BBc{\boldsymbol\Rc}$
$\newcommand\BBd{\boldsymbol\Rd}$
$\newcommand\BBe{\boldsymbol\Re}$
$\newcommand\BBf{\boldsymbol\Rf}$
$\newcommand\BBg{\boldsymbol\Rg}$
$\newcommand\BBh{\boldsymbol\Rh}\}$
$\newcommand\BBi{\boldsymbol\Ri}$
$\newcommand\BBj{\boldsymbol\Rj}$
$\newcommand\BBk{\boldsymbol\Rk}$
$\newcommand\BBl{boldsymbol\Rl}$
$\newcommand\BBm{\boldsymbol }$
$\newcommand\BBn{\boldsymbol\Rn}$
$\newcommand\BBo{\boldsymbol\Ro}$
$\newcommand\BBp{\boldsymbol\Rp}$
$\newcommand\BBq{\boldsymbol\Rq}$
$\newcommand\BBr{\boldsymbol\Rr}$
$\newcommand\BBs{\boldsymbol\Rs}$
$\newcommand\BBt{\boldsymbol\Rt}$
$\newcommand\BBu{\boldsymbol\Ru}$
$\newcommand\BBv{\boldsymbol\Rv}$
$\newcommand\BBw{\boldsymbol\Rw}$
$\newcommand\BBx{\boldsymbol\Rx}$
$\newcommand\BBy{\boldsymbol\Ry}$
$\newcommand\BBz{\boldsymbol\Rz}$
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
$\newcommand\bnabla{\boldsymbol{\nabla}}$
$\newcommand\Bell{\boldsymbol\ell}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\newcommand\ns{^\vphantom{*}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}$
$\newcommand\izpi{\int\limits_{0}^{\infty}\!\!}$
$\newcommand\etc{\it etc.\/}$
$\newcommand\etal{\it et al.\/}$
$\newcommand\opcit{\it op. cit.\/}$
$\newcommand\ie{\it i.e.\/}$
$\newcommand\Ie{\it I.e.\/}$
$\newcommand\viz{\it viz.\/}$
$\newcommand\eg{\it e.g.\/}$
$\newcommand\Eg{\it E.g.\/}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\def\sss#1{\scriptscriptstyle #1}$
$\def\ss#1{\scriptstyle #1}$
$\def\ssr#1{\scriptstyle #1}$
$\def\ssf#1{\scriptstyle #1}$
$\newcommand\NA{N_{\ssr{\!A}}}$
$\newcommand\lala{\langle\!\langle}$
$\newcommand\rara{\rangle\!\rangle}$
$\newcommand\blan{\big\langle}$
$\newcommand\bran{\big\rangle}$
$\newcommand\Blan{\Big\langle}$
$\newcommand\Bran{\Big\rangle}$
$\newcommand\intl{\int\limits}$
$\newcommand\half{\frac{1}{2}}$
$\newcommand\third{\frac{1}{3}}$
$\newcommand\fourth{\frac{1}{4}}$
$\newcommand\eighth{\frac{1}{8}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\undertext#1{$\underline{\hbox{#1}}$}$
$\newcommand\Tra{\mathop{\textsf{Tr}}\,}$
$\newcommand\det{\mathop{\textsf{det}}\,}$
$\def\tket#1{|  #1 \rangle}$
$\def\tbra#1{\langle #1|}$
$\def\tbraket#1#2{\langle #1  |   #2 \rangle}$
$\def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}$
$\def\sket#1{|  \, #1 \,  \rangle}$
$\def\sbra#1{\langle \,  #1 \, |}$
$\def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}$
$\def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}$
$\def\ket#1{\big| \, #1\, \big\rangle}$
$\def\bra#1{\big\langle \, #1 \, \big|}$
$\def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}$
$\def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}$
$\newcommand\pz{\partial}$
$\newcommand\pzb{\bar{\partial}}$
$\newcommand\svph{\vphantom{\int}}$
$\newcommand\vph{\vphantom{\sum_i}}$
$\newcommand\bvph{\vphantom{\sum_N^N}}$
$\newcommand\nd{^{\vphantom{\dagger}}}$
$\newcommand\ns{^{\vphantom{*}}}$
$\newcommand\yd{^\dagger}$
$\newcommand\zb{\bar z}$
$\newcommand\zdot{\dot z}$
$\newcommand\zbdot{\dot{\bar z}}$
$\newcommand\kB{k_{\sss{B}}}$
$\newcommand\kT{k_{\sss{B}}T}$
$\newcommand\gtau{g_\tau}$
$\newcommand\Htil{\tilde H}$
$\newcommand\pairo{(\phi\nd_0,J\nd_0)}$
$\newcommand\pairm{(\phi\nd_0,J)}$
$\newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}$
$\newcommand\pairmb{(\Bphi\nd_0,\BJ)}$
$\newcommand\pair{(\phi,J)}$
$\newcommand\Hz{H\nd_0}$
$\newcommand\Ho{H\nd_1}$
$\newcommand\Htz{\Htil\nd_0}$
$\newcommand\Hto{\Htil\nd_1}$
$\newcommand\oc{\omega_\Rc}$

$\newcommand \gtwid{\approx}$

$\newcommand\index{\textsf{ind}}$
$\newcommand\csch{\,{ csch\,}}$
$\newcommand\ctnh{\,{ ctnh\,}}$
$\newcommand\ctn{\,{ ctn\,}}$
$\newcommand\sgn{\,{ sgn\,}}$
$\def\tmapright#1{\xrightarrow \limits^{#1}}$
$\def\bmapright#1{\xrightarrow\limits_{#1}}$
$\newcommand\hfb{\hfill\break}$
$\newcommand\Rep{\textsf{Re}\,}$
$\newcommand\Imp{\textsf{Im}\,}$
$\newcommand\ncdot{\!\cdot\!}$
$\def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }$
$\def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }$
$\newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}$

$\def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}$
$\def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}$
$\def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}$
$\def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}$
$\newcommand\subA{\ns_\ssr{A}}$
$\newcommand\subB{\ns_\ssr{B}}$
$\newcommand\subC{\ns_\ssr{C}}$
$\newcommand\subD{\ns_\ssr{D}}$
$\newcommand\subAB{\ns_\ssr{AB}}$
$\newcommand\subBC{\ns_\ssr{BC}}$
$\newcommand\subCD{\ns_\ssr{CD}}$
$\newcommand\subDA{\ns_\ssr{DA}}$
$\def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }$
$\def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}$
$\newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}$
$\newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}$
$\newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}$
$\newcommand\cds{\,\bullet\,}$
$\newcommand\ccs{\,\circ\,}$
$\newcommand\nsub{_{\vphantom{\dagger}}}$
$\newcommand\rhohat{\hat\rho}$
$\newcommand\vrhhat{\hat\vrh}$
$\newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}$
$\newcommand\brangle{\big\rangle}$
$\newcommand\blangle{\big\langle}$
$\newcommand\vet{\tilde\ve}$
$\newcommand\zbar{\bar z}$
$\newcommand\ftil{\tilde f}$
$\newcommand\XBE{\RXi\ns_\ssr{BE}}$
$\newcommand\XFD{\RXi\ns_\ssr{FD}}$
$\newcommand\OBE{\Omega\ns_\ssr{BE}}$
$\newcommand\OFD{\Omega\ns_\ssr{FD}}$
$\newcommand\veF{\ve\ns_\RF}$
$\newcommand\kF{k\ns_\RF}$
$\newcommand\kFu{k\ns_{\RF\uar}}$
$\newcommand\SZ{\textsf Z}}$ \( \newcommand\kFd{k\ns_{\RF\dar}\)
$\newcommand\muB{\mu\ns_\ssr{B}}$
$\newcommand\mutB{\tilde\mu}\ns_\ssr{B}$
$\newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}$
$\newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}$
$\newcommand\xhiOZ{\xhi^\ssr{OZ}}$
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\jhz{\HJ(0)}$
$\newcommand\nda{\nd_\alpha}$
$\newcommand\ndap{\nd_{\alpha'}}$
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.01:_What_is_Thermodynamics), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\msa{m\ns_\ssr{A}}$
$\newcommand\msb{m\ns_\ssr{B}}$
$\newcommand\mss{m\ns_\Rs}$
$\newcommand\HBx{\hat\Bx}$
$\newcommand\HBy{\hat\By}$
$\newcommand\HBz{\hat\Bz}$
$\newcommand\thm{\theta\ns_m}$
$\newcommand\thp{\theta\ns_\phi}$
$\newcommand\mtil{\widetilde m}$
$\newcommand\phitil{\widetilde\phi}$
$\newcommand\delf{\delta\! f}$
$\newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}$
$\newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}$
$\newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}$
$\newcommand\vbar{\bar v}$
$\newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}$
$\newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}$
$\newcommand\gla{g\nd_{\RLambda\nd}}$
$\newcommand\TA{T\ns_\ssr{A}}$
$\newcommand\TB{T\ns_\ssr{B}}$
$\newcommand\ncdot{\!\cdot\!}$
$\newcommand\NS{N\ns_{\textsf S}}$

Thermodynamics is the study of relations among the state variables describing a thermodynamic system, and of transformations of heat into work and vice versa.

Thermodynamic systems and state variables

Thermodynamic systems contain large numbers of constituent particles, and are described by a set of state variables which describe the system’s properties in an average sense. State variables are classified as being either extensive or intensive.

Extensive variables, such as volume $V$, particle number $N$, total internal energy $E$, magnetization $M$, , scale linearly with the system size, as the first power of the system volume. If we take two identical thermodynamic systems, place them next to each other, and remove any barriers between them, then all the extensive variables will double in size.

Intensive variables, such as the pressure $p$, the temperature $T$, the chemical potential $\mu$, the electric field $\BE$, , are independent of system size, scaling as the zeroth power of the volume. They are the same throughout the system, if that system is in an appropriate state of equilibrium. The ratio of any two extensive variables is an intensive variable. For example, we write $n=N/V$ for the number density, which scales as $V^0$. Intensive variables may also be inhomogeneous. For example, $n(\Br)$ is the number density at position $\Br$, and is defined as the limit of $\RDelta N/\RDelta V$ of the number of particles $\RDelta N$ inside a volume $\RDelta V$ which contains the point $\Br$, in the limit $V \gg \RDelta V \gg V/N$.

Classically, the full motion of a system of $N$ point particles requires $6N$ variables to fully describe it ($3N$ positions and $3N$ velocities or momenta, in three space dimensions)¹. Since the constituents are very small, $N$ is typically very large. A typical solid or liquid, for example, has a mass density on the order of $\vrh\sim 1\,\Rg/{cm}^3$; for gases, $\vrh\sim 10^{-3}\,\Rg/{cm}^3$. The constituent atoms have masses of $10^0$ to $10^2$ grams per mole, where one mole of $X$ contains $\NA$ of $X$, and $\NA=6.0221415\times 10^{23}$ is Avogadro’s number². Thus, for solids and liquids we roughly expect number densities $n$ of $10^{-2} - 10^{0}\,{mol}/{cm}^3$ for solids and liquids, and $10^{-5} - 10^{-3}\,{mol}/{cm}^3$ for gases. Clearly we are dealing with fantastically large numbers of constituent particles in a typical thermodynamic system. The underlying theoretical basis for thermodynamics, where we use a small number of state variables to describe a system, is provided by the microscopic theory of statistical mechanics, which we shall study in the weeks ahead.

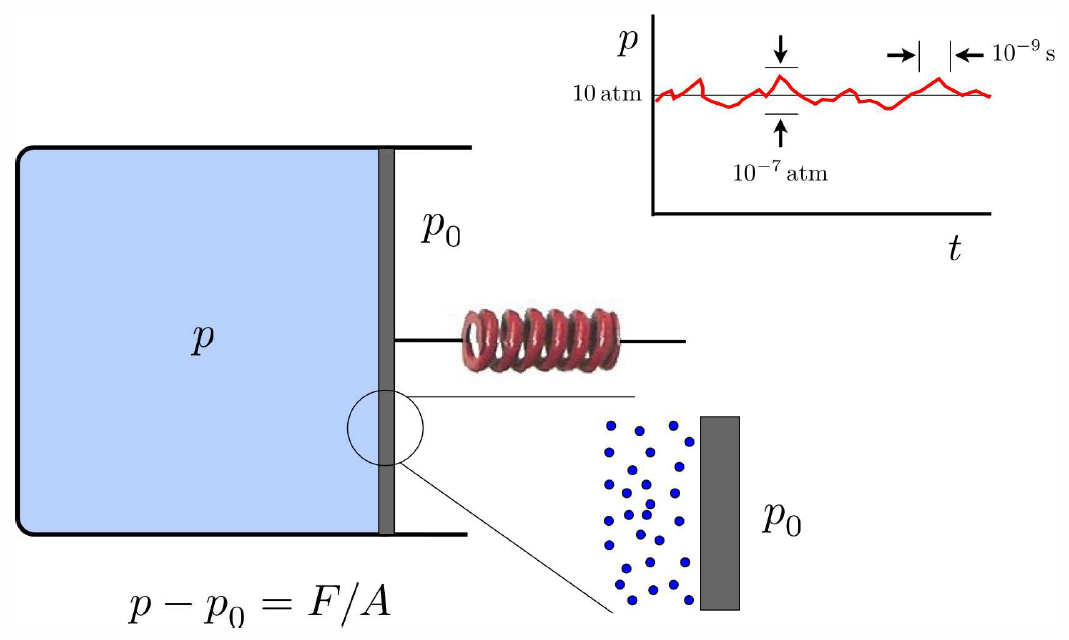
Intensive quantities such as $p$, $T$, and $n$ ultimately involve averages over both space and time. Consider for example the case of a gas enclosed in a container. We can measure the pressure (relative to atmospheric pressure) by attaching a spring to a moveable wall, as shown in Fig. [pressure]. From the displacement of the spring and the value of its spring constant $k$ we determine the force $F$. This force is due to the difference in pressures, so $p=p\ns_0+F/A$. Microscopically, the gas consists of constituent atoms or molecules, which are constantly undergoing collisions with each other and with the walls of the container. When a particle bounces off a wall, it imparts an impulse $2\nhat (\nhat\cdot\Bp)$, where $\Bp$ is the particle’s momentum and $\nhat$ is the unit vector normal to the wall. (Only particles with $\Bp\cdot\nhat>0$ will hit the wall.) Multiply this by the number of particles colliding with the wall per unit time, and one finds the net force on the wall; dividing by the area gives the pressure $p$. Within the gas, each particle travels for a distance $\ell$, called the mean free path, before it undergoes a collision. We can write $\ell={\bar v}\tau$, where ${\bar v}$ is the average particle speed and $\tau$ is the mean free time. When we study the kinetic theory of gases, we will derive formulas for $\ell$ and ${\bar v}$ (and hence $\tau$). For now it is helpful to quote some numbers to get an idea of the relevant distance and time scales. For $\RO\ns_2$ gas at standard temperature and pressure ($T=0^\circ\,$C, $p=1\,$atm), the mean free path is $\ell\approx 1.1\times 10^{-5}$ cm, the average speed is ${\bar v}\approx 480\, \Rm/\Rs$, and the mean free time is $\tau\approx 2.5\times 10^{-10}\,$s. Thus, particles in the gas undergo collisions at a rate $\tau^{-1}\approx 4.0\times 10^9\,\Rs^{-1}$. A measuring device, such as our spring, or a thermometer, effectively performs time and space averages. If there are $N\ns_\Rc$ collisions with a particular patch of wall during some time interval on which our measurement device responds, then the root mean square relative fluctuations in the local pressure will be on the order of $N_\Rc^{-1/2}$ times the average. Since $N\ns_\Rc$ is a very large number, the fluctuations are negligible.

[politics] From microscale to macroscale : physical versus social sciences.

If the system is in steady state, the state variables do not change with time. If furthermore there are no macroscopic currents of energy or particle number flowing through the system, the system is said to be in equilibrium. A continuous succession of equilibrium states is known as a thermodynamic path, which can be represented as a smooth curve in a multidimensional space whose axes are labeled by state variables. A thermodynamic process is any change or succession of changes which results in a change of the state variables. In a cyclic process, the initial and final states are the same. In a quasistatic process, the system passes through a continuous succession of equilibria. A reversible process is one where the external conditions and the thermodynamic path of the system can be reversed; it is both quasi-static and non-dissipative ( no friction). The slow expansion of a gas against a piston head, whose counter-force is always infinitesimally less than the force $pA$ exerted by the gas, is reversible. To reverse this process, we simply add infinitesimally more force to $pA$ and the gas compresses. An example of a quasistatic process which is not reversible: slowly dragging a block across the floor, or the slow leak of air from a tire. Irreversible processes, as a rule, are dissipative. Other special processes include isothermal ($dT=0$), isobaric ($dp=0$), isochoric ($dV=0$), and adiabatic ($\dbar Q=0$, no heat exchange): $$\begin{aligned} \hbox{\sl reversible:}\ &\dbar Q = T\,dS & \hbox{\sl isothermal:}\ dT&=0 \\ \hbox{\sl spontaneous:}\ &\dbar Q < T\,dS & \hbox{\sl isochoric:}\ dV&=0 \\ \hbox{\sl adiabatic:}\ &\dbar Q =0 & \hbox{\sl isobaric:}\ dp&=0\quad.\end{aligned}$$ We shall discuss later the entropy $S$ and its connection with irreversibility.

[pressure] The pressure $p$ of a gas is due to an average over space and time of the impulses due to the constituent particles.

How many state variables are necessary to fully specify the equilibrium state of a thermodynamic system? For a single component system, such as water which is composed of one constituent molecule, the answer is three. These can be taken to be $T$, $p$, and $V$. One always must specify at least one extensive variable, else we cannot determine the overall size of the system. For a multicomponent system with $g$ different species, we must specify $g+2$ state variables, which may be $\{T,p,N\ns_1,\ldots,N\ns_g\}$, where $N\ns_a$ is the number of particles of species $a$. Another possibility is the set $(T,p,V, x\ns_1,\ldots,x\ns_{g-1}\}$, where the concentration of species $a$ is $x\ns_a=N\ns_a/N$. Here, $N=\sum_{a=1}^g N\ns_a$ is the total number of particles. Note that $\sum_{a=1}^g x\ns_a=1$.

If then follows that if we specify more than $g+2$ state variables, there must exist a relation among them. Such relations are known as equations of state. The most famous example is the ideal gas law, $$pV=N\kT\ ,$$ relating the four state variables $T$, $p$, $V$, and $N$. Here $\kB=1.3806503\times 10^{-16}\,{erg}/\RK$ is Boltzmann’s constant. Another example is the van der Waals equation, $$\bigg(p+{aN^2\over V^2}\bigg) (V-bN) = N\kT\ ,$$ where $a$ and $b$ are constants which depend on the molecule which forms the gas. For a third example, consider a paramagnet, where $${M\over V}={CH\over T}\ ,$$ where $M$ is the magnetization, $H$ the magnetic field, and $C$ the Curie constant.

Any quantity which, in equilibrium, depends only on the state variables is called a state function. For example, the total internal energy $E$ of a thermodynamics system is a state function, and we may write $E=E(T,p,V)$. State functions can also serve as state variables, although the most natural state variables are those which can be directly measured.

Heat

Once thought to be a type of fluid, heat is now understood in terms of the kinetic theory of gases, liquids, and solids as a form of energy stored in the disordered motion of constituent particles. The units of heat are therefore units of energy, and it is appropriate to speak of heat energy, which we shall simply abbreviate as heat:³ $$1\,\RJ = 10^7\,{erg} = 6.242\times 10^{18}\,{eV}= 2.390\times 10^{-4}\,{kcal} = 9.478\times 10^{-4}\,{BTU}\ .$$ We will use the symbol $Q$ to denote the amount of heat energy absorbed by a system during some given thermodynamic process, and $\dbar Q$ to denote a differential amount of heat energy. The symbol $\dbar$ indicates an ‘inexact differential’, about which we shall have more to say presently. This means that heat is not a state function: there is no ‘heat function’ $Q(T,p,V)$.

Work

In general we will write the differential element of work $\dbar W$ done by the system as $$\dbar W=\sum_i F\ns_i\,dX\ns_i\ ,$$ where $F\ns_i$ is a generalized force and $dX\ns_i$ a generalized displacement⁴. The generalized forces and displacements are themselves state variables, and by convention we will take the generalized forces to be intensive and the generalized displacements to be extensive. As an example, in a simple one-component system, we have $\dbar W=p\,dV$. More generally, we write $$\qquad\dbar W =\ \stackrel{-\sum_j y\ns_j \, dX\ns_j}{\overbrace{\big(p\,dV- \BH\cdot d\BM - \BE\cdot d\BP - \sigma\,dA + \ldots \big)}} -\stackrel{\sum_a \mu\ns_a\, dN\ns_a}{\overbrace{\big(\mu\ns_1 \,dN\ns_1 + \mu\ns_2\,d N\ns_2 + \ldots\big) }} \label{dwork}$$ Here we distinguish between two types of work. The first involves changes in quantities such as volume, magnetization, electric polarization, area, The conjugate forces $y\ns_i$ applied to the system are then $-p$, the magnetic field $\BH$, the electric field $\BE$, the surface tension $\sigma$, respectively. The second type of work involves changes in the number of constituents of a given species. For example, energy is required in order to dissociate two hydrogen atoms in an $\RH\ns_2$ molecule. The effect of such a process is $dN\ns_{\RH\ns_2}=-1$ and $dN\ns_\RH=+2$.

As with heat, $\dbar W$ is an inexact differential, and work $W$ is not a state variable, since it is path-dependent. There is no ‘work function’ $W(T,p,V)$.

Pressure and Temperature

The units of pressure ($p$) are force per unit area. The SI unit is the Pascal (Pa): $1\,{Pa}=1\,\RN/\Rm^2=1\,{kg}/\Rm\,\Rs^2$. Other units of pressure we will encounter: $$\begin{aligned} 1\,{bar}&\equiv 10^5\,{Pa}\\ 1\,{atm}&\equiv 1.01325\times 10^5\,{Pa}\\ 1\,{torr}&\equiv 133.3\,{Pa}\ .\end{aligned}$$

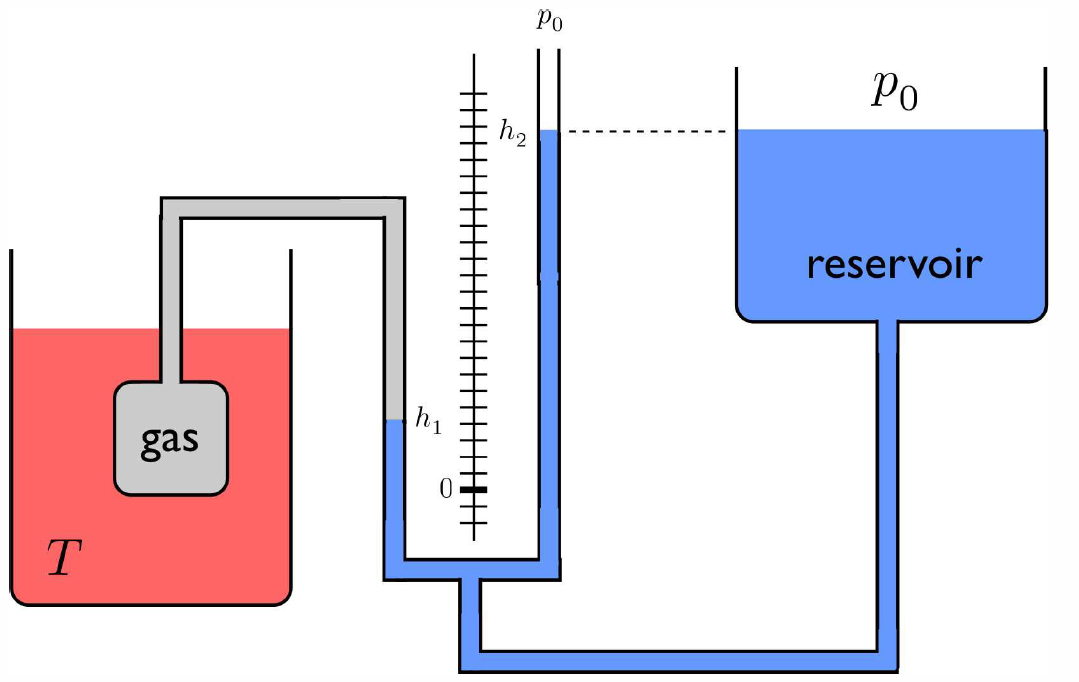
Temperature ($T$) has a very precise definition from the point of view of statistical mechanics, as we shall see. Many physical properties depend on the temperature – such properties are called thermometric properties. For example, the resistivity of a metal $\rho(T,p)$ or the number density of a gas $n(T,p)$ are both thermometric properties, and can be used to define a temperature scale. Consider the device known as the ‘constant volume gas thermometer’ depicted in Fig. [CVGTa], in which the volume or pressure of a gas may be used to measure temperature. The gas is assumed to be in equilibrium at some pressure $p$, volume $V$, and temperature $T$. An incompressible fluid of density $\vrh$ is used to measure the pressure difference $\RDelta p = p-p\ns_0$, where $p\ns_0$ is the ambient pressure at the top of the reservoir: $$p-p\ns_0=\vrh g (h\ns_2-h\ns_1)\ ,$$ where $g$ is the acceleration due to gravity. The height $h\ns_1$ of the left column of fluid in the U-tube provides a measure of the change in the volume of the gas: $$V(h\ns_1)=V(0)-A h\ns_1\ ,$$ where $A$ is the (assumed constant) cross-sectional area of the left arm of the U-tube. The device can operate in two modes:

• Constant pressure mode : The height of the reservoir is adjusted so that the height difference $h\ns_2-h\ns_1$ is held constant. This fixes the pressure $p$ of the gas. The gas volume still varies with temperature $T$, and we can define $${T\over T\ns_{ref}} = {V\over V\ns_{ref}}\ ,$$ where $T\ns_{ref}$ and $V\ns_{ref}$ are the reference temperature and volume, respectively.
• Constant volume mode : The height of the reservoir is adjusted so that $h\ns_1=0$, hence the volume of the gas is held fixed, and the pressure varies with temperature. We then define $${T\over T\ns_{ref}} = {p\over p\ns_{ref}}\ ,$$ where $T\ns_{ref}$ and $p\ns_{ref}$ are the reference temperature and pressure, respectively.

[CVGTa] The constant volume gas thermometer. The gas is placed in thermal contact with an object of temperature $T$. An incompressible fluid of density $\vrh$ is used to measure the pressure difference $\RDelta p = p_{gas} - p_0$.

What should we use for a reference? One might think that a pot of boiling water will do, but anyone who has gone camping in the mountains knows that water boils at lower temperatures at high altitude (lower pressure). This phenomenon is reflected in the phase diagram for $\RH\ns_2\RO$, depicted in Fig. [H2Opd]. There are two special points in the phase diagram, however. One is the triple point, where the solid, liquid, and vapor (gas) phases all coexist. The second is the critical point, which is the terminus of the curve separating liquid from gas. At the critical point, the latent heat of transition between liquid and gas phases vanishes (more on this later on). The triple point temperature $T\ns_\Rt$ at thus unique and is by definition $T\ns_\Rt=273.16\,$K. The pressure at the triple point is $611.7\,{Pa}=6.056\times 10^{-3}\,{atm}$.

[H2Opd] A sketch of the phase diagram of $\RH_2\RO$ (water). Two special points are identified: the triple point $(T_\Rt,p_\Rt)$ at which there is three phase coexistence, and the critical point $(T_\Rc,p_\Rc)$, where the latent heat of transformation from liquid to gas vanishes. Not shown are transitions between several different solid phases.

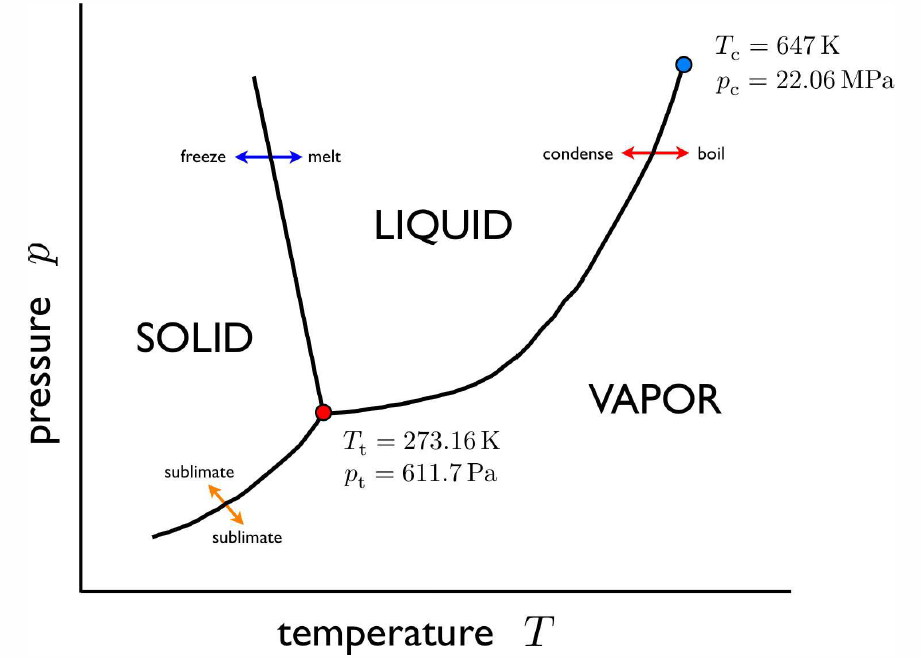
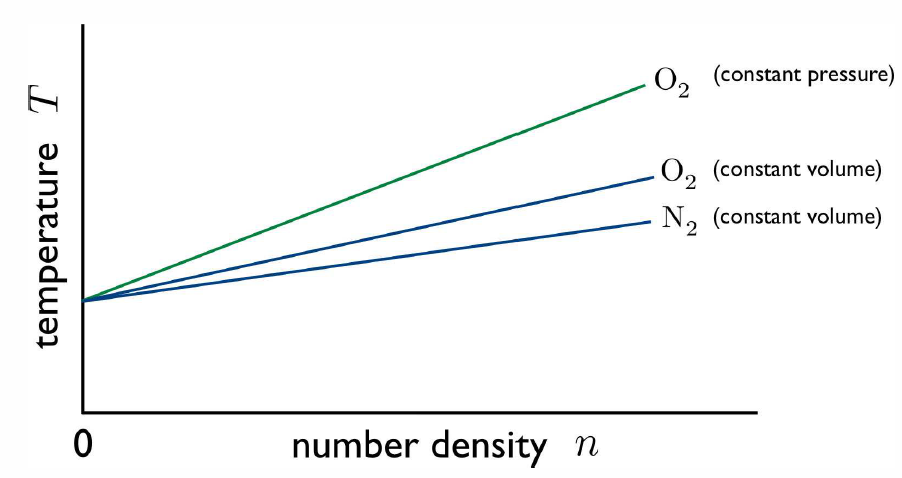
A question remains: are the two modes of the thermometer compatible? it we boil water at $p=p\ns_0=1\,$atm, do they yield the same value for $T$? And what if we use a different gas in our measurements? In fact, all these measurements will in general be incompatible, yielding different results for the temperature $T$. However, in the limit that we use a very low density gas, all the results converge. This is because all low density gases behave as ideal gases, and obey the ideal gas equation of state $pV=N\kT$.

Standard temperature and pressure

It is customary in the physical sciences to define certain standard conditions with respect to which any arbitrary conditions may be compared. In thermodynamics, there is a notion of standard temperature and pressure, abbreviated STP. Unfortunately, there are two different definitions of STP currently in use, one from the International Union of Pure and Applied Chemistry (IUPAC), and the other from the U.S. National Institute of Standards and Technology (NIST). The two standards are: $$\begin{aligned} {IUPAC}\ &:\ T\ns_0=0^\circ\,\RC=273.15\,\RK\quad\ \ ,\quad p\ns_0=10^5\,{Pa}\\ {NIST}\ &:\ T\ns_0=20^\circ\,\RC=293.15\,\RK\quad,\quad p\ns_0=1\,{atm}=1.01325\times 10^5\,{Pa}\end{aligned}$$ To make matters worse, in the past it was customary to define STP as $T\ns_0=0^\circ\,\RC$ and $p\ns_0=1\,$atm. We will use the NIST definition in this course. Unless I slip and use the IUPAC definition. Figuring out what I mean by STP will keep you on your toes.

The volume of one mole of ideal gas at STP is then $$V={\NA\kB T\ns_0\over p\ns_0}=\begin{cases} 22.711 \> \ell& {(IUPAC)} \\ 24.219 \> \ell & {(NIST)}\ , \end{cases}$$ where $1\,\ell=10^6\,{cm}^3=10^{-3}\,\Rm^3$ is one liter. Under the old definition of STP as $T\ns_0=0^\circ\,\RC$ and $p\ns_0=1\,$atm, the volume of one mole of gas at STP is $22.414\>\ell$, which is a figure I remember from my $10^{th}$ grade chemistry class with Mr. Lawrence.

[CVGTb] As the gas density tends to zero, the readings of the constant volume gas thermometer converge.