11.E: Lorentz Transformations (Exercises)

11.1

Suppose system \(S^\prime\) moves with respect to \(S\) with velocity \(u\), and \(S^{\prime\prime}\) moves with respect to \(S^\prime\) with velocity \(v\). Show that system \(S^{\prime\prime}\) and \(S\) are related through a Lorentz transformation with velocity

\[w=\frac{u+v}{1+\frac{uv}{c^2}}.\]

11.2

Equation (11.13) gives the Lorentz transformation for an observer moving in an arbitrary direction \(\textbf{u}\).

(a) Show that if a ray of light is emitted in the rest frame \(S\) in an arbitrary direction, such that its trajectory is described by \(\textbf{x}=\textbf{c}t\) (where \(\textbf{c}\cdot\textbf{c}=c^2\)), then in the moving frame \(S^\prime\), the trajectory of the ray of light is also a straight line, given by \(\textbf{x}^\prime=\textbf{c}^\prime t^\prime\), with \(\textbf{c}^\prime\cdot\textbf{c}^\prime=c^2\).

(b) What is the direction of the ray of light in \(S^\prime\)?

11.3

(a) A male and a female student both attend lectures on relativity. Afterwards, they return home by train, moving in opposite directions, each at \((4/5)c\). Before they left, they promised to send each other messages while on the train. Unfortunately there is interference in the phone network, so they can’t use their phones to do so. They do have pen and paper though, so they could write down their message and throw it to the other train. The boy, having only paid attention during the first part of the lecture (being distracted by the girl afterwards) remembers that nothing can go faster than the speed of light, and concludes that throwing something is pointless, as the (classical) relative speed of the trains exceeds the speed of light. The girl, who paid attention throughout, realizes this is not the case, and explains why in her note to the boy. At which minimum velocity should she throw the note so that it can reach the boy’s train?

(b) The boy, having received the girl’s message, realizes that he has a much better chance of completing the assignments if he can ask her some more questions. He therefore leaves his train, and takes the next one back (so now traveling in the same direction as the girl). Unfortunately, this train only moves at \((3/5)c\), so it won’t catch up with the girl’s train. The boy consoles himself with the thought that relative to him, the girl is moving, so her clock is running slow, and at least she won’t have forgotten about him by the time she leaves her train. An hour passes on the boy’s watch. How much time (according to him) has the girl’s watch advanced in that period (assuming they both stay on their trains)?

11.4

An observer on Earth sees two spaceships (or trains, whatever you prefer) approaching from opposite directions. The observer measures their velocities in his/her own rest frame, and not knowing about relativity, uses Galilean velocity addition to conclude that the two spaceships have a relative speed of \((7/5)v\). However, an observer on one of the spaceships measures the relative speed of the other as \((35/37)c\). Find the speeds of the two spaceships relative to the Earth.

11.5

A male and a female student both attend relativity lectures. The boy however is more interested in the girl than in the lecture. Frustrated, the teacher throws a wet sponge towards him, at speed \(c/2\). The girl, hoping to save the boy, tries to intercept the sponge, throwing her marker at it from the side (making a right angle, i.e., coming at the sponge from a direction perpendicular to its direction of motion, as seen in the (stationary) reference frame of the lecture hall) with speed \(c/3\). For a spider who happens to sit on the sponge, what is the measured speed of the marker?

11.6

A spaceship flies away from Earth with speed \(c/3\). After some time a small shuttle departs from the spaceship, in a direction that makes a right angle with that of the main ship, and a speed of \(c/4\), as measured in the rest frame of the main ship. What are the magnitude and direction of the velocity of the shuttle as measured from Earth?

Angles in Lorentz transformations

(a) A rod moves with velocity \(v\) in a straight line relative to an inertial frame \(S\). In its rest frame the rod makes an angle of \(\theta^\prime\) with the forward direction of its motion. Find the angle \(\theta\) the rod appears to make with the direction of motion as measured in the frame \(S\). Determine the numerical value of this angle for \(\theta^\prime=60^\circ\) and \(v=3c/5\).

(b) As observed from an inertial frame \(S\), a mirror is moving with speed \(v\) in the \(x\) direction with its plane surface perpendicular to \(x\). Also as observed in frame \(S\), a photon traveling in the \(xy\)-plane is incident on the mirror surface with an angle \(theta\) to the mirror’s normal. Show that, as seen from \(S\), the reflected photon has an angle \(\bar{\theta}\) with the mirror normal, where

\[\cos \bar{\theta}=\frac{\cos \theta+\cos \alpha}{1+\cos \theta \cos \alpha},\]

and \(\cos\alpha=2(v/c)/(1+(v/c)^2)\).

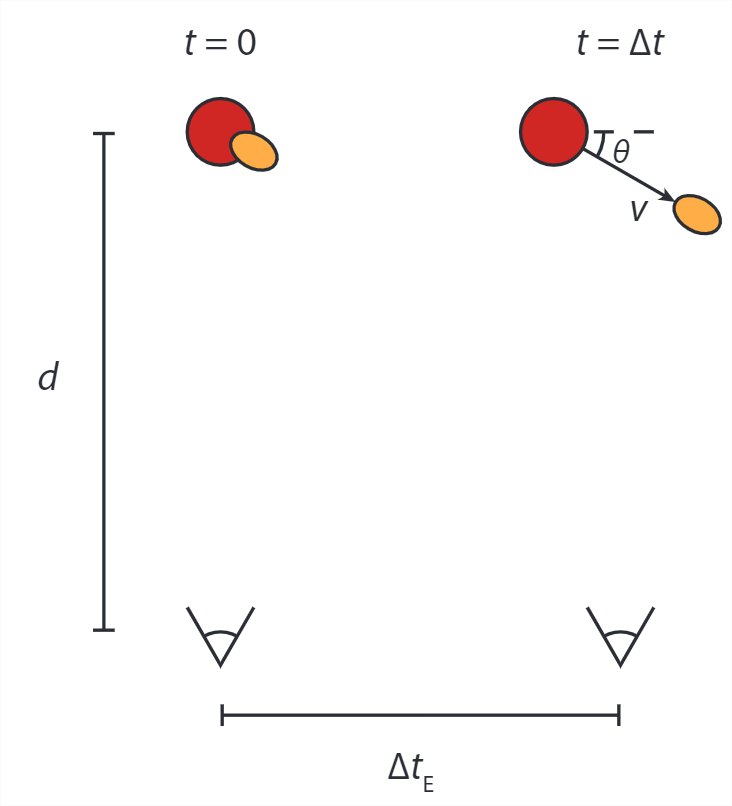
Figure \(\PageIndex{1}\): Observing the explosion of a quasar at large distance.

11.8

Quasars are active galactic nuclei that can emit large amounts of matter, usually gas. Fortunately they are far enough away to never affect us, but close enough that we can measure e.g. the velocity of the emitted gas. These velocities occasionally seem to exceed the speed of light. To see how this can happen, consider a quasar a distance \(d\) away from Earth (as measured in the collective rest frame of the Earth and the quasar), and an explosion on the quasar resulting in such an emission at \(t=0\), see figure \(\PageIndex{1}\). The light emitted at the moment of the explosion reaches Earth at \(t=d/c\). If the emitted gas is moving on a trajectory like the one shown in the figure below, light emitted from the gas has to travel a shorter distance to Earth than the light emitted at the moment of the explosion. Light emitted by an explosion on a distant quasar reaches Earth after a time interval \(d/c\). Light emitted from the expelled gas has to travel a shorter distance. Note that the distance traveled by the gas is much smaller than the distance between Earth and the quasar, so the light arriving from both can be taken as coming from the same direction. Suppose that the gas travels at speed \(v\).

(a) Determine the interval \(\Delta t_E\) between the events ‘Earth observer sees the initial explosion’ (which happens at the quasar at \(t=0\), but is observed later) and 'Earth observer sees the light emitted by the gas at time \(t\)'.

(b) Determine the speed of the gas an Earth astronomer would measure if they don’t take the angle \(theta\) into account (we call this speed \(v_{obs}\)).

(c) Show that the observed velocity can exceed the speed of light.

(d) Show that for given actual velocity \(v\) of the gas, the observed velocity is maximized if \(\sin\theta = v/c\), and that in that case we get \(v_{obs}=\gamma(v)v\).

(e) What is the minimum speed \(v\) for the gas at which it can appear to have a speed equal to that of light?

11.9

[For section 11.4] Prove the last equality in equation (11.4.6) by expanding the hyperbolic tangents in the fraction in exponential functions.

11.10

[For section 11.4] Prove equation (11.4.9) by induction. If this is the first time you prove something by induction: step 1 is to prove that the equation holds for \(n=1\) (completely trivial in most cases); step 2 is to prove that if the equation holds for all values up to \(n\), it also holds for \(n+1\). In this case, you thus have to calculate \(u_{n+1}\) by (relativistically) adding \(u\) and \(u_n\).