13: The Sun
- Page ID
- 31135
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe the properties and composition of the Sun.
- Describe the layers of the solar interior.
- Describe the solar atmosphere.
- Understand the various times of solar weather, including sunspots, solar flares, prominences, and coronal mass ejections.
- Understand the process of nuclear fusion and how it produces the energy emitted from the Sun.
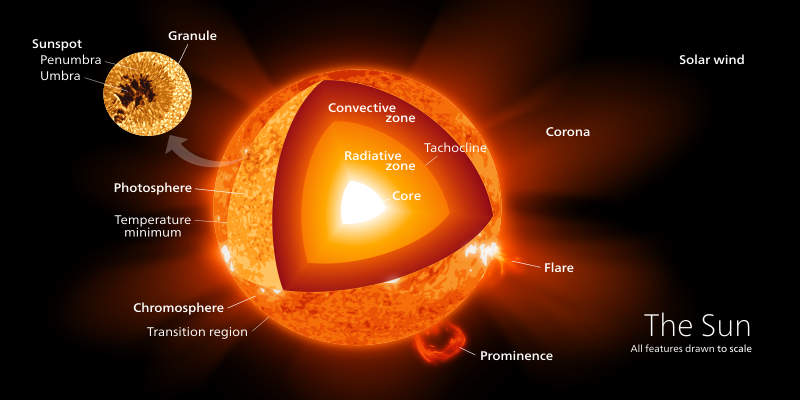
The Sun lies at the heart of the Solar System, containing over 99.9% of the total mass. It is also by far the largest object in the Solar System, with a radius of 6.9X108 m, about 109 times that of the Earth. The Sun is the source of the energy that makes life possible on Earth. But how much energy does it radiate?
We can measure the luminosity, the total energy radiated by the Sun, by measuring the fraction of that energy that reaches Earth. Imagine a sphere with a radius of 1 AU centered on Sun. The amount of energy per unit area the Earth receives would be one fraction of the total energy. Total surface area of this imaginary sphere can be found using the formula 4πr2. Using this area, we can find that the total luminosity is of the Sun is about 3.8 × 1026 W. This is the equivalent of 10 billion 1-megaton nuclear bombs being detonated every second.
Based on our models on the formation of the Solar System, the Sun is about 4.6 billion years old. Based on its mass of 2X1030 kg (300,000 times the mass of the Earth) and its current rate of converting hydrogen into helium, the Sun is about halfway through its life cycle.
By measuring the motion of sunspots, we have determined that the Sun rotates at its equator once every 25.4 days relative to the stars. Since the Earth’s orbital motion is in the same direction as the solar rotation, the Sun rotates every 27.3 days relative to the Earth. Like the Jovian planets, the Sun is a gaseous body without a solid surface, so it rotates differentially. Its equatorial region rotates faster (25 days) than the polar regions (33 days).
The light that reaches the Earth originates in the Sun’s photosphere. Using spectral analysis of this light, we have been able to determine the temperature and composition of the outer layers of the Sun. However, we have no direct means of measuring the Sun’s interior. So, we have to rely on mathematical models. Fortunately, the behavior gases like hydrogen and helium at high temperatures and pressures is well understood by scientists, so by combing modeling with experimentation, we can be confident about the behavior and nature of the solar interior.
Based on analysis and calculations, scientists have determined that the Sun’s composition is as follows:
- Helium - 8.7% of atoms, 27.1% of mass
- Oxygen - 0.078% of atoms, 0.97% of mass
- Carbon - 0.043% of atoms, 0.40% of mass
- Nitrogen - 0.0088% of atoms, 0.096% of mass
- Silicon - 0.0045% of atoms, 0.099% of mass
- Magnesium - 0.0038% of atoms, 0.076% of mass
- Neon - 0.0035% of atoms, 0.058% of mass
- Iron - 0.0030% of atoms, 0.14% of mass
- Sulfur - 0.0015% of atoms, 0.040% of mass
The high temperatures of the Sun free the electrons from their atoms, converting the gas into plasma, the fourth state of matter. Plasma is a lot like gas but is a mixture of charged particles at high temperatures where electrons and nuclei are free to move about.
Two forces act on the Sun. One is the inward gravitational pressure of the Sun’s mass. The other is the outward pressure from heat generated in its interior. The Sun remains stable because these two forces are in gravitational equilibrium. The energy supplied by fusion maintains the pressure that balances the inward crush of gravity. So long as these forces are balance, the Sun will neither shrink nor expand. Should one become stronger than the other, the Sun would become out of balance and its size would change. To maintain the proper energy balance, the rate at which energy radiates from the surface of the Sun must be the same as the rate at which it is released by fusion in the core.
During the early formation of the Solar System, the energy that heated the core came from gravitational contraction. Once the pressures inside the core became high energy to trigger fusion, contraction stopped, and the Sun stabilized.

