3: C3) Vector Analysis
( \newcommand{\kernel}{\mathrm{null}\,}\)
- 3.1: Coordinate Systems and Components of a Vector (Part 1)
- The vector component is the product of the unit vector of an axis with its scalar component along that axis. A vector is the resultant of its vector components. The scalar x-component of a vector can be expressed as the product of its magnitude with the cosine of its direction angle, and the scalar y-component can be expressed as the product of its magnitude with the sine of its direction angle.
- 3.2: Coordinate Systems and Components of a Vector (Part 2)
- In a plane, there are two equivalent coordinate systems. The Cartesian coordinate system is defined by unit vectors i^ and j^ along the x-axis and the y-axis, respectively. The polar coordinate system is defined by the radial unit vector r^, which gives the direction from the origin, and a unit vector t^, which is perpendicular (orthogonal) to the radial direction.
The language of physics is mathematics. This is not just a thing we tell ourselves, but is a basic fact that separates the physical sciences from the social sciences. Although we may speak and write about physics using a spoken and written language (English, in this case), this is just for descriptive convenience. Anytime we actually want to do anything with physics, we have to cast it into mathematics. Part of this is a desire for precision - if I say "the acceleration due to gravity is 9.81 m/s2", I know exactly how precise that number is (typically we assume the uncertainty is in the last decimal point, so that implies ±0.01 m/s2 on that number). However, it's also a necessity, since no amount of words can actually be used to exactly describe any physical law, and words don't inherently have precise meaning. Take even the most basic of physical laws - Newton's first law "An object in motion remains in motion until acted on by an external force." What is "motion"? What does it mean to be "acted on"? What is "force"? No amount of language is going to answer these questions, only mathematics is going to give us careful definitions of these concepts1.
So, once we are convinced that we need to use mathematics to do physics, we know that we need to understand how to associate physics quantities ("mass", "speed", "force") with mathematical variables. In some cases, this is very easy - for example, the temperature of something is just a number, call it T. Or the mass of something is a number m. Single numbers are called scalars. Sometimes these numbers have constraints on them that come from reality - for example, mass must be positive, and temperature has a minimum value (absolute zero). But there are also quantities which need more than just a single variable, or additional conditions on that variable - they actually must carry more information. The most important of these are vectors, which carry both a number (the magnitude, or length of the vector), and a direction.
The length of a vector is a pretty straightforward idea - vectors are arrows, and the size of the arrow is the length. But direction is a little bit more confusing, because it can be specified in several different ways. For example, I can be driving at a speed of 32 mph, in the direction "north". Or maybe in the direction "towards you", or "90∘ from East". Because of this uncertainty, we will often choose to represent vectors using components - that is, an xy-Cartesian coordinate system. Of course, this coordinate system is something we created out of thin air to help us solve the problem, so which coordinate system we pick should not influence our calculation in the slightest.
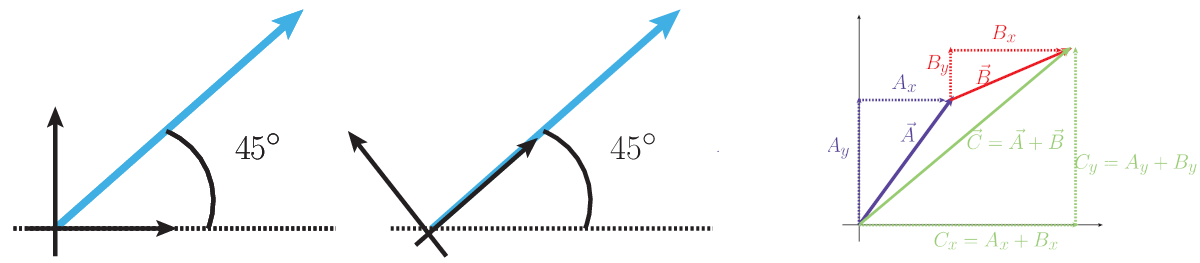
For a concrete example, consider a vector of length 5, that is pointed 45∘ above the horizontal (see the figure on bottom left). We can choose to represent this vector in a number of ways. In a coordinate system fixed to the horizontal, the vector has components
vx=5cos(45)≃3.53,vy=5sin(45)≃3.53.
Alternatively, if you pick a coordinate system with the x-axis along the vector itself (figure on bottom middle), the components would be
vx=5,vy=0.
In some cases one of these might be preferable to the other, but there is something important here: although the coordinate representation changed, the magnitude and direction did not. No choice of coordinate system can change the magnitude and direction of a physical variable like a vector, because coordinates are just helping tools to do physics.
There is one last point to make about vectors in coordinate systems, which is summed up by the last figure: performing mathematics like addition on vectors means the same mathematics applies to the components. This makes working with components very convenient - we don't actually need to go around making pictures of arrows and measuring them, we can just use the components and get the results algebraically.
1If you're interested, the mathematical statement of Newton's first law is something like "→a=0⊃Σ→Fext=0", using the symbol ⊃ for "if".

